【脱・数学アレルギー】AI学習の第一歩!ベクトルと行列の世界へようこそ
みなさんは、AIや機械学習の勉強を始めようとして、参考書を開いた瞬間にそっと閉じた経験はありませんか。わたしはあります。そこには、見慣れない記号や数字の羅列が並んでいるからです。
でも、安心してください。AIエンジニアとして活躍するために、数学者のような厳密な証明ができる必要はありません。大切なのは「それが何を意味しているのか」「どうやって使うのか」というイメージと、それをプログラム(Python)でどう書くかを知ることです。
今回は、E資格の試験範囲「線形代数」の入り口である、スカラー、ベクトル、そして行列について、まったくの初心者の方に向けてお話しします。
なぜAIに数学(線形代数)が必要なのか
そもそも、なぜ私たちはこんな小難しいものを学ばなければならないのでしょうか。
機械学習(Machine Learning)を支えているのは「応用数学」です。その中でも、データをまとめて扱ったり、計算を高速に行ったりするために必須なのが「線形代数学」なのです。
たとえば、画像のデータも、音声のデータも、コンピュータの中ではすべて「数字の羅列」として扱われます。その数字の塊を効率よく処理するための道具が、今日学ぶベクトルや行列だと思ってください。料理をするのに包丁とまな板が必要なように、AIを作るにはベクトルと行列が必要なのです。
スカラーとベクトルの違い
まずは言葉の定義から始めましょう。難しく構える必要はありません。
スカラーとは
スカラーとは、いわゆる「普通の数」のことです。みなさんが普段使っている や
、
などがこれに当たります。これらは「大きさ」だけを表す量です。
もちろん、普通の数ですから、足し算、引き算、掛け算、割り算が可能です。
ベクトルとは
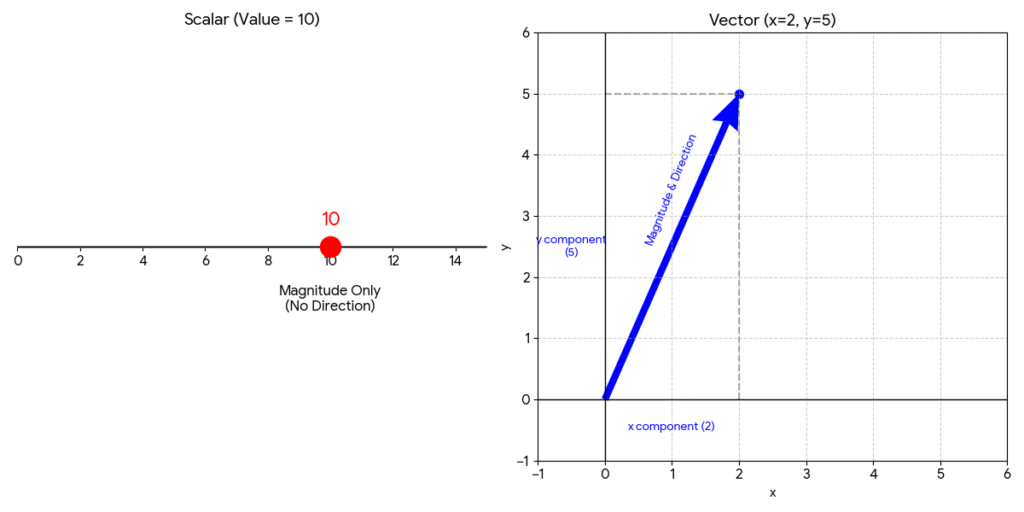
一方で、ベクトルとは何でしょうか。ベクトルは「大きさ」と「向き」を持つものです。よく矢印で図示されるアレです。
でも、データ分析の世界ではもっと単純に「数を一列に並べたセット」と捉えてみてください。
たとえば、ある人の身長が cm、体重が
kgだとします。これを別々に扱うのではなく、
というひとつのセットとして扱う。これがベクトルのイメージです。
Pythonでベクトルを作ってみよう
では、実際にPythonを使って、スカラーとベクトルを作ってみましょう。AI開発の標準ライブラリであるNumPy(ナンパイ)を使います。
import numpy as np
# スカラー(ただの数値)
scalar_value = 10
print("スカラー:")
print(scalar_value)
# ベクトル(数の並び)
# リスト形式で渡すことでベクトルになります
vector_value = np.array([2, 5])
print("\nベクトル:")
print(vector_value)これを実行すると、単なる数字の と、
という並びが表示されます。
この は、座標で言えば「右に
進んで、上に
進む矢印」を表しているとも言えますね。
行列:ベクトルの進化形
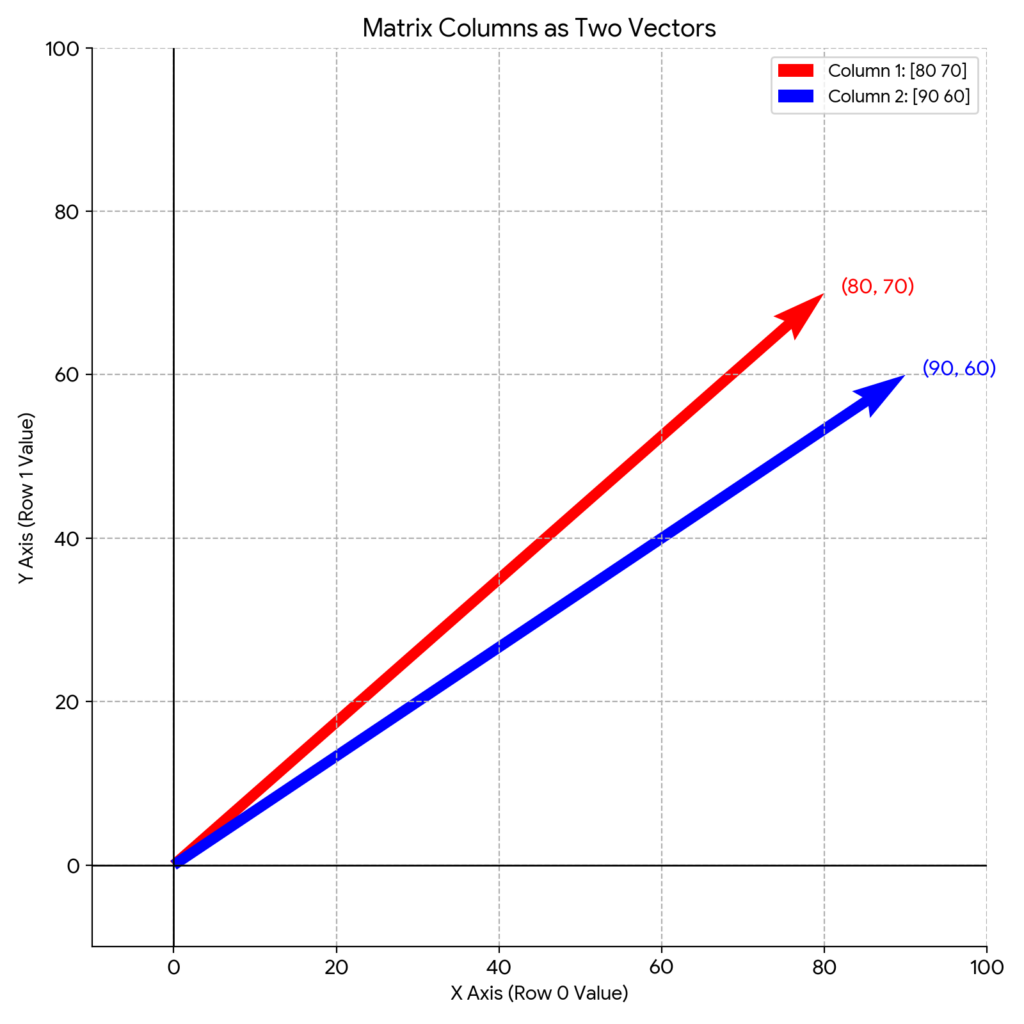
さて、ベクトルが「数を一列に並べたもの」だとすれば、それをさらに「長方形や正方形に並べたもの」が行列です。
「スカラーを表にしたもの」や「ベクトルを並べたもの」ですね。Excelのスプレッドシートのような、縦と横に数字が並んだ表をイメージしてください。
たとえば、数学のテストの点数が 点、英語が
点のA君と、数学
点、英語
点のB君がいるとします。これをまとめて表にするとこうなります。
A君のデータ
B君のデータ
これらを積み重ねて、
としたもの、これが行列です。
行列は何に使うのか
「なんでわざわざそんな書き方をするの」と思いませんか。
実は、行列を使うと、膨大な数の連立方程式を一気に解いたり、画像の変形(回転や拡大)を一瞬で計算したりできるのです。これを「線形変換(1次変換)」と言ったりします。
これからの連載で詳しく解説しますが、行列は「データを変換する装置」あるいは「連立方程式の係数をまとめた箱」だと今は思っておいてください。
Pythonで行列を作ってみよう
では、先ほどのA君とB君の点数データを行列としてPythonで表現してみましょう。
import numpy as np
# 行列(2行2列の例)
# リストの中にリストを入れることで行列を表現します
matrix_value = np.array([
[80, 90],
[70, 60]
])
print("行列:")
print(matrix_value)
# 形状(シェイプ)を確認する
# (行数, 列数) が表示されます
print("\n行列の形:")
print(matrix_value.shape)
コードを見るとわかるように、ベクトルをさらに [ ] で囲むことで行列を作っています。これが「ベクトルのベクトル」という感覚です。
今後の学習の指針
いかがでしたか。
「線形代数」という怖い名前の学問も、蓋を開けてみれば「数字を便利に扱うための表記ルール」に過ぎないことがわかってきたのではないでしょうか。
今日のポイントは以下の3点です。
- スカラーは「普通の数」、ベクトルは「数のセット(向きと大きさ)」
- 行列は「ベクトルを並べた表」
- PythonのNumPyを使えば、これらを簡単にプログラムで表現できる
次回は、いよいよこの行列を使って計算をしてみます。特に「行列の掛け算」は普通の数の掛け算とは少しルールが違います。ここが最初の難関ですが、図解しながら丁寧に解説しますので楽しみにしていてくださいね。
【第2回】行列計算の壁を越えよう!「魔の掛け算」と連立方程式
前回は、AI(人工知能)を理解するための第一歩として、スカラー、ベクトル、行列という言葉の意味と、Pythonでの基本的な作り方を学びましたね。
「なんだ、ただの数字の表じゃないか」
そう思った方もいるかもしれません。しかし、行列の本領発揮はここからです。今日は、多くの初学者が最初に躓く(つまずく)ポイントである「行列の演算」、特に独特なルールを持つ「掛け算」と、それがどのように「連立方程式」に応用されるのかを見ていきましょう。
ここを乗り越えれば、線形代数の基礎の半分はクリアしたも同然です!
足し算と引き算は「直感的」でOK
まずは準備運動です。行列にも普通の数と同じように、足し算と引き算があります。
これは非常にシンプルです。「同じ場所にある数字同士を足す(引く)」 だけです。
たとえば、次の2つの行列を足してみましょう。
簡単ですよね?
左上の と
を足して
。右下の
と
を足して
。これだけです。引き算も全く同じルールです。
ただし、注意点がひとつだけあります。それは 「形が同じ行列同士でないと計算できない」 ということです。 の行列と
の行列を足すことはできません。
最初の難関!「行列の掛け算」のルール
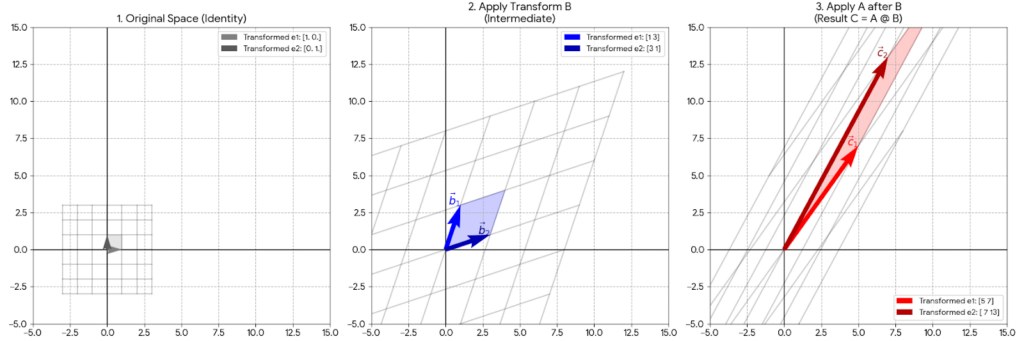
さて、ここからが本番です。行列の掛け算は、足し算のように「同じ場所同士を掛ける」のではありません。ここで行列独特のルールが登場します。
言葉で言うとこうなります。
「左の行列の『行(横)』と、右の行列の『列(縦)』を順番に掛けて足す」
……と言われても、ピンときませんよね。具体的な例を見てみましょう。
ベクトルと行列の積
まずは、行列とベクトル(縦長の行列)の掛け算です。
この計算はどうなるでしょうか?
答えから先に書くとこうなります。
何が起きているか分解してみましょう。
- 上の段(14)を作る:左の行列の「1行目(横)」である
と、右のベクトルの「縦」である
に注目します。先頭同士(
と
)、後ろ同士(
と
)を掛けて、それを足します。
- 下の段(13)を作る:左の行列の「2行目(横)」である
と、右のベクトルの「縦」である
を使います。同様に、
このように、「左側は横に見て、右側は縦に見る」 のが行列の掛け算の鉄則です。結果として、変換後の新しい要素(この場合は14)は、元の要素のすべて(6, 4, 1, 2)から影響を受けて決まることになります。
行列同士の積
行列同士になってもルールは同じです。
これを計算するとどうなるでしょうか?
「左の行」と「右の列」の組み合わせを4回行うことになります。
- 左上: (左の1行目)
(右の1列目)
- 右上: (左の1行目)
(右の2列目)
- 左下: (左の2行目)
(右の1列目)
- 右下: (左の2行目)
(右の2列目)
よって、答えはこうなります。
慣れるまでは指でなぞりながら計算することをお勧めします。「横、縦、掛けて足す!」と唱えましょう。
なぜこんな面倒なことを? 連立方程式との関係
「普通に掛け算させてくれよ!」と言いたくなる気持ち、わかります。でも、この独特なルールのおかげで、連立方程式を驚くほどシンプルに記述できるのです。
中学校で習ったこんな連立方程式を思い出してください。
(ここでは変数を ではなく
と書いています)
この式の「係数(文字の前の数字)」だけを抜き出して行列 を作り、変数
をベクトル
、右辺の数字をベクトル
とすると……
先ほどの掛け算のルールを使って を計算してみましょう。
これと右辺の が等しいということは……
見てください! もとの連立方程式がそのまま再現されましたね。
つまり、あのごちゃごちゃした連立方程式は、行列を使えば
という、たった3文字の式で表せてしまうのです。
これが、機械学習で何百万ものパラメータを持つ巨大な計算を扱う際に、行列が不可欠である理由の一つです。
Pythonで計算してみよう
手計算だと大変な行列の掛け算も、Python(NumPy)なら一瞬です。
NumPyでは、行列の積(ドット積)を計算するために np.dot() 関数か、 @ 演算子を使います。( * を使うと「同じ場所同士の掛け算」になってしまうので注意してください!)
import numpy as np
# 行列 A の定義
A = np.array([
[2, 1],
[4, 1]
])
# 行列 B の定義
B = np.array([
[1, 3],
[3, 1]
])
print("行列 A:")
print(A)
print("\n行列 B:")
print(B)
# 行列の積を計算 (A × B)
# np.dot(A, B) でもOKですが、最近は @ を使うのが主流です
C = A @ B
print("\n行列の積 (A @ B):")
print(C)
これを実行すると、手計算で求めた が一瞬で表示されるはずです。
まとめと次回予告
今回は、少し厄介な「行列の掛け算」と、それを使って「連立方程式」がシンプルに書けることを学びました。
- 行列の足し算・引き算は「同じ場所」同士。
- 行列の掛け算は「左の行」
「右の列」。
- 連立方程式は
という行列の式で表せる。
さて、方程式 が書けたなら、次は「どうやって
(答え)を求めるか」が気になりますよね。
普通の方程式 なら、両辺を
で割って
とすれば解けます。
しかし、行列に「割り算」はありません。
その代わり登場するのが「逆行列(ぎゃくぎょうれつ)」です。
次回は、この「行列の割り算」にあたる概念と、行列の「大きさ」を表す不思議な値「行列式」について解説します。一見難しそうですが、図形の「面積」として捉えると驚くほど直感的に理解できますよ。
【第3回】行列に「割り算」はある?逆行列と「面積」の秘密
前回は、行列の独特な「掛け算」と、それを使って連立方程式を というシンプルな形で表せることを学びましたね。
ここでひとつの疑問が湧いてきませんか?
「掛け算があるなら、割り算はないの?」と。
普通の方程式 なら、両辺を
で割って(つまり
を掛けて)
と解きますよね 。
もし行列でも同じことができれば、 の
を「割る」ことで、一発で正解
が求められそうです。
今回は、行列における割り算の正体である「逆行列(ぎゃくぎょうれつ)」と、それが存在するかどうかを見極める「行列式(ぎょうれつしき)」について解説します。
少し抽象的な話になりますが、「逆数」と「面積」というイメージを持てば、決して難しくありませんよ。
行列の世界の「1」:単位行列
割り算の話をする前に、ひとつだけ覚えておかなければならない特別な行列があります。それは「単位行列(たんいぎょうれつ)」です。
普通の数の計算では、何を掛けても変化しない数字として がありますよね(例:
)。
行列の世界でこの の役割を果たすのが、単位行列です。通常
や
という記号で表されます。
具体的には、左上から右下への対角線上に が並び、それ以外がすべて
であるような行列です。
どんな行列 にこの
を掛けても、結果は
のまま変わりません。
これが、行列界の「1」です。
行列の割り算=「逆行列」を掛けること
さて、本題の割り算です。
厳密には行列に「割り算」という計算はありません。その代わり、「掛けると単位行列(1)になる行列」を使います。
普通の数で考えてみましょう。 を
にするには、何を掛けますか?
そう、逆数の ですよね。
これと同じように、ある行列 に対して、掛け合わせると単位行列
になるような行列のことを、「逆行列」と呼び、
(Aインバース)と書きます 。
つまり、連立方程式 を解くという作業は、両辺の左側からこの
を掛ける作業そのものなのです 。
- 左から
を掛ける
は
(1)になるので消える
- 答えが出る!
このように、逆行列さえ求まれば、面倒な連立方程式の解が一瞬で計算できるわけです。
逆行列はいつでも作れるわけではない?
「じゃあ、どんな行列でも逆行列を作って方程式を解けるんだ!」
……と言いたいところですが、実はそうではありません。
普通の数でも、 で割ること(
)はできませんよね。
それと同じで、行列にも「逆行列が存在しない(割れない)」場合があります 。
ここで登場するのが、「行列式(ぎょうれつしき)」という概念です。英語ではDeterminant(ディターミナント)と呼び、 や
と書きます 。
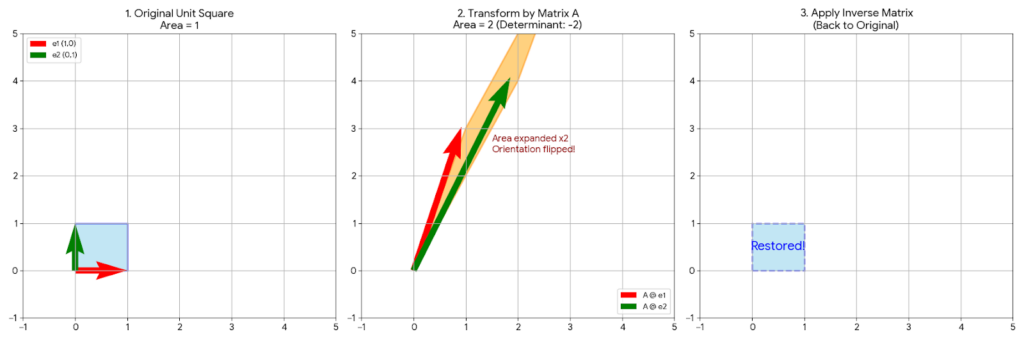
行列式=変換による「面積」の倍率
行列式の正体、それはズバリ「行列が作る平行四辺形の面積(体積)」です 。
行列 を、2つのベクトル
と
のセットだと考えてみましょう。
この2つのベクトルが作る平行四辺形の面積が、行列式の値( )になります 。
もし、この面積が だったらどうなるでしょうか?
面積が ということは、2つのベクトルが同じ方向を向いていて(平行で)、平行四辺形がペチャンコになっている状態です 。
この「ペチャンコになった行列」には、逆行列が存在しません 。
まとめると、こういうことです。
- 行列式
のとき:逆行列が存在する(方程式が解ける)
- 行列式
のとき:逆行列が存在しない(解けない、あるいは解が定まらない)
この判別式のような役割をするから、「行列式(Determinant=決定するもの)」と呼ばれるんですね。
Pythonで逆行列と行列式を計算してみよう
では、Pythonを使って実際に計算してみましょう。
NumPyの linalg (リニア・アルジェブラ=線形代数)というモジュールを使います。
import numpy as np
# 行列 A の定義
A = np.array([
[1, 2],
[3, 4]
])
print("行列 A:")
print(A)
# 1. 行列式 (Determinant) を求める
# det(A) = 1*4 - 2*3 = 4 - 6 = -2 になるはずです
det_A = np.linalg.det(A)
print(f"\n行列式 (det): {det_A:.2f}")
# 2. 逆行列 (Inverse) を求める
# 行列式が 0 でないので、逆行列が存在します
inv_A = np.linalg.inv(A)
print("\n逆行列 A^(-1):")
print(inv_A)
# 3. 検算:A と 逆行列を掛けると単位行列になるか?
# コンピュータの誤差で完全に0や1にならないことがありますが、ほぼ単位行列になります
identity_check = A @ inv_A
print("\n検算 (A @ A^(-1)):")
print(identity_check)
これを実行すると、検算の結果が
に近い形になり、確かに「掛けて1になる」関係が確認できるはずです。
もし、行列式が になるような行列(例えば
など)で
np.linalg.inv() を実行しようとすると、Pythonは「特異行列です(Singular matrix)」といってエラーを出します。これもぜひ試してみてください。
今後の学習の指針
今回は、行列における「割り算」の役割を果たす逆行列と、その存在を判定する行列式について学びました。
- 単位行列:掛け算しても値を変えない「1」のような行列
- 逆行列:掛けると単位行列になる「逆数」のような行列
- 行列式:行列が持つ「面積」。これが0だと逆行列は作れない
これで、基本的な行列の四則演算(足し・引き・掛け・割りっぽいもの)が揃いました!
しかし、AIの学習ではもっと巨大なデータや、複雑な構造を扱います。
次回は、行列のさらに深い性質である「ランク(階数)」や、AI特有の計算である「アダマール積」、そして行列をさらに拡張した概念「テンソル」について解説します。「テンソル」と聞くと難しそうですが、実は皆さんがすでに知っているアレのことなんですよ。
【第4回】行列の「階級」と「テンソル」?AI特有の計算ルール
前回は、行列の「逆行列」と「行列式」についてお話ししました。行列式が「面積」のようなもので、それが になると逆行列(割り算)ができない、という話でしたね。
今回は、その話をもう少し発展させた「ランク(階数)」という概念と、AIの現場では頻繁に登場するけれど学校の数学ではあまり習わない「アダマール積」、そして「テンソル」というカッコいい名前の用語について解説します。
名前はいかついですが、中身はとてもシンプルです。「なんだ、そんなことか」と拍子抜けするかもしれませんよ。
行列の「ランク(階数)」とは?
前回の記事で、「行列式が になると、平行四辺形がペチャンコになって逆行列が存在しない」と言いました。
この「ペチャンコ具合」や「行列が持つ情報の充実度」を表す数字が、ランク(Rank)、日本語では階数(かいすう)です。
データの「重複」を見抜く
たとえば、あるクラスのテスト結果を分析するために、次のような3つのデータ(ベクトル)を集めたとします。
- 国語の点数
- 数学の点数
- 「国語と数学の合計」の点数
この3つのデータを行列にまとめたとしましょう。データは3列ありますが、実は「3. 合計点」は「1」と「2」を足しただけなので、新しい情報は何も増えていませんよね。
この場合、見かけ上の列数は3つでも、実質的に意味のある独立したデータは「2つ」しかありません。
この「実質的に意味のあるデータの数」がランクです。
もし の行列でランクが
なら、フルに情報が詰まっています(これを「フルランク」と呼びます)。
もしランクが や
しかなければ、どこかに重複や無駄があり、行列式は
になります。
AIの学習において、データがきちんと意味を持っているか、無駄な重複がないかを知るために、このランクという概念が役に立つのです。
もうひとつの掛け算「アダマール積」
第2回で、少し複雑な「行列の掛け算(行列積)」を覚えましたよね。「行と列を掛けて足す」あの大変な計算です。
しかし、AI(特にディープラーニング)の世界では、もっと単純な掛け算もよく使います。
それがアダマール積(Hadamard product)、または要素ごとの積(Element-wise product)です。
ルールは簡単です。「同じ場所にある数字同士を、ただ掛けるだけ」。
足し算の掛け算バージョンだと思ってください。記号では や
で書かれることが多いです。
いつ使うの?
画像の特定の部分だけを黒く塗りつぶしたり(マスキング)、ニューラルネットワークの信号調整(ゲート機構)を行ったりするときに使われます。
「行列積」と「アダマール積」、AIプログラミングではこの2つを明確に使い分ける必要があります。
「テンソル」ってなに?
さて、いよいよ「テンソル(Tensor)」です。
SF映画に出てきそうな響きですが、これはスカラー、ベクトル、行列をさらに一般化した呼び名に過ぎません。
データを「数字を入れる箱」だとイメージしてください。
- 0次元テンソル(スカラー): ただの数字。点。
- 1次元テンソル(ベクトル): 数字が一列に並んだもの。線。
- 2次元テンソル(行列): 数字が縦横に並んだもの。面。
- 3次元テンソル: 行列がさらに奥ゆきを持って並んだもの。立方体。
AI、特に画像を扱う場合、この「3次元テンソル」が主役になります。
カラー画像は、 のピクセルに加え、「色(赤・緑・青)」の3層のチャンネルを持っています。つまり、画像データは
という形の3次元テンソルなのです。
さらに、この画像を100枚まとめてAIに学習させる場合、データは という4次元テンソルになります。
このように、次元が増えても統一して扱える便利な言葉が「テンソル」なのです。
行列の「勾配」とAI学習
最後に少しだけ、「勾配(こうばい)」について触れておきます。
AIが賢くなる(学習する)仕組みは、答え合わせをして、間違い(誤差)が小さくなるようにパラメータを少しずつ修正することです。
この「どっちに修正すれば誤差が減るか」を示す矢印が勾配(Gradient)です。
高校数学で習う「微分」の親戚ですが、AIでは変数が何万個もあるため、それらをまとめて行列やテンソルの形で微分を行います。
「誤差というスカラーを、重みという行列で微分して、行列の形の勾配を得る」
今はまだ難しく聞こえるかもしれませんが、第6回あたりで学ぶ知識がつながると、この意味がハッキリ見えてくるはずです。
Pythonでランクとアダマール積、テンソルを体験
では、Pythonで確認してみましょう。特に「普通の行列積」と「アダマール積」の違いに注目してください。
import numpy as np
# 行列 A, B の定義
A = np.array([
[1, 2],
[3, 4]
])
B = np.array([
[10, 20],
[30, 40]
])
# 1. 行列のランク (Rank) を調べる
# np.linalg.matrix_rank を使います
rank_A = np.linalg.matrix_rank(A)
print(f"行列Aのランク: {rank_A}")
# わざとランクを下げた行列を作ってみる
# 2行目が1行目の2倍になっている(情報が重複している)
C = np.array([
[1, 2],
[2, 4]
])
print(f"行列Cのランク: {np.linalg.matrix_rank(C)}")
# 2. 掛け算の違い
# 普通の行列積 (内積) は @ を使う
dot_product = A @ B
print("\n行列積 (A @ B):")
print(dot_product)
# アダマール積 (要素ごとの積) は * を使う
# Pythonでは普通の * がアダマール積になります!ここ重要です!
hadamard_product = A * B
print("\nアダマール積 (A * B):")
print(hadamard_product)
# 3. 3次元テンソルを作ってみる
# (2, 2, 3) のテンソル(例:2x2ピクセルのRGB画像のような構造)
tensor_3d = np.array([
[[1, 2, 3], [4, 5, 6]],
[[7, 8, 9], [10, 11, 12]]
])
print("\n3次元テンソルの形 (shape):")
print(tensor_3d.shape)
print("中身:")
print(tensor_3d)
コードを実行すると、行列積とアダマール積で全く違う結果になることがわかりますね。Pythonで実装する際、この記号の使い分け( @ と * )を間違えるのは「新人あるある」なので、ぜひ覚えておいてください。
まとめと次回予告
今回は、少しマニアックですが実用的な概念を詰め込みました。
- ランク(階数): 行列の中の実質的な情報の量。
- アダマール積: 同じ場所同士を掛ける単純な掛け算。記号は
や
*。 - テンソル: 行列を3次元、4次元へと拡張したデータの入れ物。
ここまでの4回で、行列を使った計算の基礎(足し算、掛け算、逆行列、テンソル操作)はほぼ揃いました。
次回は、線形代数のハイライトであり、データの「本質的な特徴」を抜き出すための最強のツール、「固有値(こゆうち)」と「固有ベクトル」について解説します。
「固有」なんて難しそうな言葉ですが、要するに「その行列の『軸』はどこか?」という話です。これを知ると、データを回転させたり、重要な成分だけを取り出したりできるようになります。
【第5回】行列の「性格」を暴く?固有値と固有ベクトル
前回は、行列のランクやテンソルといった、少し発展的な扱い方についてお話ししました。
さて、今回はいよいよ線形代数の「山場」であり、機械学習を理解する上で避けては通れない最重要コンセプト、「固有値(こゆうち)」と「固有ベクトル」について解説します。
名前だけ聞くと、なんだか難しそうで身構えてしまいますよね。「固有」って何が?と。
でも、これは言い換えるなら「その行列の『本当の性格』や『軸』を見つけること」なんです。
データの中に隠れた「重要な特徴」を抜き出すための鍵が、ここにあります。
行列は「変換装置」である
第1回で、行列は「データを変換する装置」だと言いました。
あるベクトルに行列を掛けると、そのベクトルは向きが変わったり、伸び縮みしたりします。これを「線形変換(1次変換)」と呼びます。
たとえば、ある行列を掛けることで、時計の針のようにベクトルが回転したり、ゴムのようにぐにゅっと引き伸ばされたりするイメージを持ってください。
通常、行列を掛けると、ベクトルの「向き」も「大きさ」も変わってしまいます。
「あっちを向いていた矢印が、こっちを向いて、さらに長くなった」という具合です。
向きが変わらない不思議なベクトル
ところが、どんな行列にも(正方行列であれば)、「行列を掛けても向きが変わらない(あるいは真逆になるだけの)」 特別なベクトルが存在します。
行列という嵐の中で、頑として方向を変えない芯の通ったベクトル。
これが「固有ベクトル(Eigenvector)」です。
そして、向きは変わらないけれど、長さは何倍かになります。
その「長さが何倍になったか(スカラー倍)」という倍率のことを、「固有値(Eigenvalue)」と呼びます。
数式で見てみよう
これを数式で書くと、驚くほどシンプルになります。
行列を 、固有ベクトルを
、固有値を
(ラムダ)とすると、次の関係が成り立ちます。
左辺を見てください。行列 とベクトル
の掛け算(行列積)です。本来なら計算が面倒なやつです。
右辺を見てください。スカラー(ただの数値) とベクトル
の掛け算です。ただの引き伸ばしです。
つまり、固有ベクトル にとって、行列
は、単なる数値
と同じ働きしかしないのです。
複雑な行列を、単純な数値(スカラー)として扱えるようにしてしまう。これが固有値・固有ベクトルの凄いところです。
なぜAIでこれが必要なのか?
「向きが変わらないから何なの?」と思うかもしれません。
しかし、この概念はデータの「圧縮」や「特徴抽出」で絶大な威力を発揮します。
たとえば、皆さんの手元に大量のデータ(高次元の点群)があるとします。そのデータがどの方向に広がっているかを知りたいとします。
このとき、データの分散が最も大きい方向(一番情報が詰まっている方向)こそが、固有ベクトルに対応するのです。
これを応用したのが「主成分分析(PCA)」という手法です。
何百個もの項目があるデータから、本当に重要な数個の「主成分(固有ベクトル)」だけを取り出して、データを何十分の一にも圧縮する。AIの前処理でよく行われるこの作業の裏側では、今日学ぶ固有値計算が行われているのです。
行列の対角化
固有値と固有ベクトルがわかると、「対角化(たいかくか)」 という技が使えるようになります。
対角化とは、行列を「対角行列(左上から右下の対角線上にしか数字がない行列)」に変形することです。
対角行列は計算がとても楽です。掛け算をしても、ただ対角線の数字を掛けるだけになるからです。
乗のような計算も、対角化してしまえば一瞬で終わります。
複雑な行列 を、扱いやすい対角行列に変身させるための魔法の杖、それが固有ベクトルなのです。
Pythonで「性格診断」してみよう
では、Pythonを使って行列の固有値と固有ベクトルを求めてみましょう。
ここでもNumPyの linalg モジュールが大活躍します。 eig (アイグ)という関数を使います。
import numpy as np
# 行列 A の定義
# ここでは簡単な 2x2 行列を使います
A = np.array([
[1, 2],
[2, 1]
])
print("行列 A:")
print(A)
# 固有値 (eigenvalues) と 固有ベクトル (eigenvectors) を計算
# w に固有値、v に固有ベクトルが入ります
w, v = np.linalg.eig(A)
print("\n固有値 (lambda):")
print(w)
print("\n固有ベクトル (v):")
print(v)
実行結果を見ると、固有値が2つ(例: と
など)と、それに対応するベクトルが表示されます。
ここで注意点がひとつあります。
Pythonが出力する固有ベクトルは、通常「長さが1」になるように調整(正規化)されています。
また、 v の表示は「縦ベクトルが横に並んでいる」状態です。 v[:, 0] が1つ目の固有ベクトル、 v[:, 1] が2つ目……という見方をするので気をつけてください。
検算してみよう
本当に になっているか、Pythonで確かめてみましょう。
# 1つ目の固有値と固有ベクトルを取り出す
lambda_1 = w[0]
vec_1 = v[:, 0]
# 左辺: A @ x
left_side = A @ vec_1
# 右辺: lambda * x
right_side = lambda_1 * vec_1
print("\n--- 検算 ---")
print(f"左辺 (A @ x): {left_side}")
print(f"右辺 (λ * x): {right_side}")
ほぼ同じ値が表示されたはずです。
行列 を掛けたはずなのに、結果は単に数字(
)を掛けたのと同じになっている。この感動を味わってください!
今後の学習の指針
今回は、行列の核心部分である「固有値・固有ベクトル」について学びました。
- 固有ベクトル:行列を掛けても向きが変わらない特別なベクトル(その行列の「軸」)
- 固有値:そのときベクトルが何倍に伸び縮みするか(その軸の「重要度」)
- 対角化:固有ベクトルを使って、行列を扱いやすい形に変形すること
これで、正方形の行列(正方行列)についての分析手法はかなり整いました。
しかし、世の中のデータはいつも「行と列の数が同じ(正方形)」とは限りません。縦長だったり横長だったりするデータの方が多いでしょう。
そんな「正方形じゃない行列」でも、固有値分解のように成分を分解できる便利な方法はないのでしょうか?
あります。それが次回、最終回で取り上げる「特異値分解(SVD)」です。
画像圧縮や推薦システム(レコメンド)でも使われる、線形代数のラスボス的な存在です。ここまで来た皆さんならきっと理解できるはずです。
【最終回】長方形の行列も分解せよ!特異値分解(SVD)とデータの圧縮
これまで全5回にわたり、AIに必要な線形代数の基礎を一緒に学んできました。
ベクトルから始まり、行列の掛け算、逆行列、そして前回は「行列の性格」を見抜く固有値・固有ベクトルまで到達しましたね。
いよいよ今回が最終回です。
最後にお話しするのは、線形代数のラスボスとも言える「特異値分解(とくいちぶんかい)」、英語でSVD(Singular Value Decomposition)と呼ばれる手法です。
前回学んだ「固有値分解(対角化)」は、とても強力なツールでしたが、弱点がひとつありました。それは「正方形の行列(正方行列)にしか使えない」ということです。
しかし、現実世界のデータは、縦と横の長さが違う「長方形」の行列であることがほとんどです。
「長方形のデータでも、固有値みたいに成分を分解して、重要な特徴だけ取り出したい!」
そんなわがままを叶えてくれる魔法、それが特異値分解(SVD)です。
正方形じゃなくても分解できる魔法
前回の復習ですが、正方行列 は、固有ベクトルを集めた行列
と、固有値を並べた対角行列
を使って、次のように分解できました。
これに対し、どんな形( 行
列)の行列
であっても、次の3つの行列の掛け算に分解できるというのがSVDの主張です。
急に記号が増えて戸惑うかもしれませんが、それぞれの役割は明確です。
(左特異ベクトル):データの「行」方向の特徴を表す正方行列。
(シグマ・特異値):対角線上に「特異値」という数字が並んだ行列。それ以外は
。
(右特異ベクトル):データの「列」方向の特徴を表す正方行列。
ここで一番重要なのが、真ん中にある (特異値) です。
特異値=情報の重要度
この の対角線には、「特異値」と呼ばれる正の数が、大きい順(重要度順)に並んでいます。
これは前回の「固有値」の親戚のようなものです。
- 特異値が大きいほど、その成分は元のデータにとって「重要」である。
- 特異値が小さい(あるいは
に近い)成分は、元のデータにとって「誤差」や「ノイズ」のようなもので、あまり重要ではない。
ということを表しています。
データの「圧縮」への応用
SVDがAIやデータ分析で重宝される最大の理由は、この「重要度順に並んでいる」という性質のおかげです。
もし、行列 を完璧に復元したければ、すべての特異値を使う必要があります。
しかし、「だいたいの形が合っていればいいから、データ量を減らしたい」と思ったらどうすればいいでしょうか?
答えはシンプルです。「小さな特異値を無視して、大きな特異値だけを使って計算し直す」のです。
たとえば、100個の特異値があるデータのうち、上位の10個だけを残して、残り90個を にしてしまいます。
そして の計算をし直すと、元の行列
に非常によく似た、しかしデータ量が圧倒的に少ない行列
ができあがります。
これを「低ランク近似」と呼びます。
画像の圧縮や、ノイズの除去、おすすめ商品を表示するレコメンドシステムなどは、この仕組み(あるいはこれに似た考え方)を使って、「本質的な情報」だけを抽出しているのです。
PythonでSVDを体験しよう
それでは、Pythonで特異値分解を行ってみましょう。
今回は、正方形ではない「長方形」の行列を用意して、それを分解・復元してみます。
import numpy as np
# 正方形ではない行列 (3行4列) を定義
A = np.array([
[1, 2, 3, 4],
[5, 6, 7, 8],
[9, 10, 11, 12]
])
print("元の行列 A:")
print(A)
# 特異値分解 (SVD) を実行
# u: 左特異ベクトル
# s: 特異値 (ベクトルとして返ってきます)
# vh: 右特異ベクトル (転置済み)
u, s, vh = np.linalg.svd(A)
print("\n--- 分解結果 ---")
print("特異値 (Sigma):")
print(s)
# 特異値を使って元の行列を復元してみる
# s はベクトルなので、対角行列に変換する必要があります
Sigma = np.zeros((3, 4))
Sigma[:3, :3] = np.diag(s)
# A_reconst = U @ Sigma @ V^T
A_reconst = u @ Sigma @ vh
print("\n--- 復元した行列 ---")
print(A_reconst)実行結果の「特異値」を見てください。
おそらく、1つ目の数字が非常に大きく、2つ目以降は急激に小さくなっているはずです。
これは、「この行列の情報の大半は、最初の成分に集約されている」ということを意味しています。
もし興味があれば、一番小さな特異値を に書き換えてから復元してみてください。ほとんど元の数字と変わらない結果になるはずですよ。
連載のまとめと、E資格への道
全6回にわたる「ゼロから学ぶ線形代数」、いかがでしたでしょうか。
- ベクトルと行列:ただの数の並びだと知りました。
- 行列の積:「行
列」のルールと連立方程式への応用を学びました。
- 逆行列と行列式:行列の「割り算」と「面積」の関係を理解しました。
- ランクとテンソル:情報の重複や、AI特有のデータ構造に触れました。
- 固有値分解:行列の「軸」を見つけました。
- 特異値分解 (SVD):どんな行列でも分解して、データを圧縮できることを学びました。
これらはすべて、E資格のシラバスにある重要なキーワード です。
最初は何の呪文かと思っていた数式も、今なら「ああ、データの形を変えたり、特徴を取り出したりしているんだな」とイメージできるはずです。
次のステップ
数学の基礎固めが終わったら、次は実際にこれらを使って機械学習のアルゴリズム(回帰分析やニューラルネットワーク)を動かす段階です。
Pythonのコードを書きながら、「あ、ここで内積を使っているな」「ここで勾配を計算しているな」と意識してみてください。理解度が段違いに深まります。
数学は、AIという魔法を使うための「杖」です。
使いこなせるようになれば、作れるものの幅が無限に広がります。
皆さんのE資格合格、そしてエンジニアとしての飛躍を心から応援しています。