ダミー変数とは?
ダミー変数について説明します。少し難しいように聞こえるかもしれませんが、例を使ってわかりやすく解説しますので、安心してくださいね。
ダミー変数とは?
ダミー変数は、統計分析や機械学習で使用される手法の一つです。具体的には、カテゴリカルデータ(カテゴリーに分かれたデータ)を数値データに変換するための方法です。カテゴリカルデータとは、例えば「性別」や「地域」など、値がカテゴリーで表されるデータのことです。
例えば、あるアンケートで「性別」という質問があり、選択肢が「男性」と「女性」の2つだったとします。これをそのまま統計モデルに使うことはできないため、「男性」を1、「女性」を0のように数値に変換します。この変換後の変数がダミー変数です。
なぜダミー変数が必要なのか?
「性別」のようなカテゴリカルデータをそのまま数値データとして扱うと、意味のない計算が行われる可能性があります。例えば、「男性」と「女性」を数値の1と2として扱った場合、2(女性)は1(男性)の2倍だという意味のない解釈が生まれてしまいます。これは統計的に正しくありません。
このような問題を避けるため、ダミー変数を使ってカテゴリカルデータを0と1で表現し、モデルに正しく組み込むのです。
ダミー変数の具体例
具体例を見てみましょう。以下の表は、性別と職業に関するデータです。
| ID | 性別 | 職業 |
|---|---|---|
| 1 | 男性 | エンジニア |
| 2 | 女性 | デザイナー |
| 3 | 男性 | エンジニア |
| 4 | 女性 | マーケティング |
| 5 | 男性 | デザイナー |
このデータを機械学習モデルで扱いたい場合、性別や職業をそのままでは使えないため、ダミー変数に変換します。
まず、性別をダミー変数に変換します。
| ID | 性別(男性=1, 女性=0) | 職業 |
|---|---|---|
| 1 | 1 | エンジニア |
| 2 | 0 | デザイナー |
| 3 | 1 | エンジニア |
| 4 | 0 | マーケティング |
| 5 | 1 | デザイナー |
次に、職業もダミー変数に変換します。職業には3つのカテゴリ(エンジニア、デザイナー、マーケティング)があるので、それぞれにダミー変数を割り当てます。
| ID | 性別(男性=1, 女性=0) | デザイナー | マーケティング |
|---|---|---|---|
| 1 | 1 | 0 | 0 |
| 2 | 0 | 1 | 0 |
| 3 | 1 | 0 | 0 |
| 4 | 0 | 0 | 1 |
| 5 | 1 | 1 | 0 |
このようにダミー変数を使うことで、性別や職業といったカテゴリカルデータを数値データとしてモデルに取り込むことができます。
なお、上記の表にエンジニアの列が含まれていないことに気づかれた方もいらっしゃるかもしれません。
実は、ここではエンジニアを参照グループとして扱っているのです。
参照グループに関しては後ほど詳しく解説しますが、ここでも簡単に説明すると、その名の通り参照グループとは他のグループの比較の参照にするグループのことです。
ダミー変数のメリットとデメリット
メリット
- 解釈が容易になる: カテゴリカルデータを数値化することで、統計モデルや機械学習モデルでの解釈が容易になります。
- モデルの精度向上: 数値データとして扱えるため、モデルの精度が向上する可能性があります。
デメリット
- 次元の増加: カテゴリの数が増えると、その分ダミー変数も増えるため、データの次元が高くなりやすいです。これにより、モデルが複雑になり、処理時間が増えることがあります。
- 情報の一部が失われる: 例えば、「男性」と「女性」だけでなく「その他」というカテゴリがあった場合、2つのダミー変数にすると「その他」の情報が失われることになります。
カテゴリカルデータをダミー変数に変換する際、参照グループを設定することが一般的です。これにより、ダミー変数の数を減らし、モデルの解釈をより明確にします。次に、この参照グループについて詳しく説明し、その影響がどのように重回帰分析の結果に現れるのかについてもお話しします。
参照グループとは?
参照グループ(reference group)とは、カテゴリカルデータの一つのカテゴリを基準として選び、そのカテゴリをダミー変数に含めないことです。この基準となるカテゴリと他のカテゴリとの比較を行うために、残りのカテゴリをダミー変数として設定します。
例えば、先ほどの職業の例では「エンジニア」、「デザイナー」、「マーケティング」の3つのカテゴリがありました。この中で「エンジニア」を参照グループとして設定する場合、「デザイナー」と「マーケティング」の2つのダミー変数を作成します。
| ID | 性別(男性=1, 女性=0) | デザイナー | マーケティング |
|---|---|---|---|
| 1 | 1 | 0 | 0 |
| 2 | 0 | 1 | 0 |
| 3 | 1 | 0 | 0 |
| 4 | 0 | 0 | 1 |
| 5 | 1 | 1 | 0 |
この場合、「エンジニア」の値は自動的に推測されます。すなわち、どちらのダミー変数も0の場合、その観測値は「エンジニア」となります。
参照グループの影響
重回帰分析での参照グループの役割
参照グループは重回帰分析において重要な役割を果たします。重回帰分析では、ダミー変数が独立変数の一部として使われますが、このとき、参照グループは基準として機能し、他のダミー変数の係数がその基準からの差異を表すようになります。
例えば、以下のような重回帰モデルを考えてみましょう。
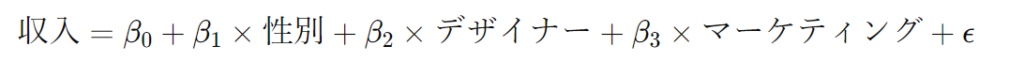
このモデルでの解釈は以下のようになります:
- β0: 「エンジニア」(参照グループ)における基準収入
- β2: 「デザイナー」と「エンジニア」の収入の差
- β3: 「マーケティング」と「エンジニア」の収入の差
つまり、ダミー変数の係数は、参照グループに対して他のグループがどれだけ異なるかを示します。したがって、参照グループそのものの影響は、モデルの定数項(β0)に反映されることになります。
結果の解釈
参照グループを設定することで、分析結果はより解釈しやすくなります。例えば、先ほどのモデルでβ2が5000だった場合、これは「デザイナー」の平均収入が「エンジニア」より5000円多いことを示します。同様に、β3が-3000だった場合、「マーケティング」の平均収入は「エンジニア」より3000円少ないことになります。
これにより、各カテゴリの相対的な位置づけが明確になり、モデルの解釈が容易になるのです。
まとめと今後の学習指針
ダミー変数は、カテゴリカルデータを数値データに変換する重要な手法です。この手法を理解することで、より複雑なデータセットを適切に処理し、精度の高いモデルを作成できるようになります。今後、他の前処理技術や、ダミー変数を使った具体的なモデルの構築方法について学ぶと、さらに理解が深まるでしょう。
投稿者プロフィール


