不偏標準偏差とは？

不偏標準偏差（ふへんひょうじゅんへんさ、Unbiased Standard Deviation）とは、サンプルデータを用いて母集団の標準偏差を推定する際に、サンプルの標準偏差に対してバイアス（偏り）を補正したものです。不偏標準偏差を使うことで、限られたサンプルからでも、より正確に母集団の標準偏差を推定できます。

標準偏差と不偏標準偏差の違い

通常の標準偏差（標本標準偏差）は、データの分散を計算する際に、サンプルデータの平均からの偏差の平方の平均を取ります。しかし、サンプル標準偏差をそのまま使うと、母集団全体の標準偏差を少し過小評価してしまうことが知られています。これを補正するために使われるのが「不偏標準偏差」です。

通常の標本標準偏差の計算式

標本標準偏差 s は、以下の式で計算されます。

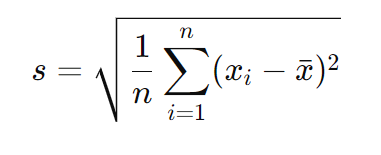
ここで、

この計算方法では、サンプル数 nで割って分散を求めますが、この分散は母集団の分散の推定としてはわずかに低く見積もられてしまいます。

不偏標準偏差の計算式

不偏標準偏差は、分母を n−1で割ることでバイアスを補正しています。

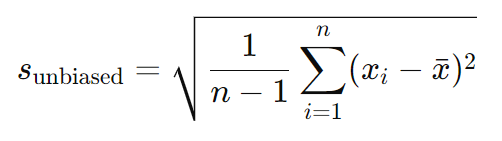
この計算式では、分母が n−1となっており、これを「自由度（Degrees of Freedom）」と呼びます。分母を nから n−1に変更することで、サンプルから計算された標準偏差が母集団の標準偏差に対して過小評価されないようにしています。

なぜ n−1n-1n−1 で割るのか？

サンプルの標準偏差を計算する際、サンプルの平均を使っています。この平均はサンプルから計算されるため、真の母集団平均 とは異なり、サンプル内におけるばらつきを少し小さく見積もる傾向があります。そのため、分母を n から n−1にすることで、この偏りを補正し、より正確な母集団の標準偏差の推定値を得ることができます。

不偏標準偏差の意義と用途

不偏標準偏差は、統計分析において非常に重要です。特に、サンプルデータから母集団の特性を推定する場合、不偏標準偏差を用いることで、より正確な推定が可能になります。以下のような場合に役立ちます。

• 母集団の標準偏差の推定: 母集団全体を調査するのが難しい場合、サンプルから不偏標準偏差を計算して母集団の標準偏差を推定します。
• 推測統計: 信頼区間や仮説検定において、不偏標準偏差が利用されます。

まとめと今後の学習の指針

不偏標準偏差は、サンプルデータから母集団の標準偏差を推定する際に、バイアスを補正した標準偏差です。これを使用することで、サンプルデータが持つ限られた情報からでも、より正確に母集団の分布のばらつきを捉えることができます。統計分析において、不偏標準偏差の理解と適用は、正確なデータ分析の基盤となります。

投稿者プロフィール

山崎講師代表取締役

セイ・コンサルティング・グループ株式会社代表取締役。
岐阜県出身。
2000年創業、2004年会社設立。
IT企業向け人材育成研修歴業界歴20年以上。
すべての無駄を省いた費用対効果の高い「筋肉質」な研修を提供します！
この記事に間違い等ありましたらぜひお知らせください。

最新の投稿

• 新人エンジニア研修講師2024年12月26日研修後のフォローアップメールをより効率的かつ効果的に活用するための「テンプレート作成のポイント」
• 新人エンジニア研修講師2024年12月26日研修講師がフォローアップメールを活用するには？
• 全ての社員2024年12月26日TOEIC 900点レベルの英熟語200選
• 全ての社員2024年12月26日TOEICで頻出する複合名詞（Compound Nouns）