T検定とは?
統計学の世界には、データを分析し、結論を導き出すためのさまざまな手法が存在します。その中でも、「T検定」という方法は非常に広く使われている手法の一つです。では、T検定とは一体何なのでしょうか?
T検定の基本的な考え方
T検定とは、2つのグループの平均値が統計的に異なるかどうかを判断するための統計手法です。たとえば、ある薬の効果を検証する場合に、薬を飲んだグループとプラセボ(偽薬)を飲んだグループの平均値を比較して、その差が偶然によるものか、それとも薬の効果によるものかを判定する際に使われます。
どうして「T検定」という名前なのか?
「T検定」の「T」は、「T分布」という統計分布に基づいていることから来ています。T分布は、サンプルサイズが小さい場合に、正規分布に近い形状を持つ分布です。この分布を利用することで、小規模なサンプルからでも有意な結論を引き出すことが可能です。
T分布のグラフ
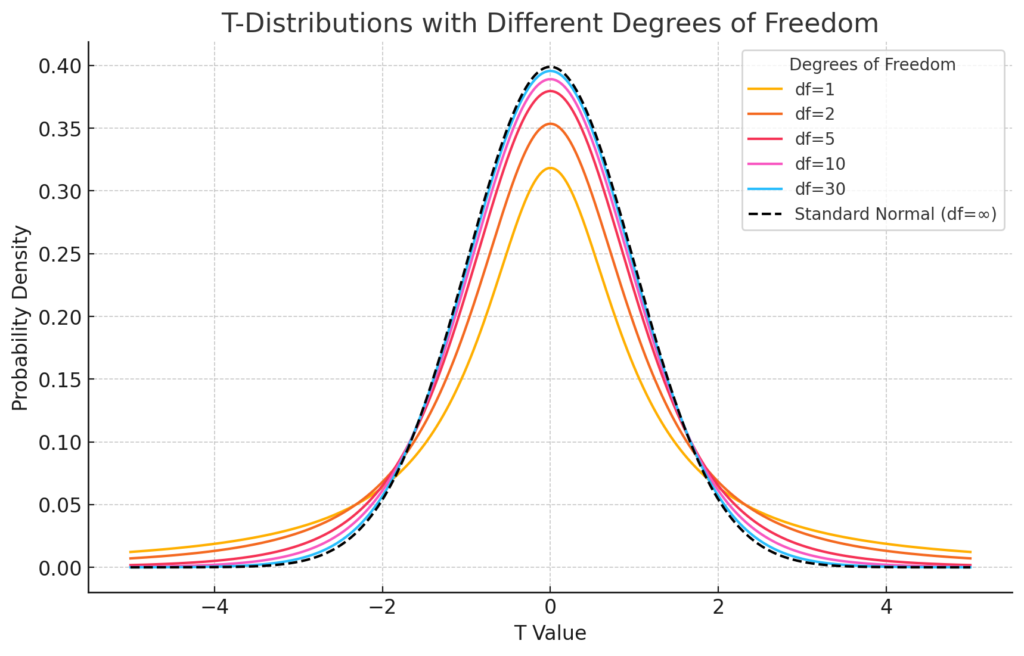
自由度を変化させたときのT分布のグラフです。標準正規分布(自由度が無限大のときのT分布)と比較することで、T分布の特性がよくわかります。
- 自由度が小さいと、T分布は中央が広く、尾が厚くなり、より広がりがあります。これは、データのばらつきが大きくなることを意味します。
- 自由度が増えるにつれて、T分布は標準正規分布に近づいていきます。自由度が30程度になると、ほぼ標準正規分布と見分けがつかないほどになります。
このグラフから、T分布はサンプルサイズが小さいときに正規分布に比べて不確実性が大きいことを表しており、自由度が増える(すなわち、サンプルサイズが大きくなる)と正規分布に収束する特性が視覚的に確認できます。
前提条件
T検定(t-test)は、平均値の比較を行うための統計的手法ですが、適切な結果を得るためにはいくつかの前提条件があります。以下に、T検定で前提とされる主な条件を挙げます。
1. 正規分布
- T検定は、データが正規分布に従っていることを前提としています。これは特にサンプルサイズが小さい場合に重要です。サンプルサイズが大きい場合(一般的には30以上)、中心極限定理により正規性が多少緩和されることもありますが、正規性は依然として重要な前提です。
2. 独立性
- データの各観測値が互いに独立していることが前提です。つまり、一つの観測値が他の観測値に影響を与えないことが条件となります。
3. 等分散性(等分散性の仮定)
- 対応のない二群間のT検定(独立標本T検定)では、二つのグループの分散が等しい(等分散性)ことが前提とされています。この前提が満たされない場合、ウェルチのt検定(分散が等しくない場合に使用するt検定)を用いることが推奨されます。
4. スケール水準
- T検定は、従属変数が連続変数(例えば、比率尺度や間隔尺度)であることを前提としています。従属変数が名義尺度や順序尺度の場合、T検定は適切ではありません。
5. データの代表性
- サンプルデータが母集団の代表であることが前提です。つまり、サンプルが無作為に抽出されていることが重要です。サンプルの結果が母集団に一般化できるようになります。
6. 片側検定と両側検定
- 片側検定(one-tailed test)と両側検定(two-tailed test)についての事前の仮定が明確である必要があります。仮説検定の方向性が適切に設定されます。
T検定の種類
T検定にはいくつかの種類があり、目的やデータの特性によって使い分けられます。主な種類は次の通りです。
1. 対応のあるT検定(Paired T-test)
対応のあるT検定は、同じ対象から得られた2つのデータセットを比較する際に使用します。たとえば、ある学生が試験前と試験後に受けた成績を比較する場合に用いられます。この検定では、同じ人や対象が繰り返し測定されるため、データ間に自然な対応関係があることが前提となります。
2. 対応のないT検定(Independent T-test)
対応のないT検定は、異なるグループ間での平均値を比較する際に使います。たとえば、異なるクラスの学生の試験成績を比較する場合がこれに当たります。この検定では、比較するグループが独立している(相互に影響しない)ことが前提です。
3. 片側T検定と両側T検定
T検定には「片側」と「両側」の2つのバージョンがあります。片側T検定は、ある特定の方向(例えば、「グループAの平均がグループBの平均よりも大きい」)での差を検証します。一方、両側T検定は、差がどちらの方向にあるかに関係なく、単に「差があるかどうか」を検証します。
T検定と自由度
T分布の自由度(degrees of freedom, df)の求め方は、主に次のような状況に応じて異なります。
1. 独立2標本T検定の場合
独立した2つのグループの平均値を比較する際のT検定では、自由度は以下のように計算されます。
自由度の計算式
自由度=n1+n2−2
ここで、n_1は1つ目のグループのサンプルサイズ、n_2は2つ目のグループのサンプルサイズです。
例
もし、グループ1のサンプルサイズが15、グループ2のサンプルサイズが20である場合、自由度は次のようになります:自由度=15+20−2=33
2. 対応のあるT検定の場合
対応のあるT検定(ペアT検定)では、同じ被験者に対して2つの条件で測定を行った場合など、対応するペアのデータ間で平均値の差を検定します。この場合の自由度は以下のように計算されます。
自由度の計算式
自由度=n−1
ここで、nはペアの数(対応するデータの数)です。
例
もし、10人の被験者に対して前後で測定を行った場合、自由度は次のようになります:自由度=10−1=9
3. 一標本T検定の場合
1つのグループの平均値が特定の値と異なるかどうかを検定する一標本T検定の場合、自由度は以下のように計算されます。
自由度の計算式
自由度=n−1
ここで、nはサンプルサイズです。
例
もし、20人のデータを使用して平均を検定する場合、自由度は次のようになります:自由度=20−1=19
自由度の解釈
T分布の自由度は、主にサンプルサイズに依存し、自由度が大きくなるとT分布は標準正規分布に近づきます。自由度が小さいとT分布は尾が厚くなり、極端な値を取りやすくなります。これは、サンプルサイズが小さいと推定の不確実性が大きくなることを反映しています。
T検定を行う際には、正確な自由度を計算し、それに基づいて適切なT分布を使用することが重要です。
T検定のメリットとデメリット
T検定には、次のようなメリットとデメリットがあります。
メリット
- シンプル: T検定は比較的簡単に理解でき、使いやすい手法です。少ないデータでも適用可能であるため、研究の初期段階で非常に役立ちます。
- 強力な仮定: 正規分布に近いデータであれば、非常に強力な検定結果を得ることができます。
デメリット
- 正規性の仮定: データが正規分布に従っているという仮定が前提となっているため、この仮定が崩れると検定結果が信頼できないものになる可能性があります。
- 複数比較の問題: 複数のT検定を同時に行うと、偶然による誤差が蓄積し、誤った結論に至るリスクが高まります。
具体例で考えてみましょう
例えば、あるクラスで新しい学習方法を導入したとしましょう。その効果を確かめるために、新しい方法を試したグループと従来の方法で学んだグループのテスト結果を比較することにします。このとき、T検定を使って両グループの平均点を比較し、その差が統計的に有意であるかどうかを判断することができます。もし結果が有意であれば、「新しい学習方法は従来の方法よりも効果的である」と結論づけることができるわけです。
T検定の今後の学習の指針
T検定は非常に基本的でありながらも強力なツールです。しかし、実際に使いこなすためには、データの前提条件や適用する際の注意点をしっかりと理解することが重要です。次のステップとしては、実際にT検定を行うためのソフトウェア(例えば、ExcelやR、Pythonなど)を使ってみることや、より高度な統計手法(例えば、ANOVAや回帰分析)に進むことが考えられます。
統計学は広範な分野で応用されており、T検定を理解することはその第一歩です。今後もさまざまなデータ分析の手法に触れることで、より深い理解と応用力を身につけていきましょう。
投稿者プロフィール


