【脱・数学アレルギー】AIは巨大な「関数」だ!極限と関数の基礎
前回までの線形代数で、データの扱い方(ベクトルや行列)を学びました。
今回からは、そのデータを使ってAIがどのように答えを導き出すのか、その「仕組み」の部分に入っていきます。その主役が「関数(かんすう)」と「微分(びぶん)」です。
「関数」と聞くと、中学校で習った を思い出して頭が痛くなるかもしれません。
でも、AIエンジニアの視点で見ると、関数は「魔法の箱」に見えてくるはずです。
今回は、微分の手前にある基礎知識、「関数」と「極限(きょくげん)」について、Pythonを動かしながら楽しく学んでいきましょう。
関数とは「変換装置」である
まず、言葉の定義をアップデートしましょう。
数学の教科書には難しいことが書いてあるかもしれませんが、関数とはシンプルに「入力を出力に変換する装置」のことです。
イメージしてください。
ここに「自動販売機」があります。
コイン(入力)を入れると、ジュース(出力)が出てきます。
この自販機こそが関数 です。
数式で と書くとき、それぞれの役割はこうなります 。
:入力(材料、コイン)
:変換装置(自販機、工場)
:出力(製品、ジュース)
AI(人工知能)も、実はこの巨大な関数そのものなのです。
「画像データ(入力)」を入れると、「猫です(出力)」と答える装置。これがAIです。
Pythonで関数を作ってみよう
Pythonでは、その名の通り def (define) を使って関数を定義します。
「入力した数字を2倍にして、1を足す装置」を作ってみましょう。
def my_function(x):
# 入力 x を受け取り、計算して y を返す
y = 2 * x + 1
return y
# 装置を使ってみる
input_data = 3
output_data = my_function(input_data)
print(f"入力: {input_data}")
print(f"出力: {output_data}")
これを実行すると、入力 に対して出力
が返ってきます。これが関数の基本動作です。
「線形」と「非線形」の違い
関数にはいろいろな種類がありますが、AIの世界では大きく2つに分類することがあります。「線形(せんけい)」と「非線形(ひせんけい)」です 。
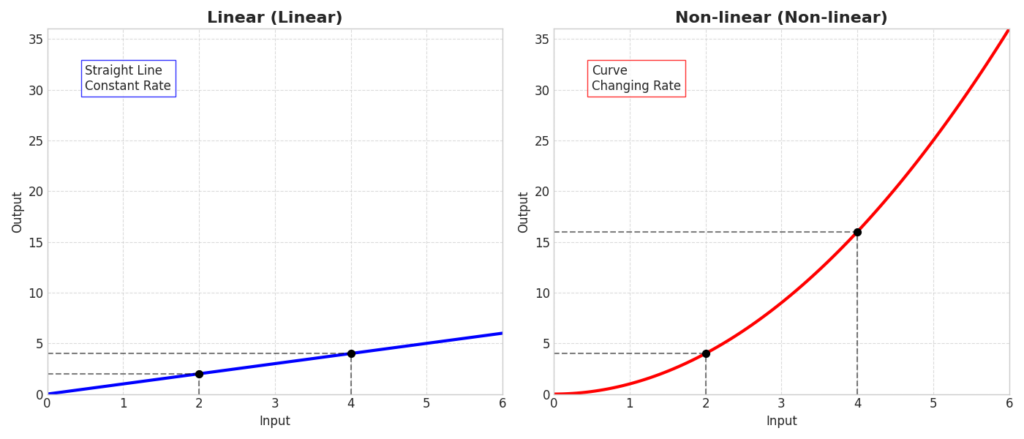
- 線形(Linear):グラフに書くと「直線」になるシンプルな関係です。原点を通る直線のような性質を持ち、入力が2倍になれば出力も2倍になる、といった素直な性質(線形性)があります。
- 非線形(Non-linear):グラフに書くと「曲線」になる複雑な関係です。世の中の現象の多くは、この非線形です。
AI(特にディープラーニング)が賢い理由は、この「非線形」の表現力が非常に高いからです。
直線(線形)だけで世界を区切ろうとしても限界がありますが、ぐにゃぐにゃと曲がる曲線(非線形)なら、猫と犬の画像を綺麗に分けられそうですよね。
グラフを見ても、曲線を描く関数は「曲がりくねり方」に特徴があることがわかります。
「極限」:限りなく近づくとどうなる?
次に、微分の基礎となる「極限(きょくげん)」についてお話しします。記号では (リミット)と書きます。
これは、「ある値に限りなく近づけたら、結果はどうなるか?」を想像することです。
「その値になる」のではなく、「近づく」というのがポイントです。
例えば、この関数を見てみましょう。
この をどんどん大きくしていったら(
)、値はどうなるでしょうか?
Pythonで実験してみましょう。
def complex_function(x):
return (2 * x) / (x**2 + 1)
# xをどんどん大きくしてみる
print("x=1のとき:", complex_function(1))
print("x=10のとき:", complex_function(10))
print("x=100のとき:", complex_function(100))
print("x=10000のとき:", complex_function(10000))結果を見ると、 が大きくなるにつれて、出力は
とどんどん
に近づいていくはずです。
つまり、「無限大の彼方ではゼロになるだろう」と予想できます。
これを数式で書くとこうなります。
グラフの端っこがどうなっているかを想像する力、それが極限です 。

なぜAIにこれが必要なのか?
「AIに関係あるの?」と思いましたか? 大ありです。
AIの学習とは、「誤差(間違い)」を可能な限り「ゼロ」に近づける作業だからです。
「誤差を最小にするには、パラメータをどの方向に動かせばいいか?」
これを考えるために、次回学ぶ「微分」が必要になり、微分の定義には、この「極限」の考え方が使われているのです。
つまり、極限は「AIが学習するためのコンパス」を作るための材料なのです。
今後の学習の指針
今回は、微分積分の入り口として、以下の2点を学びました。
- 関数は「入力を出力に変える装置」である。
- 極限は「変数をある値に近づけたときの、関数の行末を予想する」こと 。
次回は、いよいよ「微分」の計算に入ります。
微分とは、グラフの「接線の傾き」を求めること。
「傾き」がわかると、なぜAIが賢くなれるのか? その秘密を解き明かします。
【第2回】微分とは「変化の勢い」を知ること!AIが賢くなるための羅針盤
前回は、AIを「巨大な関数(入力と出力の変換装置)」として捉え、その行き着く先を予想する「極限」について学びました。
今回は、いよいよその関数を攻略するための最強の武器、「微分(びぶん)」についてお話しします。
「微分なんて、高校のテスト以来使っていないよ」
そんな方も多いと思います。しかし、AIにとっての微分は、テストで点を取るためのものではありません。「ゴール(正解)にたどり着くための羅針盤」なのです。
なぜ微分が羅針盤になるのか? 今日は数式よりも「イメージ」を大切にして解説していきます。
「少し動かすと、どう変わる?」を知りたい
まず、微分のことは一旦忘れて、こんな場面を想像してください。
あなたはエアコンのリモコンを持っています。部屋が少し暑いので、快適な温度にしたいと思っています。
でも、このリモコンのボタンには「温度を上げる」「下げる」という表示がなく、ただの「ダイヤル」がついているだけだとします。
ダイヤルを右に回すべきか、左に回すべきか、どうやって判断しますか?
とりあえず「少しだけ右に回してみる」のではないでしょうか。
- もし少し右に回して、涼しくなったら? → 正解!もっと右に回そう。
- もし少し右に回して、逆に暑くなったら? → 失敗!左に回すべきだ。
実は、これが「微分」の正体です。
「入力を変化させたら、出力はどれだけ変化するのだろうか?」
つまり、ある入力 を、ほんの少しだけ(
)変化させたとき、出力
がどれくらい変化するのか(
)。この変化の比率を求めることが微分です。
接線の傾き=変化の勢い
この「変化の比率」をグラフで見てみましょう。
曲がりくねった関数のグラフ上のある一点において、「もしそのまま真っ直ぐ進んだらどうなるか」を表す直線を引くことができます。これを「接線(せっせん)」と呼びます。
そして、微分の値は、この「接線の傾き」と同じ意味を持ちます。
- 傾きがプラス(右上がり): 入力を増やすと、出力も増える(勢いよく増加中)。
- 傾きがマイナス(右下がり): 入力を増やすと、出力は減る(減少中)。
- 傾きがゼロ(平ら): 増えも減りもしない。ここが「頂上」か「谷底」かもしれない!。
AIの学習において、私たちは「誤差(間違い)」という関数の「谷底(誤差が最小になる場所)」を探しています。
今いる場所の「傾き」さえわかれば、「どっちに進めば谷底に行けるか」がわかるのです。だから、微分は羅針盤なんですね。
数学的な定義と公式
イメージができたところで、少しだけ数式を見てみましょう。
前回学んだ「極限( )」が登場します。
変化の割合とは、「変化後の値 変化前の値」を「変化量」で割ったものでしたね。
この変化量( とします)を限りなく
に近づけたものが微分です。
これだけ覚えよう!魔法の公式
毎回この極限を計算するのは大変ですが、幸いなことに便利な公式があります。
AIの検定試験(E資格)で最もよく使うのが、次の「 の微分」です。
これだけ見ると呪文のようですが、ルールは簡単です。
「肩の数字を前に下ろして、肩の数字を1引く」。これだけです。
例を見てみましょう。
の場合:
肩の を前に出して、
乗にするので……
もし なら?
とても機械的な作業ですよね。これで、ある瞬間の「変化の勢い」が一瞬で計算できるようになったのです。
Pythonで「傾き」を計算してみよう
では、Pythonを使って、コンピュータに微分をさせてみましょう。
ここでは、公式を使わずに、微分の定義( をごく小さくする)に従って計算する「数値微分」をやってみます。
関数 の、
の地点での傾きを求めてみましょう。
手計算(公式)なら、 に
を代入して
になるはずです。
def my_function(x):
# 対象の関数: y = x^2
return x**2
def numerical_diff(f, x):
# 微小な値 h (0.0001)
h = 1e-4
# (f(x+h) - f(x)) / h
# ほんの少しずらして差を見る
return (f(x + h) - f(x)) / h
# x = 3 のときの傾きを求める
x_point = 3
slope = numerical_diff(my_function, x_point)
print(f"x={x_point} のときの傾き: {slope:.2f}")
実行結果は 6.00 (またはそれに極めて近い数字)になるはずです。
コンピュータは「公式」を知らなくても、こうして地道に少しずらした値を計算することで、傾き(微分)を求めているのです。

今後の学習の指針
今回は、微分の正体が「変化の比率(接線の傾き)」であることを学びました。
- 微分とは: 入力を少し変えたとき、出力がどう変わるかの勢い。
- なぜ必要か: 関数の谷底(正解)に向かう方向を知るため。
- 計算ルール:
は
になる。
さて、ここまでは「入力 がひとつだけ」の場合を考えてきました。
しかし、現実のAIは、何万、何億もの入力(パラメータ)を同時に扱います。
「変数がたくさんあるときは、どうやって微分するの?」
そこで登場するのが、次回解説する「偏微分(へんびぶん)」と、複数の関数を連携させる「連鎖律(れんさりつ)」です。
名前は難しそうですが、要は「ひとつずつ注目して微分する」というだけの話です。そしてこれこそが、ディープラーニングの学習アルゴリズム「誤差逆伝播法」の正体なのです。
【第3回】変数がたくさんあっても怖くない!「偏微分」と「連鎖律」
前回は、関数を「入力が出力に変わる装置」、微分を「その装置のレバーを少し動かしたときの変化の勢い(傾き)」として学びました。
しかし、前回の話にはひとつだけ「嘘」がありました。
それは、「入力(レバー)がひとつしかない」という前提で話していたことです。
実際のAI(ディープラーニング)の世界では、入力データや調整すべきパラメータ(重み)はひとつではありません。何万、何億個ものレバーが並んだ巨大なコクピットを想像してください。
「こんなにたくさんのレバーがあったら、どれを動かせばいいか分からないよ!」
そんなときに役立つのが、今回学ぶ「偏微分(へんびぶん)」と「連鎖律(れんさりつ)」です。
名前は厳めしいですが、考え方はとてもシンプル。「ひとつずつ考える」ことと「掛け合わせる」こと。たったこれだけです。
この2つこそが、現在のAIブームを支える学習アルゴリズム「誤差逆伝播法(バックプロパゲーション)」の正体なのです。
入力が複数あるときの「微分」=偏微分
AIのモデルでは、入力 がひとつだけでなく、
とたくさんあります。
例えば「家の価格」を予想するAIなら、「広さ」だけでなく「駅からの距離」「築年数」など、複数の入力がありますよね。
このように変数が複数ある関数のことを「多変数関数」と呼びます。
このとき、「広さを少し変えたら、価格はどう変わる?」を知りたいとします。でも、「駅からの距離」まで一緒に変わってしまったら、どっちの影響かわからなくなりますよね。
そこで、「注目している変数以外は、すべて定数(止まった数字)だと思い込む」ことにします。これが偏微分です。
記号が変わるだけ?
偏微分では、通常の微分の記号 の代わりに、独特な記号
(ラウンドディー、またはデル)を使います。
これは、「 や
は固定したまま、
だけを少し動かしたときの
の変化の割合」という意味です。
計算は驚くほど簡単
「他の変数は定数(普通の数字)だと思い込む」。これさえ守れば、計算は前回学んだ公式そのものです。
例えば、こんな関数があるとします。
で偏微分する(
):
は「定数(たとえば数字の5とか)」だと思い込みます。定数を微分すると
でしたね。だから、
の部分は消えてなくなります。残った
を微分して、答えは
です。
で偏微分する(
):今度は
を「定数」だと思い込みます。
はただの数字なので、微分すると消えます。残った
(
)を
で微分すると、係数だけが残るので、答えは
です。
このように、偏微分とは「ターゲット以外を無視する」という都合のいい計算方法なのです。
関数のリレーをつなぐ「連鎖律」
次に紹介するのは「連鎖律(チェーンルール)」です。
AI、特に「ディープラーニング(深層学習)」は、関数の中にさらに関数が入っているような「多層構造」をしています。
入力 が関数
で
になり、その
がさらに関数
で
になる……というようなリレー形式です。
このとき、「大元の を動かしたら、最後の
はどれくらい動くの?」を知りたくなりますよね。
これを求める魔法のルールが連鎖律です。
掛け算でつながる
結論から言うと、それぞれのステップでの「微分の掛け算」で求められます。
:
が変わると
がどれくらい変わるか
:
が変わると
がどれくらい変わるか
この2つを掛け合わせれば、 から
への影響力がわかるのです。まるで分数の約分のように、間の
が消えるように見えるのが面白いですよね。
これがAIの学習において、出口(出力層)の誤差の原因を、入り口(入力層)に向かって遡って特定していく「誤差逆伝播法」の数学的な裏付けになっています。
Pythonで「偏微分」を体験しよう
それでは、Pythonを使って偏微分の計算(数値微分)を行ってみましょう。
今回は、2つの変数 を持つ関数について、それぞれの偏微分係数を計算します。
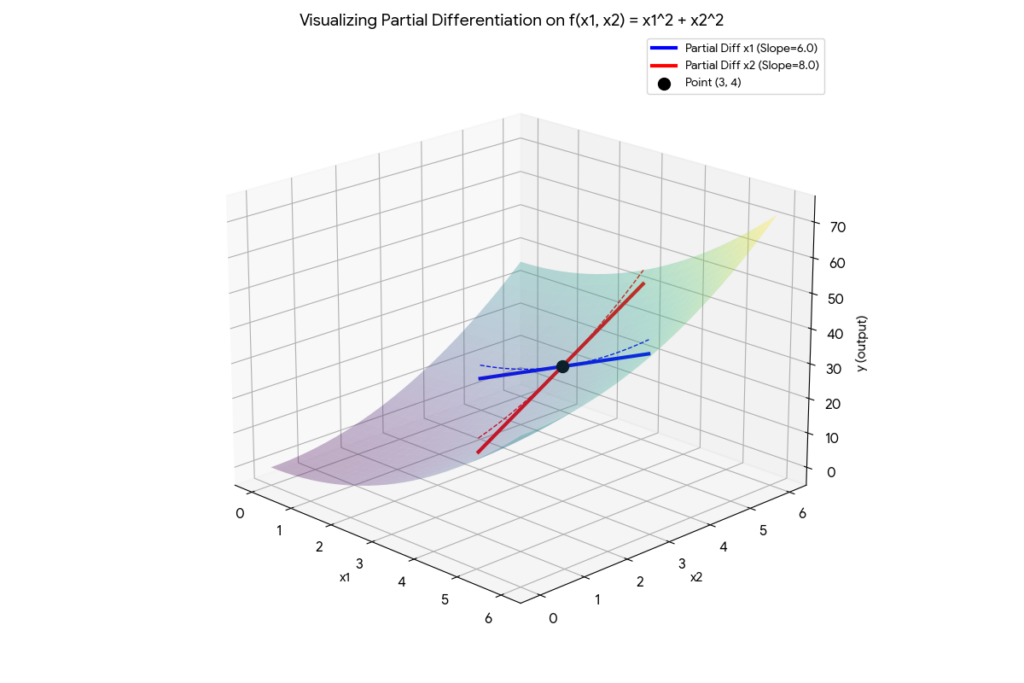
対象の関数:
(お椀のような形をしたグラフになります)
import numpy as np
def my_multivariable_function(x1, x2):
# y = x1^2 + x2^2
return x1**2 + x2**2
def numerical_partial_diff(f, x1, x2, target_var):
h = 1e-4
if target_var == 'x1':
# x1 だけを少し(h)動かす。x2 はそのまま。
return (f(x1 + h, x2) - f(x1, x2)) / h
elif target_var == 'x2':
# x2 だけを少し(h)動かす。x1 はそのまま。
return (f(x1, x2 + h) - f(x1, x2)) / h
# 計算する場所
x1_val = 3.0
x2_val = 4.0
# x1 での偏微分(理論値は 2*x1 = 6.0)
grad_x1 = numerical_partial_diff(my_multivariable_function, x1_val, x2_val, 'x1')
print(f"x1についての偏微分 (x1={x1_val}): {grad_x1:.2f}")
# x2 での偏微分(理論値は 2*x2 = 8.0)
grad_x2 = numerical_partial_diff(my_multivariable_function, x1_val, x2_val, 'x2')
print(f"x2についての偏微分 (x2={x2_val}): {grad_x2:.2f}")
コードを見ると、「微分したい変数にだけ を足して、他はそのままにしている」ことがわかりますね。これが偏微分のプログラム的な実装です。
今後の学習の指針
今回は、AIの学習を理解するための最重要ツールである2つの概念を学びました。
- 偏微分: 変数がたくさんあっても、ひとつに注目して他を固定すれば単純な微分と同じ。
- 連鎖律: 関数が重なっていても、それぞれの微分を掛け算すれば全体の影響力がわかる。
「ひとつずつ解く」「掛け合わせる」。
複雑に見えるニューラルネットワークも、実はこの単純なルールの積み重ねで動いているのです。
さて、微分(分解すること)ばかりやってきましたが、数学にはもうひとつ大きな柱がありますね。そう、「積分(せきぶん)」です。
「微分は傾きだけど、積分って何? AIに関係あるの?」
次回は、積分のイメージ(面積を求めること)と、それが確率や統計においてどう使われるのかについて解説します。微分とは逆の「積み上げる」プロセスを楽しみにしていてください。
【第4回】微分の逆?「積分」で面積を求める意味とは
前回までは、関数の傾き(変化の勢い)を求める「微分」について学んできました。
今回は、その逆の操作にあたる「積分(せきぶん)」についてお話しします。
「微分は傾き、じゃあ積分は何?」
一言で言えば、積分とは「面積」を求めることです。
そして、AIの学習において積分は、確率の計算や、データの合計値を扱う場面で非常に重要な役割を果たします。
微分ほど頻繁に主役になるわけではありませんが、統計学や機械学習の理論を支える縁の下の力持ちです。
今回は、積分のイメージと、それがなぜ「微分の逆」と呼ばれるのか、そしてPythonでの計算方法について解説します。
積分とは「微小な足し算」である
まず、「積分」という漢字を見てみましょう。「分」けて「積」む、と書きますね。
これは、対象を細かく分解して、それを積み上げて(足し合わせて)いくという意味です。
積分とは「微小なものを足し合わせる演算」です。
インテグラル記号の正体
積分の記号といえば、細長いSのようなマーク です。これを「インテグラル」と読みます。
実はこの記号、英語で「合計」を意味する Summation(サメーション) の頭文字「S」を縦に引き伸ばしたデザインなんです。
数式で と書いたとき、これは次のようなメッセージになります。
「関数 の高さを持つ、横幅がごくわずかな(
)短冊を、全部足し合わせなさい(Sumしなさい)」
無数の細い短冊を並べて足し合わせると、結果的にそれはグラフの下側の「面積」になりますよね。これが積分の正体です。
なぜ「微分の逆」なのか?
学校では「微分と積分は逆の関係」と習いますが、これはどういうことでしょうか。
微分は「ある瞬間の変化の勢い( と
の比率)」を求めるものでした。
逆に積分は、その「変化の勢い」と「変化した量」を足し合わせて、元の関数の姿を復元する作業だと言えます。
例えば、車のスピードメーター(速度)をずっと記録していたとします。
「速度」は「距離」を微分したものです(距離の変化の勢いだから)。
逆に、記録された「速度」を時間の経過に沿って足し合わせていけば(積分すれば)、実際に走った「距離」がわかりますよね。
謎の定数「C」の正体
ただし、積分にはひとつだけ弱点があります。
それは「スタート地点(初期値)がわからないと、完全には元に戻せない」ということです。
例えば、「時速100kmで1時間走った」という情報だけあっても、「東京から出発したのか」「大阪から出発したのか」まではわかりません。移動距離はわかりますが、現在の場所を特定するには「出発地点」の情報が必要です。
この「不明なスタート地点」のことを、数学では積分定数(せきぶんていすう)と呼び、通常 という記号で表します。
式で書くとこうなります。
「微分して になる関数は
だけど、
かもしれないし、
かもしれないから、とりあえず
と書いておこう」
ということです。これを不定積分(ふていせきぶん)と呼びます。
一方で、「0秒から10秒の間」のように区間を決めて面積を求める場合、この は打ち消しあって消えるため、確定した値(面積)が出ます。これを定積分(ていせきぶん)と呼びます。
AIにおける積分の役割
AIエンジニアにとって、積分が特に重要になるのは「確率・統計」の分野です。
例えば、あるデータがどのような分布をしているかを表す「確率密度関数(かくりつみつどかんすう)」というものがあります。
この関数のグラフの下側の面積は、確率そのものを表します。
「全区間で積分すると(面積を求めると)、確率は必ず (100%)になる」という性質は、AIの理論で頻繁に使われます。
また、連続的に変化するデータの「期待値(平均のようなもの)」を計算する際にも、シグマ( )を使った単なる足し算ではなく、積分(
)を使った計算が必要になります。
Pythonで「面積」を求めてみよう
では、Pythonを使って積分(定積分)を行い、面積を求めてみましょう。
科学技術計算ライブラリ SciPy (サイパイ)の integrate モジュールを使えば、複雑な計算も一行です。
ここでは、関数 の、
が
から
までの範囲の面積を求めてみます。
手計算だと、 を積分して
になり、
を代入すると
になるはずです。
from scipy import integrate
def my_function(x):
# 対象の関数: y = x^2
return x**2
# 積分を実行 (0から1まで)
# quad関数は (積分値, 推定誤差) の2つを返します
area, error = integrate.quad(my_function, 0, 1)
print(f"計算された面積: {area}")
print(f"推定誤差: {error}")
実行結果を見ると、 0.3333... という値が得られるはずです。
コンピュータ内部では、非常に細かく区切った台形や長方形の面積を高速に足し合わせることで、この値を算出しています(区分求積法のようなイメージです)。

今後の学習の指針
今回は、微分の逆操作である「積分」について学びました。
- 積分とは:微小な変化を足し合わせて、面積や元の量を求めること。
- 不定積分:元の関数を推測するが、定数
(初期値)が決まらない。
- 定積分:範囲を決めて面積を確定させる。確率の計算などで重要。
これで、AIに必要な「関数」「微分」「積分」の3大要素が揃いました。
次回は、いよいよこれらを組み合わせて、AIが自動で学習する(賢くなる)ための具体的な仕組み、「最適化(さいてきか)」と「勾配降下法(こうばいこうかほう)」について解説します。
「微分を使って、関数の谷底へ降りていく」。
その冒険の様子を、数式とPythonで体験しましょう。
【最終回】AIが「学習」する瞬間!勾配降下法と最適化の魔法
微分積分の旅、これまで「関数」「微分」「積分」と基礎固めをしてきましたが、いよいよ今回が最終回です。
「で、結局これらの数学がどうやってAIを賢くするの?」
その答えが、今日お話しする「最適化(さいてきか)」と「勾配降下法(こうばいこうかほう)」です。
これは、AIが自動で試行錯誤を繰り返し、正解にたどり着くためのアルゴリズムそのものです。
微分が「羅針盤」だと言った意味が、ここで完全に明らかになります。
それでは、AIが「学習」する瞬間のメカニズムを、一緒に見ていきましょう。
AIのゴールは「誤差」をゼロにすること
まず、AIにとっての「学習」とは何をすることなのか、再確認しましょう。
AI(ニューラルネットワーク)は、内部にたくさんの「重み(パラメータ)」を持った巨大な関数でしたね。
学習とは、この重みを調整して、望み通りの出力を出す関数を作ることです。
では、「望み通り」かどうかをどうやって判断するのでしょうか?
ここで登場するのが「誤差関数(ごさかんすう)」(損失関数とも呼ばれます)です。
- AIの出力した答え:
- 本当の正解データ:
この2つのズレ(距離)を計算します。
よく使われるのは、ズレを2乗して合計する「二乗誤差」です。
この誤差 が大きければ「全然ダメ」、小さければ「賢い」ということになります。
つまり、AIの学習のゴールは、この誤差関数 の値が一番小さくなる(ゼロに近づく)ような重み
を見つけることなのです。これを「最適化」と呼びます。
山降りのアルゴリズム「勾配降下法」
誤差関数 を、横軸に重み
、縦軸に誤差の大きさ
をとってグラフにすると、谷のような形になります。
私たちは、この谷の「一番底(誤差が最小の地点)」に行きたいわけです。
しかし、AIのパラメータは何万個もあり、グラフは複雑に入り組んでいます。いきなり「ここが底だ!」と計算するのは不可能です。
そこで、「勾配降下法(Gradient Descent)」という方法を使います。
これは、濃い霧の中で山を降りるようなものです。
周りの景色(全体の形)は見えませんが、足元の「傾斜」だけはわかります。
- 今いる場所の「傾き(勾配)」を調べる(微分する)。
- 傾きが下っている方向へ、ほんの「一歩」だけ進む。
- 移動した先で、また傾きを調べる。
- これを繰り返せば、いつかは谷底に着くはず!
これがAI学習の基本原理です。
学習の方程式:重みの更新ルール
この「山降り」を数式にすると、非常にシンプルです。
AI学習の最重要公式がこちらです。
記号の意味を解説します。
(重み): AIの調整ダイヤル。
(勾配): 誤差関数の傾き。微分で求めます。
(イプシロン):「学習率」と呼ばれるパラメータ。一歩の歩幅の大きさです。
- マイナス(-): これが重要です。「傾きと逆方向」に進むことを意味します。
考えてみてください。
傾きがプラス(右上がり)なら、谷底に行くには「左(マイナス方向)」に戻らないといけませんよね。
逆に、傾きがマイナス(右下がり)なら、谷底は「右(プラス方向)」にあります。
だから、傾きの値を引くことで、自動的に谷底に向かう方向に修正されるのです。
この更新を何千回、何万回と繰り返すことで、AIは徐々に「誤差の少ない」賢いモデルへと進化していきます。
Pythonで「山降り」を体験しよう
それでは、Pythonで勾配降下法を実装してみましょう。
シンプルな二次関数 の最小値(谷底)を探してみます。
(計算すれば で最小になることはわかりますが、あえて微分を使って探させます)
import numpy as np
# 1. 対象の関数 (誤差関数のイメージ)
# y = x^2 - 4x + 6
def error_function(x):
return x**2 - 4 * x + 6
# 2. 導関数 (傾きを求める関数)
# y' = 2x - 4
def derivative(x):
return 2 * x - 4
# --- 勾配降下法の実行 ---
# 初期位置 (適当な場所からスタート)
current_x = -5.0
# 学習率 (一歩の大きさ)
learning_rate = 0.1
# 繰り返す回数
epochs = 20
print(f"スタート地点: x = {current_x}")
for i in range(epochs):
# 今いる場所の傾きを計算
grad = derivative(current_x)
# 重みの更新: x <- x - 学習率 * 傾き
current_x = current_x - learning_rate * grad
# 経過を表示
loss = error_function(current_x)
print(f"回数: {i+1}, x: {current_x:.4f}, 誤差(y): {loss:.4f}")
print("-" * 30)
print(f"最終結果: x = {current_x:.4f}")
print("正解 (x=2.0) に近づけましたか?")実行すると、最初は正解から遠かった が、回数を重ねるごとにどんどん
に近づいていく様子が見えるはずです。
これが、コンピュータの中で行われている「学習」の正体です。

シリーズまとめ:AIエンジニアへの第一歩
全5回にわたる「ゼロから学ぶ微分積分」、いかがでしたでしょうか。
- 関数と極限: AIは入力を出力に変える巨大な装置。
- 微分: 「変化の勢い(傾き)」を知るためのツール。
- 偏微分と連鎖律: 複雑なAIモデルを解きほぐすための鍵。
- 積分: 面積や確率を扱うための基礎。
- 勾配降下法: 微分を使って、自動的に正解(谷底)を探す学習アルゴリズム。
これらの数学知識は、E資格の試験だけでなく、AIの論文を読んだり、新しいモデルを実装したりする際の強力な武器になります。
「数式は、AIという魔法を記述するための言語」です。
最初は難しく感じるかもしれませんが、コードと照らし合わせながら少しずつ慣れていけば大丈夫です。
この連載が、皆さんのAIエンジニアとしての第一歩になれば幸いです。
最後までお読みいただき、本当にありがとうございました!