カイ二乗検定とは
カイ二乗検定とは何か?
カイ二乗検定(かいにじょうけんてい、Chi-square test)は、データの中にある観測結果と予測結果がどれくらい一致しているかを確認するための統計的手法です。主に、カテゴリーデータ(分類データ)の分析に用いられます。簡単に言えば、観測されたデータが「偶然の産物」か、それとも「何かしらの影響があるのか」を判断するために使われる検定です。
例えで理解するカイ二乗検定
例えば、サイコロを6回振ったときに、それぞれの目が1回ずつ出ることを期待するとします。しかし、実際に振ってみると、特定の目が多く出たり少なく出たりするかもしれません。この場合、サイコロが「公平かどうか」を判断するためにカイ二乗検定を使います。もし、サイコロが公平であれば、すべての目がほぼ同じ回数出るはずです。カイ二乗検定を使うと、観測された結果が偶然によるものか、それともサイコロが偏っているのかを判断できます。
カイ二乗検定の種類
カイ二乗検定には主に2つの種類があります。
1. 適合度検定
適合度検定は、観測されたデータが理論的な期待値(予想される分布)とどれだけ一致しているかを調べる検定です。例えば、理論上は50%の確率で成功するイベントがあると仮定し、実際に試行してみた結果がその期待に合致しているかを検証します。
例:
あるテストで100人の学生がA、B、C、Dの4つの成績に分かれるとします。成績の分布が均等(各成績25人ずつ)だと期待される場合、実際の分布がこの期待にどれだけ合っているかをカイ二乗適合度検定で確かめます。
2. 独立性の検定
独立性の検定は、2つのカテゴリ変数が互いに関連しているかどうかを調べる検定です。たとえば、性別と趣味が関連しているかどうかを検証する場合などに使われます。
例:
ある学校で、男子と女子の間で好きなスポーツが異なるかどうかを調べたいとします。この場合、カイ二乗独立性の検定を使って、性別と好きなスポーツに関連性があるかを検証します。
前提条件
カイ二乗検定を適切に行うためには、いくつかの前提条件があります。以下にその主な前提条件を挙げます。
1. 独立性
- 各観測データが互いに独立していることが前提です。つまり、あるカテゴリの観測結果が他のカテゴリの結果に影響を与えないことが必要です。
2. 期待頻度の大きさ
- 各セル(クロス集計表の各カテゴリの組み合わせ)における期待頻度が十分に大きいことが前提です。具体的には、各セルの期待頻度が5以上であることが望ましいとされています。期待頻度が小さい場合、カイ二乗検定の結果が不正確になる可能性があり、その場合はフィッシャーの正確確率検定などの代替手法が検討されます。
3. データのカテゴリカル性
- カイ二乗検定はカテゴリカルデータ(名義尺度または順序尺度)を扱います。従って、分析対象のデータがカテゴリカルデータであることが前提です。
4. サンプルサイズ
- サンプルサイズが大きいことが望ましいです。カイ二乗検定はサンプルサイズが小さい場合に結果が安定しないことがあります。サンプルサイズが十分に大きいことで、期待頻度が5以上になることが保証されやすくなります。
5. 観測データの総計の固定
- カイ二乗検定では、観測データの総計が固定されていることが前提です。これにより、各カテゴリの観測頻度が互いに独立したデータとみなされ、検定が適切に行われます。
カイ二乗検定の計算方法
カイ二乗検定の基本的な計算の流れを説明します。
1. 観測データと期待値を用意する
観測データとは、実際に得られたデータのことです。一方、期待値とは、理論上期待されるデータのことです。
例:
先ほどの成績の例で考えると、観測データが {A: 20人, B: 30人, C: 25人, D: 25人} であり、期待値が {A: 25人, B: 25人, C: 25人, D: 25人} だとします。
2. カイ二乗値を計算する
カイ二乗値は次の式で計算されます。

この計算を各カテゴリについて行い、すべてを合計した値がカイ二乗値です。
例:
各成績のカイ二乗値を計算してみます。
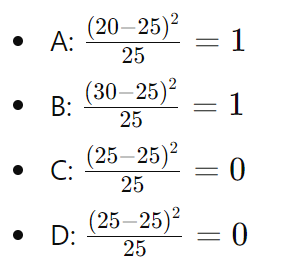
これらを合計すると、カイ二乗値は 1 + 1 + 0 + 0 = 2 となります。
3. 自由度とカイ二乗分布表を使って判断する
カイ二乗値が大きいほど、観測データと期待値が大きく異なっていることを意味します。次に、カイ二乗分布表を使って、この値が統計的に有意かどうかを判断します。ここで、「自由度」という概念が必要になります。自由度とは、データの独立した要素の数に基づいて決まる値です。
カイ二乗検定の自由度(degrees of freedom, df)の求め方は、使用するカイ二乗検定の種類によって異なりますが、ここでは代表的な2つのケースについて説明します。
1. 適合度検定(Goodness-of-Fit Test)
適合度検定は、観察データが特定の理論分布にどれだけ適合しているかを確認するために使用されます。この場合、**自由度は「カテゴリの数 - 1」**で求められます。
自由度の計算式
自由度=k−1
ここで、kはカテゴリの数です。
例
例えば、サイコロを6回振って得られた目の出現回数が、均等(すべての目が出る確率が同じ)であるかどうかを検定する場合、カテゴリ数は6です。この場合の自由度は次のようになります:自由度= 6 - 1 = 5
2. 独立性の検定(Test of Independence)
独立性の検定は、2つのカテゴリ変数が互いに独立しているかどうかを確認するために使用されます。この場合、**自由度は「(行の数 - 1)×(列の数 - 1)」**で求められます。
自由度の計算式
自由度=(r−1)×(c−1)
ここで、rは行の数、cは列の数です。
例
例えば、性別(男性・女性の2種類)と、趣味(スポーツ、読書、映画の3種類)の関連性を検定する場合、行の数は2、列の数は3です。この場合の自由度は次のようになります:
自由度=(2−1)×(3−1)==1×2=2
自由度の解釈
自由度は、データがどれだけの「独立した情報」を持っているか、または制約を受けていないかを表す指標です。カイ二乗検定では、自由度に応じてカイ二乗分布表から臨界値を参照し、観測データが期待値からどれだけずれているかを判断します。
これらの計算式を正確に理解し、状況に応じて適用することがカイ二乗検定を正しく使うためには重要です。
カイ二乗分布のグラフ
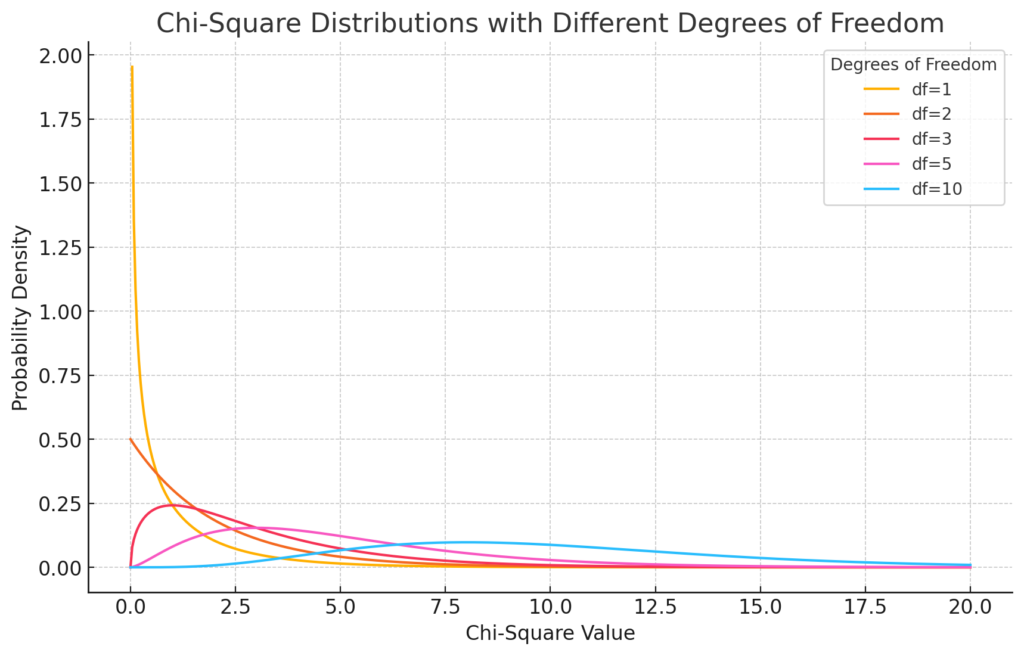
自由度を変化させたときのカイ二乗分布のグラフです。自由度が増えるにつれて、分布の形状が変化していることがわかります。
自由度が1のとき、分布は大きく右に偏り、ピークが低くなっています。
自由度が増えると、分布は徐々に右にシフトし、ピークが低く、広がりが増していきます。
自由度が大きくなるにつれて、分布はより対称に近づき、平均値も高くなります。
このように、カイ二乗分布は自由度によってその形状が大きく異なり、自由度が高くなるほど、分布が広がり、より正規分布に近い形状になります。
カイ二乗検定の意義
カイ二乗検定は、データが偶然の産物か、それとも何かしらの影響があるかを判断する強力なツールです。特に、マーケティング調査や社会科学の研究などで、カテゴリデータを分析する際に頻繁に用いられます。
今後の学習の指針
カイ二乗検定を理解したら、実際に手元のデータを使って計算してみると理解が深まります。また、他の統計検定(例えば、t検定やANOVA)との違いを学ぶことで、より多様なデータ分析手法に精通することができます。特に、Excelや統計ソフトを使ってカイ二乗検定を実行する方法を学ぶと、実務での活用がより効果的になるでしょう。
投稿者プロフィール

- 代表取締役
-
セイ・コンサルティング・グループ株式会社代表取締役。
岐阜県出身。
2000年創業、2004年会社設立。
IT企業向け人材育成研修歴業界歴20年以上。
すべての無駄を省いた費用対効果の高い「筋肉質」な研修を提供します!
この記事に間違い等ありましたらぜひお知らせください。
学生時代は趣味と実益を兼ねてリゾートバイトにいそしむ。長野県白馬村に始まり、志賀高原でのスキーインストラクター、沖縄石垣島、北海道トマム。高じてオーストラリアのゴールドコーストでツアーガイドなど。現在は野菜作りにはまっている。

