変動係数とは？

変動係数（へんどうけいすう、Coefficient of Variation、略してCV）について説明します。初めて聞く言葉かもしれませんが、統計やデータ分析を行う際に非常に役立つ指標です。

変動係数とは？

変動係数は、データのばらつきを評価するための指標です。具体的には、データの標準偏差をその平均値で割った値で表されます。式で書くと、次のようになります。

この式を見るとわかるように、変動係数は「標準偏差」と「平均」の比率を示しています。これにより、データのばらつき具合を相対的に評価することができるのです。たとえば、データがどれだけ広がっているかを平均値に対して測ることができます。

なぜ変動係数を使うのか？

他の統計指標である「標準偏差」や「分散」もデータのばらつきを示しますが、これらは単位に依存するため、異なる単位のデータを比較する際には使いにくいことがあります。一方、変動係数は無次元量、つまり単位を持たないため、異なる単位や異なるスケールのデータ同士を比較する際に非常に便利です。

例えば、ある製品の品質管理を考えてみましょう。製品Aの平均重量が100gで、標準偏差が5g、製品Bの平均重量が200gで、標準偏差が10gだとします。この場合、両者の標準偏差は異なりますが、変動係数を計算するとどちらも5%となり、品質のばらつきは同じ程度だと判断できます。

変動係数の計算例

実際に変動係数を計算してみましょう。

あるクラスのテストの結果が次のようなものであったとします。

• 平均点：80点
• 標準偏差：10点

このときの変動係数は次のように計算できます。

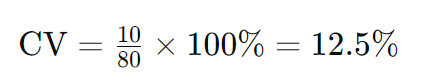
この結果は、テストの点数のばらつきが平均点に対して12.5%であることを示しています。

変動係数のメリットとデメリット

メリット

• 異なる単位やスケールのデータを比較できる
• データのばらつきを直感的に理解しやすい

デメリット

• 平均が0に近いと変動係数が大きくなるため、解釈が難しくなる
• 平均が負の値になるときに、標準偏差との比率が直感的でなくなる

偏差値との違い

偏差値とは？

一方、偏差値はあるデータが集団の中でどの位置にあるかを示す指標です。平均を50、標準偏差を10としたとき、そのデータが平均からどれだけ離れているかを示します。学校のテストなどで使われることが多く、全体の中で自分の得点がどの程度の位置にあるのかを簡単に理解できるようにします。

偏差値を使うべき場面

• 個人の成績や位置を評価するとき: 学校の成績や試験の結果など、個々のデータが集団内でどの位置にあるかを知りたい場合に使います。
• データの標準化を行うとき: 異なるテストの結果を比較する際に、偏差値を使うことで、異なるテストでも同じ基準で評価できます。

どちらを使うべきか？

変動係数を使うべき状況

• 異なるスケールや単位のデータを比較する必要があるとき
• データのばらつきを相対的に評価したいとき
• 集団全体のばらつき具合を比較する場合

偏差値を使うべき状況

• 個人の成績やデータが、集団内でどの位置にあるかを知りたいとき
• 異なる試験や評価基準を統一的に比較したいとき
• 学校の成績やテストの結果を他の学生と比較する場合

例えで理解しよう

例えば、あるクラスでのテスト結果を考えてみましょう。もし、クラスの成績がどれだけばらついているかを見たいなら、変動係数が適しています。一方、個々の生徒がクラスの中でどの位置にいるか、つまり自分の得点がクラス内でどれだけ高いかを知りたいなら、偏差値を使うのが適しています。

まとめ

変動係数はデータのばらつきを相対的に評価するための便利な指標です。特に、異なる単位やスケールのデータを比較する際に非常に役立ちます。ただし、平均値が0に近い場合や負の値を取る場合には、慎重に解釈する必要があります。

今後、データ分析や統計の勉強を進める際には、この変動係数を使ったデータの比較方法を意識してみてください。様々な場面で役立つことがわかるでしょう。