ビジネスデータ分析の基礎

この記事では、ビジネスに活用するデータ分析ということで確率・統計を解説しています。Excelを使った操作も解説の予定です。

正解

1．データ分析と確率・統計

（１）ビジネスデータ分析の目的

正解

正解: 2. パフォーマンスの評価と最適化

ビジネスデータ分析は、組織がより効果的に意思決定を行い、競争力を高めるために不可欠なプロセスです。この分析は、過去のパフォーマンスを理解し、未来のトレンドを予測し、ビジネス戦略を最適化するのに役立ちます。ビジネスデータ分析の主な目的は以下の5点です。

パフォーマンスの評価と最適化

ビジネスデータ分析の最も基本的な目的は、企業のパフォーマンスを評価し、プロセス、製品、またはサービスを最適化する方法を特定することです。データを活用して、売上高、顧客満足度、オペレーションの効率性など、様々なパフォーマンス指標を分析し、改善の余地を見つけ出します。

意思決定のサポート

データ駆動型の意思決定は、直感や経験だけに頼るよりも、はるかに効果的です。データ分析を通じて、経営陣はリスクを評価し、機会を特定し、戦略的な決定を下すための客観的な根拠を得ることができます。これにより、リソースの配分、マーケティング戦略、製品開発などの分野でより良い決定が可能になります。

トレンドとパターンの特定

市場や顧客の行動におけるトレンドとパターンを特定することは、ビジネスが競合他社の一歩先を行くのに役立ちます。データ分析を用いて、需要の変動、顧客の好みの変化、新しい市場機会などを予測し、それに応じた戦略を立てることができます。

リスク管理と予測

ビジネスは不確実性と常に隣り合わせです。データ分析により、潜在的なリスクを予測し、その影響を最小限に抑えるための戦略を立てることが可能になります。これには、金融リスク、サプライチェーンの中断、市場の変動などが含まれます。

顧客理解の深化

最終的に、ビジネスデータ分析は、企業が顧客をより深く理解し、彼らのニーズに応える製品やサービスを提供するのに役立ちます。データを分析することで、顧客の購買行動、好み、フィードバックなどを詳細に把握し、顧客満足度を高めることができます。

ビジネスデータ分析は、これらの目的を達成するための強力なツールであり、組織がデータを戦略的な資産として利用することを可能にします。効果的なデータ分析プロセスにより企業はパフォーマンスを向上させ、競争優位性を獲得し、持続可能な成長を達成することができるでしょう。

（２）なぜ、確率・統計は必要なのか？

日常業務におけるデータ集計作業は、表面的には簡単なタスクに見えるかもしれませんが、その背後には、データから実際に意味ある洞察を引き出すという、非常に重要なプロセスが存在します。例えば、顧客の購買データの分析や、月間のウェブサイト訪問者数の集計など、単純な数字の足し算や平均の算出を超えた深い分析が求められます。これらの分析作業は、多くの場合、専門的な統計的知識を必要とせず、基本的な数値処理が中心となりがちです。

たとえば、特定の商品に関する顧客フィードバックを200件収集し、顧客満足度を把握することを考えます。「非常に満足」と回答した顧客の数を単純にカウントすることで、その商品の満足度が計算できます。もし160人が「非常に満足」と答えた場合、満足度は80%となります。同じく、あるカフェのコーヒー販売データを分析したところ、1日平均で販売されるコーヒーの数が70杯であることが判明しました。ピーク時には120杯を販売し、閑散期には最低でも30杯は売れる日もあることから、これらの数字は過去のビジネスパフォーマンスを把握するための基本的なデータ集計の例です。

しかし、これらのシンプルなケースを超えて、より複雑な統計的分析が必要な状況もあります。先に挙げた商品の顧客フィードバックの例で、昨年は200件のフィードバックのうち160件が「非常に満足」という結果だったとします。今年、その数が170件に増加した場合、実際に商品の満足度が向上したと言えるのか、あるいはこの10件の増加は単なる統計上の偶然なのかを検証する必要があります。また、カフェのコーヒー販売データについても、1日平均70杯の販売に基づいて翌日の準備量を計画するのは合理的ですが、それが本当に最適な判断なのかを確かめるためには、需要の変動や予測ミスによる損失を最小化するためのより高度な統計モデルの適用が求められます。

統計は、数字を単に集めてカウントする以上の価値を提供します。それは、集められたデータに深みを与え、そのデータが何を示しているのかを解釈し、将来の予測を立てる能力を備えています。従来のデータ分析作業が数字の集計に焦点を当てていたのに対し、統計学はその数値が示す背景や動向を読み解き、より戦略的な意思決定を支援します。

このように統計学は、ビジネスのあらゆる面で重要な役割を担っており、単なる数値集計を超えた価値を企業にもたらすのです。

（３）データ分析の手法

データ分析はビジネスや研究において重要な役割を果たしています。主に「現状の把握」と「未来の検証や予測」の二つの大きな機能に分類できます。これらの機能にはさまざまな手法があり、それぞれの目的に応じて使い分けられます。以下で、これらの機能と手法について詳しく解説します。

現状把握のためのデータ分析

現状を把握するためには、まずデータの集計が必要になります。これには主に二種類のデータが関わります。一つ目は数値を扱う量的データの集計で、例えば売上高や顧客訪問回数などの数値データを指します。もう一つは質的データ（カテゴリーデータ）の集計で、顧客の属性（年齢層や性別）、商品の種類、アンケートの選択肢（満足・不満足など）といったものがこれにあたります。これらの集計方法は記述統計と呼ばれ、データの特徴を要約し、現状を明確にするために用いられます。

未来の検証や予測

検証や予測を行うためのデータ分析では、推測統計が中心となります。

推測統計（すいそくとうけい）は、データをもとにして「全体の様子」を推測する方法です。

簡単なイメージ

1. クラス全員の身長：例えば、あなたのクラスの全員の身長を知りたいとします。でも、クラス全員に身長を聞くのは大変なので、何人かだけに聞いて、その結果からクラス全員の身長を推測します。
2. サンプルを取る：クラスの中からランダムに10人を選んで、その人たちの身長を測ります。この10人のデータを「サンプル」と呼びます。
3. サンプルの平均：10人の身長の平均を計算します。この平均が、クラス全員の身長の平均に近いと考えます。

推測統計のポイント

• ランダムサンプル：選ぶ人がランダムであればあるほど、そのサンプルが全体をよく表していると考えられます。
• サンプルサイズ：サンプルの人数が多ければ多いほど、推測が正確になります。
• 信頼区間：サンプルから得られた平均値だけでなく、その周りの範囲（たとえば「この範囲にクラス全体の平均があるはず」という範囲）も考えます。

具体的な例

例えば、クラスの全員が30人いて、その中から10人の身長を測ったとします。その10人の平均身長が160cmだったら、「クラス全員の平均身長もだいたい160cmぐらいだろう」と推測します。

まとめ

推測統計は、少ないデータから全体の特徴を推測するための方法です。たくさんのデータを集めるのが難しいときに、少ないデータでも全体の様子を知ることができる便利な方法です。

簡単に言うと、「一部の情報から全体を予測する」ための技術が推測統計です。例えば、クラスの10人の身長を測るだけで、クラス全体の平均身長を予測することができるのです。

推測統計の分野では主に三つの手法があります。

1. 検定

異なる集団間で収集したデータに基づいて、例えば新商品と既存商品の売上高を比較し、その平均値に統計的に有意な差が存在するかを検証します。この手法は、単に平均値や比率に差があることを示すだけでなく、その差が偶然によるものではないことを確かめるために用いられます。検定は、マーケティングキャンペーンの効果分析や顧客満足度調査など、多岐にわたる領域で活用されています。

2. 相関分析

相関分析は、二つの変数間の関係を探る手法です。例えば、広告投資額と売上高の関係や、顧客満足度と再購入率との間にどのような関連があるかを調べます。この分析を通じて、ビジネス上の重要な因果関係や相関関係を発見することができます。

3. 多変量解析

多変量解析は、より複雑なデータ関係を解析するために用いられる手法群です。これには、消費者の購買行動を予測する回帰分析、顧客を似た特徴ごとにグループ分けするクラスター分析、重要な変数を抽出するための因子分析、データから決定ルールを導き出す決定木などがあります。これらの手法は、顧客セグメンテーション、リスク管理、商品開発など、様々なビジネスプロセスの最適化に貢献しています。

データ分析のこれらの手法は、単に現状を把握するだけでなく、将来のビジネス戦略を立てる上での重要な基盤を提供します。統計学の原理と解析技術を駆使することで、より効率的かつ効果的な意思決定が可能になり、ビジネスの成長を加速させることができます。

（４）データ分析の流れ

データ分析のプロセスは、

• データの収集と整理
• データの集約と分析
• 分析結果の解釈と意思決定

というステップを踏むことになります。この流れを適切に管理することで、ビジネスにおける意思決定の精度を高めることができます。しかし、単に利用可能なデータがあるからといって分析を実施しても、有益な洞察や結果を得られるとは限りません。目的に基づいて、分析に必要なデータを慎重に選定し収集することが、成功への鍵を握ります。アウトプットの質は、使用するデータの質に大きく依存するため、目的に応じた適切なデータ選択が不可欠です。

例を挙げると、「製品の新機能を市場に投入するタイミングを決定したい」というビジネス目的があるとします。この場合、市場のトレンド、競合の動向、顧客の需要変動などが影響する可能性があります。従って、過去2年間の同様の製品の月別売上高、マーケットシェア、顧客からのフィードバックデータ、競合製品の発売時期や市場反応などのデータを集めることになります。

分析では、新機能の市場投入時期を決めるために、これらの変数間の関係性を探り、特に売上高とマーケットシェアの変動パターンを深堀りします。たとえば、X=市場のニーズやトレンドの指標、Y=売上高とマーケットシェアの増減として、これらの因子の相関関係を分析することが考えられます。ここで重要なのは、過去のデータに基づいて未来を予測する際の傾向と、その傾向が新機能の投入タイミングにどう影響するかを理解することです。

このように、目的を明確に設定し、それに基づいたデータを選定して分析を行うことで、単なるデータの集計を超えた、戦略的な意思決定を支援する洞察を得ることができます。結果的に、データ分析はビジネスにおけるリスクの軽減、機会の最大化、そして競争優位性の確保に直結する重要なプロセスとなるのです。

（５）分析データの種類

正解

正解: B. 自動車のブランド

解説:
カテゴリデータは、数値ではなく、項目やグループによってデータを分類するときに用いられます。自動車のブランド（例: トヨタ、ホンダ、テスラ）のように、データが特定のカテゴリーやグループに属している場合にカテゴリデータとなります。これは数値ではなく、テキストやラベルで表されます。一方、市の人口や年収のようなデータは数値で表され、量的な情報を提供するため、数値データに該当します。数値データは数学的な操作や計算が可能なデータです。

---

データ分析の世界に足を踏み入れると、私たちは主に2種類のデータに出会います。理解しやすくするために、これらのデータを日常生活から引き出された例を用いて説明しましょう。

数値データ

まず、第一のタイプは数値データです。数値データは、1、2、3といった数値で表され、私たちの日常で頻繁に遭遇します。たとえば、お財布に入っているお金の総額、部屋の長さや重さを計る時、または友人との待ち合わせ時間の計画などです。さらに、アンケート調査でよく見る5段階評価（たとえば、全く満足しないから非常に満足するまで）も、数値データの一例です。これらのデータは、足したり引いたりすることで総和や差を出すことができるだけでなく、平均値を計算して全体の傾向を見たり、標準偏差を求めてデータがどの程度バラついているかを把握することも可能です。

カテゴリーデータ

第二のタイプは、性別や血液型、あるいは商品のバーコードのように、特定のカテゴリーに分類されるデータです。これらは、具体的な数値による量を表すのではなく、属性や性質を表します。例えば、「男性」や「女性」というカテゴリーや、「A型」、「B型」といった血液型です。商品のバーコードも、それぞれが異なる商品を識別するための一意のコードとして機能し、カテゴリーデータの一例となります。また、郵便番号や電話番号も数字の並びで表されますが、これらは単なる数値ではなく、特定の住所や電話回線を指し示すユニークな識別子として機能します。これらのデータは、それぞれが属するカテゴリーごとに数え上げることで、どのカテゴリーがどれだけ存在するかを知ることが基本的な分析方法となります。

これらの違いを理解することで、データをより深く掘り下げ、有意義な洞察を得るための第一歩を踏み出すことができます。数値データには計算を用いてより詳細な分析が可能であり、カテゴリーデータではデータの分布や傾向を把握することができます。これらの基本的な違いを抑えることで、データ分析の世界が一段と理解しやすくなるでしょう。

2．数量データの基礎集計

（１）代表値（平均,中央値,最頻値）

代表値とは、データの中心的な傾向や典型的な値を示す統計量のことを指します。代表値には、主に以下の3つがあります。

1. 平均値 (Mean)
2. 中央値 (Median)
3. 最頻値 (Mode)

1. 平均値 (Mean)

定義: データの総和をデータの個数で割った値です。

計算方法: 全てのデータの値を合計し、その合計をデータの個数で割ります。

例: データが 3,5,7,9,113, 5, 7, 9, 113,5,7,9,11 の場合、 平均値=3+5+7+9+115=355=7\text{平均値} = \frac{3 + 5 + 7 + 9 + 11}{5} = \frac{35}{5} = 7平均値=53+5+7+9+11​=535​=7

特徴:

• 全データの影響を受けやすく、外れ値（極端に大きい値や小さい値）によって変動しやすいです。

2. 中央値 (Median)

定義: データを小さい順または大きい順に並べたとき、ちょうど中央に位置する値です。

計算方法: データを昇順または降順に並べ替え、その中央の値を取ります。データの個数が偶数の場合、中央の2つの値の平均を取ります。

例: データが 3,5,7,9,113, 5, 7, 9, 113,5,7,9,11 の場合、

• 並べ替え後: 3,5,7,9,113, 5, 7, 9, 113,5,7,9,11
• 中央値は 7

データが 3,5,7,93, 5, 7, 93,5,7,9 の場合、

• 並べ替え後: 3,5,7,93, 5, 7, 93,5,7,9
• 中央の2つの値は 5 と 7 なので、その平均を取ります。 中央値=5+72=6\text{中央値} = \frac{5 + 7}{2} = 6中央値=25+7​=6

特徴:

• 外れ値の影響を受けにくく、データの中心をより適切に表すことができます。

3. 最頻値 (Mode)

定義: データの中で最も頻繁に現れる値です。

計算方法: 各データの出現回数を数え、その中で最も多く現れる値を取ります。

例: データが 3,5,7,7,9,113, 5, 7, 7, 9, 113,5,7,7,9,11 の場合、

• 7 が最も多く現れるので、最頻値は 7

データが 3,5,7,9,113, 5, 7, 9, 113,5,7,9,11 の場合、

• 全ての値が一度しか現れないので、最頻値は存在しない（または全てが最頻値）。

特徴:

• データの山（モード）を示し、データの分布の特徴を表すのに有効です。データが多峰性の場合、複数の最頻値を持つことがあります。

まとめ

• 平均値はデータ全体の傾向を表しますが、外れ値の影響を受けやすいです。
• 中央値はデータの中心を表し、外れ値の影響を受けにくいです。
• 最頻値はデータの中で最もよく現れる値を示し、データの分布の特徴を捉えるのに役立ちます。

これらの代表値を組み合わせて使用することで、データの全体的な傾向や分布をよりよく理解することができます。

（２）ばらつきの指標 標準偏差

標準偏差とは？

標準偏差 (Standard Deviation) は、データが平均からどの程度散らばっているか、つまりばらつきを示す指標です。標準偏差が小さいほど、データが平均値に近いところに集中しており、標準偏差が大きいほど、データが平均値から遠くに散らばっていることを意味します。

標準偏差の計算方法

標準偏差の計算は以下の手順で行います。

1. 平均値 (Mean) を計算する。
2. 各データと平均値の差を求める。
3. 差の二乗を計算する。
4. 二乗した値の平均を求める（これを分散という）。
5. 分散の平方根を取る。

計算例

データセット：3,5,7,9,113, 5, 7, 9, 113,5,7,9,11

1. 平均値の計算: 平均値=3+5+7+9+115=7\text{平均値} = \frac{3 + 5 + 7 + 9 + 11}{5} = 7平均値=53+5+7+9+11​=7
2. 各データと平均値の差: (3−7),(5−7),(7−7),(9−7),(11−7)(3-7), (5-7), (7-7), (9-7), (11-7)(3−7),(5−7),(7−7),(9−7),(11−7) −4,−2,0,2,4-4, -2, 0, 2, 4−4,−2,0,2,4
3. 差の二乗: (−4)2,(−2)2,02,22,42(-4)^2, (-2)^2, 0^2, 2^2, 4^2(−4)2,(−2)2,02,22,42 16,4,0,4,1616, 4, 0, 4, 1616,4,0,4,16
4. 二乗した値の平均（分散）: 分散=16+4+0+4+165=405=8\text{分散} = \frac{16 + 4 + 0 + 4 + 16}{5} = \frac{40}{5} = 8分散=516+4+0+4+16​=540​=8
5. 分散の平方根（標準偏差）: 標準偏差=8≈2.83\text{標準偏差} = \sqrt{8} \approx 2.83標準偏差=8​≈2.83

標準偏差の特徴

• 単位: 元のデータと同じ単位で表されます。これにより、ばらつきの程度を直感的に理解しやすくなります。
• 分布の形状: データが正規分布に従う場合、標準偏差は分布の広がりを示します。例えば、正規分布においてデータの約68%が平均値から±1標準偏差の範囲内に収まります。
• 外れ値の影響: 標準偏差は外れ値の影響を受けやすいため、データに外れ値がある場合は注意が必要です。

実際の利用例

• 品質管理: 工業製品の品質管理において、製品の寸法や重量などが規格値からどの程度ばらついているかを評価するのに使われます。
• リスク評価: 金融において、投資のリスクを評価するために標準偏差が使われます。リターンの標準偏差が大きいほど、投資のリスクが高いことを意味します。
• データ分析: 科学や社会科学の研究において、データのばらつきを評価するために標準偏差が広く使われます。

まとめ

標準偏差は、データのばらつきを定量的に示す重要な指標です。データの平均からの散らばり具合を理解することで、データの特性や傾向をより深く把握することができます。

（３）数量データの分析

（４）母集団と標本

なぜ、視覚化が大切なのか？

数値だけ見ていたのでは本質を見誤る。

（５）箱ひげ図

箱ひげ図（はこひげず）は、データの分布を視覚的に表すためのグラフの一つです。

箱ひげ図の構造

1. 箱（ボックス）
   • 箱の中央の線: データの中央値（中央値）を表します。データを小さい順に並べたとき、ちょうど真ん中にくる値です。
   • 箱の上下の境界: 第1四分位数（Q1）と第3四分位数（Q3）を表します。第1四分位数はデータの下位25%の位置にある値、第3四分位数はデータの上位25%の位置にある値です。
   • 箱の高さ: 箱の上下の境界の間の距離は四分位範囲（IQR）と呼ばれ、データの中央50%がどれくらい広がっているかを示します。
2. ひげ（ウィスカー）
   • 箱から上下に伸びる線で、データの範囲を示します。ひげの先端は、通常、データの最小値と最大値を表します。ただし、ひげの長さは通常、Q1から1.5倍のIQRまで、Q3から1.5倍のIQRまでと定義され、それ以上のデータ点は外れ値（アウトライア）として別途プロットされます。
3. 外れ値（アウトライア）
   • ひげの範囲外にあるデータ点は、小さな円や星などの記号で表示されます。

箱ひげ図の読み方

• 中央値: データの中央の値なので、データがどの辺りに集中しているかがわかります。
• 四分位範囲（IQR）: データのばらつきを示します。IQRが大きいほど、データの広がりが大きいことを示します。
• ひげの長さ: データの全体の範囲を示します。ひげが長いと、データのばらつきが大きいことを示します。
• 外れ値: データの中でも特に小さいか大きい値で、他のデータ点から離れています。

例

例えば、クラスのテストの点数を箱ひげ図で表すとします。

1. 箱の中央の線: 中央のテストの点数。
2. 箱の上下の境界: テストの点数の上位25%と下位25%の点数の範囲。
3. ひげ: 最低点と最高点。
4. 外れ値: 他の点数から大きく離れている特別に高い点数や低い点数。

箱ひげ図を使うと、クラス全体の点数の傾向やばらつきを簡単に視覚的に理解することができます。

（６）ヒストグラム

ヒストグラムとは？

ヒストグラムは、データの分布を視覚的に示すための棒グラフの一種です。データがどのように分散しているかを理解するのに役立ちます。

ヒストグラムの作り方

ヒストグラムを作るためには、まずデータを集めて、それをいくつかの区間（ビンと呼ばれます）に分けます。そして、それぞれの区間に含まれるデータの数を数えて、その数を棒グラフとして描きます。

例：テストの点数

クラスのテストの点数が以下の通りだとします：

• 55, 60, 65, 70, 75, 80, 85, 90, 95, 100

1. データを区間に分ける

• 50-59点: 1人
• 60-69点: 2人
• 70-79点: 2人
• 80-89点: 2人
• 90-100点: 3人

1. 棒グラフを描く

• 横軸に区間（50-59, 60-69, …）
• 縦軸に人数（1人, 2人, …）

ヒストグラムの読み方

ヒストグラムを見ると、どの区間に多くのデータが集まっているかが一目でわかります。例えば、上の例だと、90-100点の区間に最も多くの生徒がいることがわかります。

ヒストグラムの特徴

1. ビンの幅：区間の幅を広くしたり狭くしたりすることで、ヒストグラムの形が変わります。幅が広いと大まかな分布がわかり、幅が狭いと詳細な分布がわかります。
2. 高さ：棒の高さは、その区間に含まれるデータの数を表します。高さが高いほど、その区間に多くのデータが集まっていることを示します。
3. 形：ヒストグラムの形を見ることで、データがどのように分布しているか（例えば、均等に分布しているか、偏っているか）がわかります。

まとめ

ヒストグラムは、データの分布を視覚的に理解するための便利なツールです。区間に分けてデータの数を数えるだけで、簡単に作成できます。これを使うことで、データがどのように分布しているかを一目で把握することができます。

（７）データの基準化と偏差値

3．カテゴリーデータの基礎集計

（１）カテゴリーデータの集計

（２）ピボットテーブルの基本操作

Excelでピボットテーブルを作成する手順について、詳細に解説します。

ピボットテーブルの作成手順（Excelの場合）

1. データの準備

ピボットテーブルを作成するためのデータが適切に整理されていることを確認します。データは表形式で、各列に明確なヘッダーが必要です。

例: 売上データ

日付	商品	売上	地域
2024-01-01	商品A	1000	東京
2024-01-01	商品B	1500	大阪
2024-01-02	商品A	2000	東京
2024-01-02	商品B	2500	大阪

2. データ範囲の選択

ピボットテーブルを作成したいデータ範囲を選択します。データ全体を選択することを忘れないようにしましょう。

3. ピボットテーブルの挿入

1. 「挿入」タブをクリックします。
2. 「ピボットテーブル」を選択します。
3. 「ピボットテーブルの作成」ダイアログが表示されます。

4. ピボットテーブルの配置場所を選択

• データ範囲が正しく選択されていることを確認します。
• ピボットテーブルを配置する場所を選択します。新しいワークシートまたは既存のワークシートのいずれかを選びます。
• 「OK」をクリックします。

5. ピボットテーブルの構成

ピボットテーブルを挿入すると、右側に「ピボットテーブル フィールド」ウィンドウが表示されます。このウィンドウで、データフィールドをドラッグアンドドロップしてピボットテーブルを構成します。

• 行（Rows）:
• 行ラベルとして使用するフィールドをドラッグします。
• 例: 「商品」を行にドラッグ
• 列（Columns）:
• 列ラベルとして使用するフィールドをドラッグします。
• 例: 「日付」を列にドラッグ
• 値（Values）:
• 集計するフィールドをドラッグします。通常、数値フィールドがここに配置されます。
• 例: 「売上」を値にドラッグ
• デフォルトでは、売上の合計（Sum）が表示されます。必要に応じて、他の集計方法（平均、カウントなど）を選択できます。
• フィルター（Filters）:
• ピボットテーブルのデータをフィルタリングするためのフィールドをドラッグします。
• 例: 「地域」をフィルターにドラッグ（必要に応じて）

6. ピボットテーブルの結果

フィールドを適切に配置すると、ピボットテーブルが自動的に生成されます。先ほどの例に基づくと、以下のようなピボットテーブルが作成されます。

例:

商品	2024-01-01	2024-01-02
商品A	1000	2000
商品B	1500	2500

まとめ

ピボットテーブルは、データを迅速かつ柔軟に集計・分析するための非常に便利なツールです。Excelでの基本的な操作手順を理解し、実践することで、データから有益な情報を引き出すことができるようになります。

（３）単純集計とクロス集計の演習

（４）単純集計とグラフ

（５）母比率の推定

母比率の推定を簡単な例を使って説明します。母比率の推定とは、全体の中でどのくらいの割合のものがあるかを、サンプル（全体の一部）を使って予測することです。

例：キャンディの袋

あなたは、キャンディがたくさん入っている大きな袋を持っています。この袋の中には赤いキャンディと青いキャンディが入っています。でも、袋が大きすぎて全部を数えるのは大変です。そこで、袋の中のキャンディのうち、どれくらいが赤いキャンディなのかを知りたいとします。

サンプルを取る

まず、袋の中から無作為に100個のキャンディを取り出してみます。これが「サンプル」です。サンプルは全体を代表する小さな部分です。

サンプルの結果

100個のキャンディのうち、60個が赤いキャンディ、40個が青いキャンディだったとします。

• 赤いキャンディ：60個
• 青いキャンディ：40個

ここで、サンプルの中で赤いキャンディの割合を計算します。これを「サンプル比率」と呼びます。

サンプル比率 = 赤いキャンディの数 / サンプルの総数 サンプル比率=60100=0.6\text{サンプル比率} = \frac{60}{100} = 0.6サンプル比率=10060​=0.6

つまり、サンプルの中では60%が赤いキャンディです。

母比率の推定

袋の中全体の赤いキャンディの割合（これを「母比率」と言います）を予測するために、このサンプル比率を使います。ここでは、サンプル比率0.6を使って、袋全体のキャンディの60%が赤いキャンディであると推定します。

信頼区間

ただし、サンプルは袋全体を完全には表していないかもしれません。そこで、私たちは「信頼区間」というものを使って、母比率の範囲を示します。信頼区間は、「本当の母比率がこの範囲内にあるはずだ」という予測の範囲です。

例えば、サンプルサイズが100でサンプル比率が0.6の場合、よく使われる95%の信頼区間を計算すると、およそ0.5から0.7の間になります。これは、「袋全体の赤いキャンディの割合は50%から70%の間にあるだろう」と予測することを意味します。

まとめ

1. 母比率の推定とは、全体の中で特定のものがどれくらいの割合であるかをサンプルを使って予測することです。
2. サンプルを取って、その中の比率を計算します。これがサンプル比率です。
3. サンプル比率を使って、全体の割合（母比率）を推定します。
4. 信頼区間を使って、その推定の範囲を示します。

このようにして、母比率を推定することで、全体の状況を予測することができます。キャンディの例では、袋全体の赤いキャンディの割合を知ることができました。

信頼区間

信頼区間とは、データから得られた統計量（例えば、平均や比率）を使って、その真の値がどの範囲にあるかを推測する方法です。簡単に言うと、「この範囲内に本当の値があるはずだ」と自信を持って言える範囲のことです。これを中学生にもわかりやすく説明するために、例を使って解説します。

例：クラスの平均身長

あなたのクラスの平均身長を調べたいとします。でも、クラス全員の身長を測るのは大変なので、クラスの一部の生徒を選んでその平均身長を使ってクラス全体の平均身長を推測します。

サンプルの取得

まず、クラス全員のうち10人をランダムに選んで、その身長を測ります。次に、測った身長の平均を計算します。例えば、10人の平均身長が160cmだったとします。

サンプル平均と信頼区間

このサンプル平均160cmを使って、クラス全体の平均身長を推測します。でも、選んだ10人が特別に背が高いか低いかもしれないので、単に160cmだけではなく、信頼区間を使ってその推測の範囲を示します。

標準誤差の計算

信頼区間を計算するためには、標準誤差というものが必要です。標準誤差は、サンプルのばらつきを示すもので、標準偏差をサンプルサイズの平方根で割ったものです。

例えば、選んだ10人の標準偏差が5cmだったとします。 標準誤差=標準偏差サンプルサイズ=510≈1.58\text{標準誤差} = \frac{\text{標準偏差}}{\sqrt{\text{サンプルサイズ}}} = \frac{5}{\sqrt{10}} \approx 1.58標準誤差=サンプルサイズ​標準偏差​=10​5​≈1.58

信頼区間の計算

一般的に、95%の信頼区間を使います。これは、「95%の確率で真の平均身長がこの範囲内にある」と言える範囲です。

信頼区間の計算には、サンプル平均に標準誤差の1.96倍を加えたり引いたりします。 信頼区間=サンプル平均±1.96×標準誤差\text{信頼区間} = \text{サンプル平均} \pm 1.96 \times \text{標準誤差}信頼区間=サンプル平均±1.96×標準誤差

具体的に計算すると： 信頼区間=160±1.96×1.58\text{信頼区間} = 160 \pm 1.96 \times 1.58信頼区間=160±1.96×1.58 信頼区間=160±3.1\text{信頼区間} = 160 \pm 3.1信頼区間=160±3.1

つまり、信頼区間は： 156.9cmから163.1cm156.9 \text{cm} \text{から} 163.1 \text{cm}156.9cmから163.1cm

解釈

この信頼区間は、「クラス全体の平均身長は、95%の確率で156.9cmから163.1cmの間にある」と言えます。これにより、サンプルから得られた平均がどの程度信頼できるかを示すことができます。

まとめ

• 信頼区間：データから得られた統計量を使って、その真の値がどの範囲にあるかを示す方法。
• 標準誤差：サンプルのばらつきを示し、信頼区間の計算に使います。
• 信頼区間の計算：サンプル平均に標準誤差の1.96倍を加えたり引いたりして計算します（95%の信頼区間の場合）。

信頼区間を使うと、サンプルデータから得られる推測の精度を示すことができ、より確かな判断ができます。

（６）クロス集計のポイント

4．確率分布

（１）確率分布とは（ビジネスでの用途）

確率分布とは、ある出来事がどのくらいの確率で起こるかを示すものです。中学生にもわかりやすいように、例を使って説明します。

例：サイコロの確率分布

サイコロを投げるとき、出る目の数は1から6までのどれかです。このとき、各目が出る確率は同じです。それぞれの目が出る確率をまとめたものが「確率分布」です。

サイコロの確率分布

• サイコロの目1が出る確率：1/6
• サイコロの目2が出る確率：1/6
• サイコロの目3が出る確率：1/6
• サイコロの目4が出る確率：1/6
• サイコロの目5が出る確率：1/6
• サイコロの目6が出る確率：1/6

このように、サイコロの出る目の数とそれぞれの確率を一覧にしたものが確率分布です。

確率分布のグラフ

確率分布はグラフでも表すことができます。例えば、サイコロの確率分布を棒グラフで表すと、次のようになります：

サイコロの目	確率
1	1/6
2	1/6
3	1/6
4	1/6
5	1/6
6	1/6

例：テストの点数の確率分布

今度は、テストの点数を考えてみましょう。例えば、クラスのテストの点数を調べて、次のような分布があったとします：

• 90点以上：10人
• 80点以上90点未満：20人
• 70点以上80点未満：15人
• 60点以上70点未満：5人
• 60点未満：5人

この場合、それぞれの点数範囲の確率を求めると、次のような確率分布になります：

• 90点以上：10 / 55 = 0.182（18.2%）
• 80点以上90点未満：20 / 55 = 0.364（36.4%）
• 70点以上80点未満：15 / 55 = 0.273（27.3%）
• 60点以上70点未満：5 / 55 = 0.091（9.1%）
• 60点未満：5 / 55 = 0.091（9.1%）

確率分布はビジネスのさまざまな場面で利用され、意思決定やリスク管理に役立ちます。中学生にもわかりやすいように、具体的な例を使って説明します。

例1：売上予測

企業は、製品の売上を予測するために確率分布を使います。

シナリオ

あるお菓子メーカーが、新しいクッキーを発売しようとしています。マーケティングチームは、過去のデータを使って次のような売上の確率分布を作成しました。

• 低売上（1,000箱未満）：20%の確率
• 中売上（1,000箱〜5,000箱）：50%の確率
• 高売上（5,000箱以上）：30%の確率

利用方法

この確率分布を使って、会社はどのくらいの材料を仕入れるべきか、どのくらいの広告費をかけるべきかを決定します。例えば、売上が高い可能性が高いなら、広告を増やしたり、製品の在庫を多めに用意したりします。

例2：在庫管理

確率分布は在庫管理にも役立ちます。

シナリオ

ある本屋さんが、人気の本の在庫を管理する必要があります。過去の販売データから次のような確率分布を作成しました。

• 1日あたりの販売数
  • 1冊：10%の確率
  • 2冊：20%の確率
  • 3冊：40%の確率
  • 4冊：20%の確率
  • 5冊：10%の確率

利用方法

この確率分布を使って、本屋さんは適切な在庫を確保します。例えば、毎日平均して3冊売れる確率が高いので、常に少なくとも3冊の在庫を持っておくようにします。これにより、在庫切れのリスクを減らし、売上を最大化します。

例3：マーケティングキャンペーンの効果測定

企業はマーケティングキャンペーンの効果を予測するために確率分布を使います。

シナリオ

あるオンラインショップが、割引キャンペーンを実施しました。過去のキャンペーンデータを分析し、次のような確率分布を作成しました。

• 低反応（売上の10%増加）：30%の確率
• 中反応（売上の20%増加）：50%の確率
• 高反応（売上の30%増加）：20%の確率

利用方法

この確率分布を使って、オンラインショップはキャンペーンの期待効果を予測し、予算を適切に配分します。例えば、売上が20%増加する確率が最も高いので、その前提で予算を設定し、キャンペーンを実施します。

まとめ

確率分布は、ビジネスにおいて重要な意思決定を行うための強力なツールです。売上予測、在庫管理、マーケティングキャンペーンの効果測定など、さまざまな場面で利用されます。確率分布を理解し利用することで、企業はリスクを管理し、効率的な運営を実現することができます。

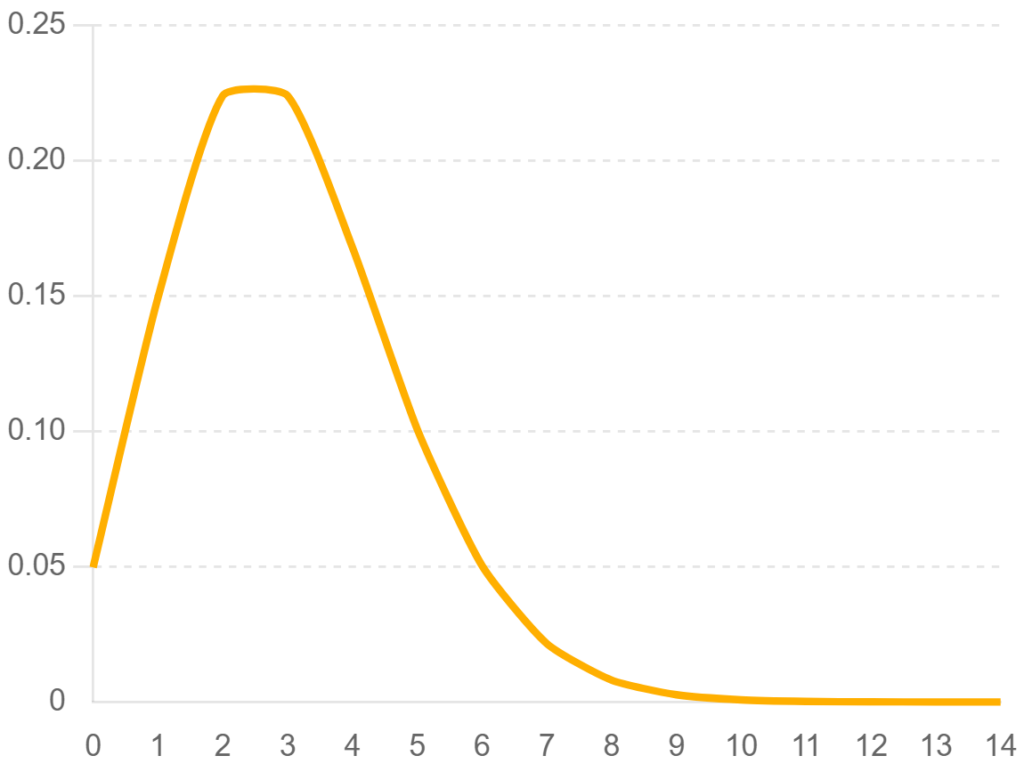
（２）ポアソン分布

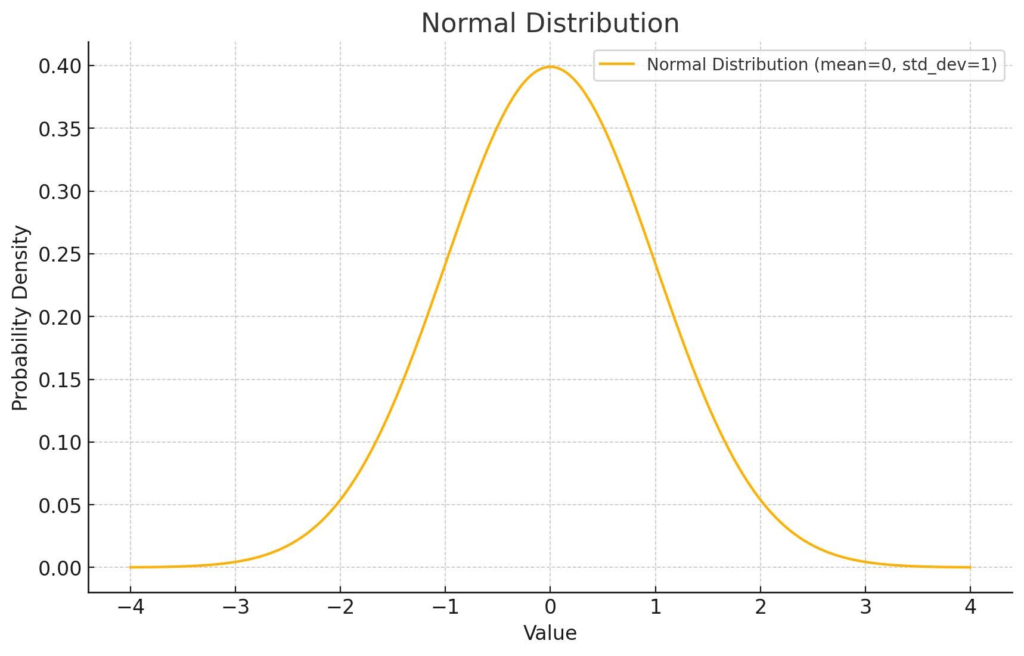
（３）正規分布

正規分布とは？

正規分布は、データが平均値を中心に左右対称に分布する形をしたグラフのことです。これは、たくさんのデータが集まるときに自然と現れる形の一つです。正規分布のグラフは、山のような形をしていて、これを「ベルカーブ」とも呼びます。

正規分布の特徴

1. 平均値（μ）：グラフの中心にある値で、データの平均です。
2. 標準偏差（σ）：データが平均値の周りにどれくらい広がっているかを示す値です。標準偏差が小さいとデータが平均値の近くに集まり、大きいと広がります。

例：テストの点数

クラスのテストの点数を例に考えてみましょう。クラス全体の平均点が70点で、ほとんどの生徒が60点から80点の間に点数があるとします。

1. 平均値（μ）：70点
2. 標準偏差（σ）：10点（これは、点数がどれくらい広がっているかを示します）

正規分布のグラフ

• 中心の高さ：平均値（70点）のところが一番高くなります。
• 左右対称：平均値を中心に左右対称に広がります。
• 両端が細くなる：平均値から離れるほど、データの数が少なくなるので、グラフの両端は細くなります。

正規分布の応用

正規分布は、たくさんの実際のデータに当てはまります。例えば：

• 身長：多くの人の身長を集めると、平均身長の周りに左右対称に広がる。
• テストの点数：たくさんのテストの点数を集めると、平均点の周りに広がる。

正規分布の重要性

1. データの予測：正規分布を使うと、データがどのように分布するかを予測できます。
2. 異常値の発見：データが平均値から大きく外れる場合、そのデータが異常かどうかを判断できます。
3. 統計分析：データの分析や解釈に役立ちます。

まとめ

正規分布は、データが平均値を中心に左右対称に分布する形をしたグラフです。身近な例として、テストの点数や身長など、多くのデータが正規分布に従います。この分布を理解すると、データの特徴をつかみやすくなり、統計分析や予測に役立ちます。

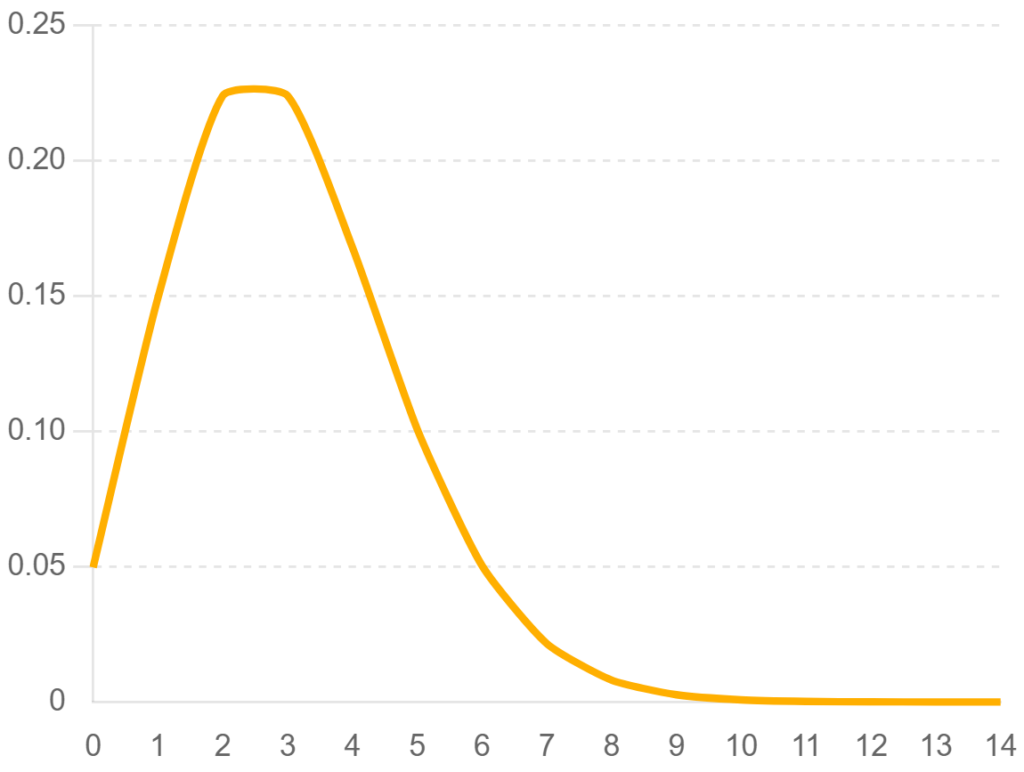
（４）二項分布

二項分布とは？

二項分布は、ある試行を何回か繰り返したときに、特定の結果が何回出るかを表す分布です。この試行は、成功か失敗かのどちらかしかない場合に使います。二項分布の名前の由来です。

例：コイン投げ

コインを投げたとき、表が出るか裏が出るかのどちらかです。例えば、コインを10回投げて、表が5回出る確率を知りたいとします。このような場合に二項分布を使います。

二項分布の特徴

1. 試行回数（n）：試行を何回行うか。
2. 成功確率（p）：1回の試行で成功する確率。
3. 成功回数（k）：成功する回数。

二項分布の計算方法

二項分布の確率を計算する公式は以下の通りです。

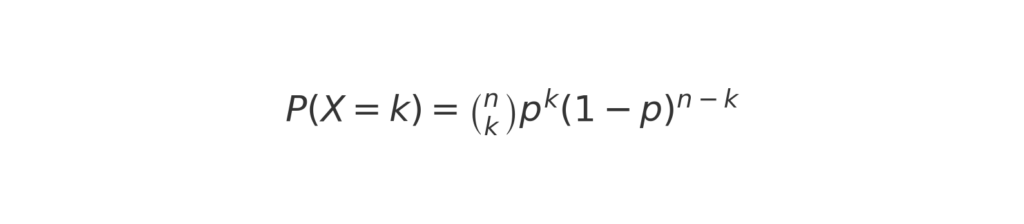
ここで、

• (\binom{n}{k}) は組み合わせの数で、「n回の試行でk回成功する場合の数」です。
• (p) は成功の確率。
• (1-p) は失敗の確率。
• (n-k) は失敗する回数。

実際の例

コインを10回投げて、表が3回出る確率を計算してみましょう。コイン投げの成功確率（表が出る確率）は0.5です。

この計算をすると、次のような数式になります。

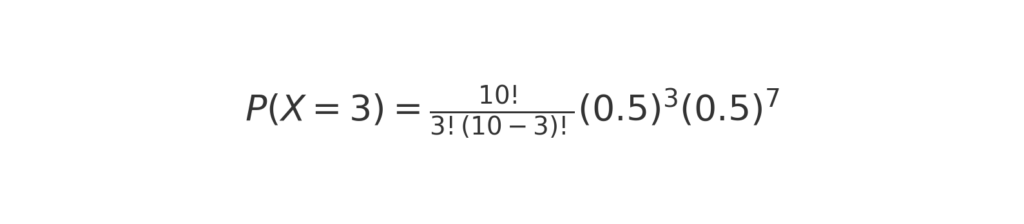
したがって、コインを10回投げて表が3回出る確率は約0.117、つまり11.7%です。

二項分布の特徴

• 離散的な分布：結果が離散的（具体的な数値）です。
• 試行が独立：各試行が独立している（1回の結果が次の結果に影響しない）ことが前提です。
• 二項試行：成功か失敗かの2つの結果しかない試行です。

まとめ

二項分布は、成功か失敗かのどちらかしかない試行を何回も繰り返したときに、特定の結果が何回出るかを表す分布です。コイン投げのようなシンプルな例から、もっと複雑な例まで、さまざまな場合に応用できます。

5．有意差の検定

（１）母平均の有意差検定

母平均の有意差検定は、ある母集団の平均が特定の値と異なるかどうかを検証するための統計的手法です。具体的には、次の手順で行われます。

手順

1. 帰無仮説と対立仮説の設定:

• 帰無仮説 (H₀): 母平均 μ は特定の値 μ₀ と等しい。
• 対立仮説 (H₁): 母平均 μ は特定の値 μ₀ と異なる（片側検定の場合は「大きい」または「小さい」と異なる）。

1. 検定統計量の計算:

• 標本平均 (\bar{x})、標本の標準偏差 s、標本サイズ n を用いて、t値またはz値を計算します。母標準偏差が分かっている場合はz検定、分からない場合はt検定を使用します。
• z値の計算:
  [
  z = \frac{\bar{x} - \mu_0}{\frac{\sigma}{\sqrt{n}}}
  ]
• t値の計算:
  [
  t = \frac{\bar{x} - \mu_0}{\frac{s}{\sqrt{n}}}
  ]

1. 臨界値の決定:

• 選択した有意水準（通常は5%や1%）に基づいて、標準正規分布またはt分布から臨界値を求めます。

1. p値の計算:

• 計算した検定統計量に基づいて、p値を求めます。p値は、帰無仮説が真であると仮定した場合に、観測されたデータがどれだけ極端であるかを示します。

1. 結論:

• p値が有意水準よりも小さい場合、帰無仮説を棄却します。つまり、母平均が特定の値と有意に異なると判断されます。
• p値が有意水準以上の場合、帰無仮説を棄却しません。つまり、母平均が特定の値と異なるとは言えないと判断されます。

具体例

ある新薬の効果を調べるために、患者に薬を投与し、症状の改善度を調査したとします。過去のデータでは、従来薬の平均改善度が50点でした。この新薬の平均改善度が従来薬と異なるかどうかを検証します。

1. 帰無仮説:
   [
   H_0: \mu = 50
   ]
   対立仮説:
   [
   H_1: \mu \neq 50
   ]
2. 標本データ: 新薬の標本平均 (\bar{x} = 55)、標本の標準偏差 (s = 10)、標本サイズ (n = 30)
3. t値の計算:
   [
   t = \frac{55 - 50}{\frac{10}{\sqrt{30}}} = \frac{5}{1.83} \approx 2.73
   ]
4. 臨界値: 有意水準5%で自由度29のt分布の臨界値は約2.045
5. 結論: 計算したt値 2.73 は臨界値 2.045 を超えているため、帰無仮説を棄却します。新薬の平均改善度は従来薬の50点と有意に異なると判断されます。

このように、有意差検定を用いることで、母平均が特定の値と異なるかどうかを統計的に検証することができます。

（２）ｔ検定

t検定は、2つのグループの平均値がどれくらい異なるかを調べるための統計的方法です。例えば、「新しい勉強法を使ったクラス」と「従来の勉強法を使ったクラス」のテストの平均点が異なるかどうかを調べるのに使います。

例えを使った説明

勉強法の効果を調べる

想像してください。あなたが新しい勉強法を開発したとします。新しい勉強法が本当に効果があるかどうかを確認するために、2つのクラスで実験を行いました。

• クラスA：新しい勉強法を使った
• クラスB：従来の勉強法を使った

テストの結果を集めて、2つのクラスの平均点を比較します。

t検定のステップ

1. データを集める：クラスAとクラスBのテストの点数を集めます。
   • 例：クラスAの点数：85, 90, 78, 92, 88 クラスBの点数：80, 83, 77, 85, 82
2. 平均を計算する：それぞれのクラスの平均点を計算します。
   • クラスAの平均：86.6点
   • クラスBの平均：81.4点
3. 差を調べる：t検定を使って、これらの平均点の差が偶然か、それとも新しい勉強法の効果によるものかを調べます。

t検定の考え方

t検定は、「2つのグループの平均値の差が統計的に有意かどうか」を調べます。統計的に有意とは、「偶然ではなく、本当に差がある」ということです。

簡単なイメージ

もっと簡単に言うと、t検定は「2つのグループの結果が異なるかどうかを確かめるテスト」です。クラスAの平均点がクラスBの平均点よりも高い場合、その差が偶然の可能性が低ければ、新しい勉強法が効果的だと言えます。

まとめ

t検定は、2つのグループの平均値の差が本当に意味があるかどうかを調べるための統計的方法です。新しい勉強法の効果を確認するのに使ったり、他にもさまざまな分野で応用されます。

T検定の種類

1標本t検定

1標本t検定は、「あるグループの平均値が特定の値と異なるかどうか」を調べるための統計的方法です。例えば、クラスのテストの平均点が目標点数（例えば75点）と異なるかどうかを調べるのに使います。

例えを使った説明

クラスの平均点と目標点

想像してみてください。あなたのクラスでは、期末テストの平均点が75点以上であることを目標にしています。期末テストが終わり、クラス全体の点数を集めました。これらの点数から、クラスの平均点が75点以上かどうかを確認したいです。

1標本t検定のステップ

1. データを集める：クラスのテストの点数を集めます。
   • 例：点数：80, 85, 78, 92, 88
2. 平均を計算する：これらの点数の平均を計算します。
   • 平均：84.6点
3. 目標点数と比較する：1標本t検定を使って、この平均点が目標の75点と統計的に異なるかどうかを調べます。

t値とp値

1標本t検定では、計算されたt値と呼ばれる数字を使って、結果が偶然でないかどうかを判断します。さらに、p値という数字を使って、「この結果が偶然である可能性」を評価します。

• t値：データの平均と目標値の差を表す値。
• p値：結果が偶然である確率を示す値。通常、p値が0.05以下であれば、結果は統計的に有意とされます（つまり、偶然ではなく、意味のある差があると判断されます）。

簡単なイメージ

もっと簡単に言うと、1標本t検定は「クラスの平均点が目標点数と違うかどうかを確認するテスト」です。もしt検定の結果が統計的に有意であれば、クラスの平均点が目標点数と本当に異なることを示します。

まとめ

1標本t検定は、「あるグループの平均値が特定の値と異なるかどうか」を調べるための統計的方法です。クラスのテストの平均点が目標点数と異なるかどうかを確認するのに使ったり、他にもさまざまな分野で応用されます。

2標本t検定（独立t検定）

2標本t検定は、2つの異なるグループの平均値がどれくらい異なるかを調べるための統計的方法です。例えば、「新しい勉強法を使ったクラス」と「従来の勉強法を使ったクラス」のテストの平均点が異なるかどうかを調べるのに使います。

例えを使った説明

新しい勉強法と従来の勉強法

あなたが新しい勉強法を開発したとします。この勉強法が本当に効果があるかどうかを確認するために、2つのクラスで実験を行いました。

• クラスA：新しい勉強法を使った
• クラスB：従来の勉強法を使った

テストの結果を集めて、2つのクラスの平均点を比較します。

2標本t検定のステップ

1. データを集める：クラスAとクラスBのテストの点数を集めます。
   • 例：クラスAの点数：85, 90, 78, 92, 88 クラスBの点数：80, 83, 77, 85, 82
2. 平均を計算する：それぞれのクラスの平均点を計算します。
   • クラスAの平均：86.6点
   • クラスBの平均：81.4点
3. 差を調べる：2標本t検定を使って、これらの平均点の差が偶然か、それとも新しい勉強法の効果によるものかを調べます。

t値とp値

2標本t検定では、計算されたt値と呼ばれる数字を使って、結果が偶然でないかどうかを判断します。さらに、p値という数字を使って、「この結果が偶然である可能性」を評価します。

• t値：2つのグループの平均の差を表す値。
• p値：結果が偶然である確率を示す値。通常、p値が0.05以下であれば、結果は統計的に有意とされます（つまり、偶然ではなく、意味のある差があると判断されます）。

簡単なイメージ

もっと簡単に言うと、2標本t検定は「2つのグループの結果が異なるかどうかを確かめるテスト」です。クラスAの平均点がクラスBの平均点よりも高い場合、その差が偶然の可能性が低ければ、新しい勉強法が効果的だと言えます。

まとめ

2標本t検定は、2つの異なるグループの平均値の差が本当に意味があるかどうかを調べるための統計的方法です。新しい勉強法の効果を確認するのに使ったり、他にもさまざまな分野で応用されます。

対応のあるt検定（対応t検定）

対応のあるt検定は、「同じグループが2つの異なる条件でテストを受けたとき、その結果がどれくらい異なるか」を調べるための統計的方法です。例えば、クラス全体が新しい勉強法を試す前と後のテスト結果を比較するのに使います。

例えを使った説明

勉強法の効果を比較する

あなたが新しい勉強法を開発したとします。この勉強法が効果的かどうかを確認するために、クラス全体にテストを2回行いました。

• 1回目：新しい勉強法を試す前のテスト
• 2回目：新しい勉強法を試した後のテスト

対応のあるt検定のステップ

1. データを集める：同じ生徒が試した前後のテストの点数を集めます。
   • 例：1回目の点数：80, 85, 78, 92, 88 2回目の点数：85, 88, 82, 95, 90
2. 差を計算する：各生徒の前後の点数の差を計算します。
   • 差：5, 3, 4, 3, 2
3. 平均の差を調べる：対応のあるt検定を使って、これらの差の平均が偶然か、それとも新しい勉強法の効果によるものかを調べます。

t値とp値

対応のあるt検定では、計算されたt値と呼ばれる数字を使って、結果が偶然でないかどうかを判断します。さらに、p値という数字を使って、「この結果が偶然である可能性」を評価します。

• t値：2つの条件の差を表す値。
• p値：結果が偶然である確率を示す値。通常、p値が0.05以下であれば、結果は統計的に有意とされます（つまり、偶然ではなく、意味のある差があると判断されます）。

簡単なイメージ

もっと簡単に言うと、対応のあるt検定は「同じグループの結果が異なるかどうかを確かめるテスト」です。新しい勉強法を試す前と後で、点数が上がった場合、その差が偶然の可能性が低ければ、新しい勉強法が効果的だと言えます。

まとめ

対応のあるt検定は、「同じグループが異なる条件でテストを受けたとき、その結果の差が本当に意味があるかどうか」を調べるための統計的方法です。新しい勉強法の効果を確認するのに使ったり、他にもさまざまな分野で応用されます。

カイ二乗検定

カイ二乗検定とは？

カイ二乗検定は、データの集まりが偶然なのか、それとも何か特別な理由があるのかを確かめるための方法です。例えば、サイコロを投げたときに6がよく出るなら、そのサイコロが不正かどうかを確かめるために使うことができます。

例題：クラスの好きな色

あなたのクラスには30人の生徒がいます。彼らに好きな色を聞いて、次のような結果になったとします：

• 赤: 8人
• 青: 6人
• 緑: 10人
• 黄色: 6人

さて、この結果が「たまたまこうなった」だけなのか、それとも「何か理由がある」のかを確かめたいです。ここでカイ二乗検定を使います。

カイ二乗検定のステップ

1. 期待値の計算

• まず、各色が平均的に選ばれるならどうなるかを計算します。全員がランダムに色を選ぶと仮定すると、4つの色があるので、それぞれの色が選ばれる期待値は7.5人です。

1. 観察値と期待値の比較

• 実際の人数（観察値）：赤8人、青6人、緑10人、黄色6人
• 期待される人数（期待値）：赤7.5人、青7.5人、緑7.5人、黄色7.5人

1. 結果の解釈

• カイ二乗値が1.466という結果が出ました。次に、この値が「偶然の範囲内」なのか、それとも「偶然では説明できない」ほど大きいのかを判断する必要があります。これにはカイ二乗分布表を使いますが、簡単に言うと、この値がある基準値よりも小さい場合は「偶然の範囲内」と考えられます。

まとめ

カイ二乗検定は、データが偶然の結果なのかどうかを判断するためのツールです。クラスの好きな色の例を使って説明しましたが、他にもサイコロの公平性やアンケート結果の分析など、さまざまな場面で使うことができます。数学的な計算が含まれますが、基本的な考え方は「観察値と期待値の差を比較する」ことです。

回帰分析

まず、回帰分析を簡単な例えを使って説明します。

アイスクリームの売り上げと気温

あなたが夏休みにアイスクリームを売っているとしましょう。毎日、気温が高い日はたくさん売れて、気温が低い日はあまり売れないことに気づきました。この「気温」と「アイスクリームの売り上げ」の関係を知りたいと思ったとき、回帰分析が役立ちます。

回帰分析とは？

回帰分析は、あるデータ（ここでは気温）が他のデータ（アイスクリームの売り上げ）にどのような影響を与えるかを調べる方法です。具体的には、データの中から「どれくらいの気温の時にどれくらい売れるか」を予測するための数式を見つけます。

簡単なステップ

1. データを集める：まず、気温とアイスクリームの売り上げのデータを集めます。
   • 例：気温が30度の日に100個売れた、気温が25度の日に80個売れた、など。
2. グラフにする：集めたデータをグラフにします。
   • 横軸（X軸）には気温を、縦軸（Y軸）には売り上げを置きます。
3. 線を引く：データポイントを結ぶ最適な直線を引きます。この線は、気温と売り上げの関係を表します。

具体的なイメージ

例えば、以下のようなグラフを考えてみてください。

• 気温が20度の時は50個
• 気温が25度の時は80個
• 気温が30度の時は100個

これらのポイントをグラフにプロットして、それらを結ぶ直線を引きます。この直線は、気温が上がると売り上げも増えることを示しています。

数式の例

回帰分析の結果として得られる数式はこんな感じになります：

売り上げ=a×気温+b売り上げ = a \times 気温 + b売り上げ=a×気温+b

ここで、aとbはそれぞれの値によって決まる数字です。この数式を使うと、ある気温のときにどれくらい売れるかを予測できます。

まとめ

回帰分析は、「あるデータが他のデータにどのように影響するか」を調べるための方法です。簡単に言えば、アイスクリームの売り上げと気温のような関係を数式で表現し、将来の売り上げを予測することができます。

重回帰分析

重回帰分析を理解するために、もう一つの例を使います。

アイスクリームの売り上げと複数の要因

夏休みにアイスクリームを売っているとしましょう。今度は、アイスクリームの売り上げに影響を与える要因が気温だけでなく、他にもいくつかあることに気づきました。例えば、気温、降水量、そして宣伝の回数が売り上げに影響を与えているかもしれません。

重回帰分析とは？

重回帰分析は、複数のデータ（ここでは気温、降水量、宣伝の回数）が、他のデータ（アイスクリームの売り上げ）にどのような影響を与えるかを調べる方法です。つまり、単純な回帰分析が一つの要因と結果の関係を見るのに対して、重回帰分析は複数の要因と結果の関係を同時に見ます。

簡単なステップ

1. データを集める：まず、気温、降水量、宣伝の回数、そしてアイスクリームの売り上げのデータを集めます。
   • 例：気温が30度で、雨が降らなくて、宣伝を2回した日に100個売れた。
2. グラフにする：複数の変数があるため、グラフは3次元やそれ以上になりますが、基本的な考え方は同じです。
3. 数式を作る：データを元に、気温、降水量、宣伝の回数と売り上げの関係を示す最適な数式を見つけます。

数式の例

重回帰分析の結果として得られる数式はこんな感じになります：

売り上げ=a×気温+b×降水量+c×宣伝の回数+d売り上げ = a \times 気温 + b \times 降水量 + c \times 宣伝の回数 + d売り上げ=a×気温+b×降水量+c×宣伝の回数+d

ここで、a, b, c, dはそれぞれの値によって決まる数字です。この数式を使うと、ある気温、降水量、宣伝の回数のときにどれくらい売れるかを予測できます。

具体的なイメージ

例えば、以下のようなデータを考えてみてください：

• 気温が30度、降水量が0mm、宣伝の回数が2回のとき、売り上げは100個
• 気温が25度、降水量が10mm、宣伝の回数が1回のとき、売り上げは70個

これらのデータを元に、重回帰分析を使って数式を作ります。この数式を使うと、さまざまな条件のもとでの売り上げを予測できます。

まとめ

重回帰分析は、複数のデータが他のデータにどのように影響するかを調べるための方法です。気温、降水量、宣伝の回数など、複数の要因がアイスクリームの売り上げにどのように影響するかを数式で表現し、将来の売り上げを予測することができます。

多重共線性

先ほどのアイスクリームの売り上げの例をもう一度使います。アイスクリームの売り上げに影響を与える要因として、気温と降水量がありましたね。

気温と降水量の関係

夏の天気を思い出してください。気温が高い日（暑い日）は、一般的に降水量（雨の量）が少ないです。一方、気温が低い日（涼しい日）は、雨が降りやすいです。つまり、気温と降水量は互いに関連しています。

多重共線性とは？

このように、2つ以上の説明変数（ここでは気温と降水量）が強く関連していると、多重共線性が発生します。簡単に言うと、変数同士が似たような情報を持っていて、お互いに重なっている状態です。

多重共線性の問題点

多重共線性があると、次のような問題が発生します：

1. 予測が不安定になる：モデルの中の係数（数式の中のa, b, cなど）が大きく変動しやすくなり、予測の信頼性が低くなります。
2. 解釈が難しくなる：どの変数がどれくらい結果に影響を与えているのかがはっきりしなくなります。

簡単なイメージ

また、友達の例を使って説明します。

• 友達Aと友達Bがいつも一緒にいると、どちらが話しているのか分からなくなります。これは、友達Aと友達Bが強く関連しているためです。
• 同様に、気温と降水量が強く関連していると、どちらがアイスクリームの売り上げに影響を与えているのか分かりにくくなります。

多重共線性の対処法

多重共線性を解消するためには、いくつかの方法があります：

1. 変数を減らす：関連性の高い変数のうち、どちらか一方を取り除く。
2. 主成分分析（しゅせいぶんぶんせき）：複数の関連する変数をまとめて、新しい変数を作り出す方法です。
3. 変数選択法：統計的な手法を使って、影響の大きい変数だけを選び出す。

まとめ

多重共線性は、説明変数同士が強く関連している状態を指します。このため、予測が不安定になり、変数の影響を正確に理解することが難しくなります。対処するためには、変数を減らしたり、新しい変数を作り出す方法があります。

投稿者プロフィール

山崎講師代表取締役

セイ・コンサルティング・グループ株式会社代表取締役。
岐阜県出身。
2000年創業、2004年会社設立。
IT企業向け人材育成研修歴業界歴20年以上。
すべての無駄を省いた費用対効果の高い「筋肉質」な研修を提供します！
この記事に間違い等ありましたらぜひお知らせください。

最新の投稿

• 新入社員2024年11月23日「ゲシュタルト崩壊」とシステム開発
• 新入社員2024年11月23日データベースでテーブル名やフィールド名にスペースを使うことは、一般的には推奨されていません
• 新入社員2024年11月23日「データにはなぜ型が必要なのか？」を2進数の観点から解説
• 新入社員2024年11月23日ディスプレイの解像度の意味と変更方法