【初心者向け】物体検出の要!IoU(Intersection over Union)を徹底解説
こんにちは。ゆうせいです。
みなさんは、AIが画像を見て「ここに猫がいる!」とか「あそこに車がある!」と判断するとき、どうやってその 正確さ を採点しているか疑問に思ったことはありませんか?ただ単に「猫がいる」と当てるだけでは不十分で、画像の「どの場所に」「どのくらいの大きさで」いるかを正確に囲めていないといけませんよね。
今日は、そんな物体検出の世界で最も重要といっても過言ではない評価指標、IoUについて一緒に学んでいきましょう。難しそうな名前ですが、中身はとてもシンプルで面白いんですよ!
IoUってなに?
IoUとは Intersection over Union の略で、日本語では「和集合に対する共通部分の比率」なんて呼ばれたりします。少し難しそうな響きですよね。
簡単に言うと、これは AIが予測した枠 と 正解の枠 が、どれくらい重なっているかを表す数字です。
画像認識の世界では、見つけたい物体を四角い枠で囲みます。この枠のことを専門用語で バウンディングボックス と呼びます。AIが出したバウンディングボックスが、人間が用意した正解のバウンディングボックスとピタリと重なれば満点、全然違う場所にあれば0点。これを計算するのがIoUの役割です。
想像してみてください。あなたがクッキーの生地(正解の領域)に、クッキーの型(AIの予測)を押し当てるとします。生地と型がズレずにピッタリ重なれば気持ちいいですよね?その「ピッタリ度合い」を数値化したものがIoUなのです。
IoUの計算方法
では、具体的にどうやって計算するのでしょうか。高校数学で習った集合の図(ベン図)を思い出してみてください。2つの円が重なっている図です。
計算式は以下のようになります。
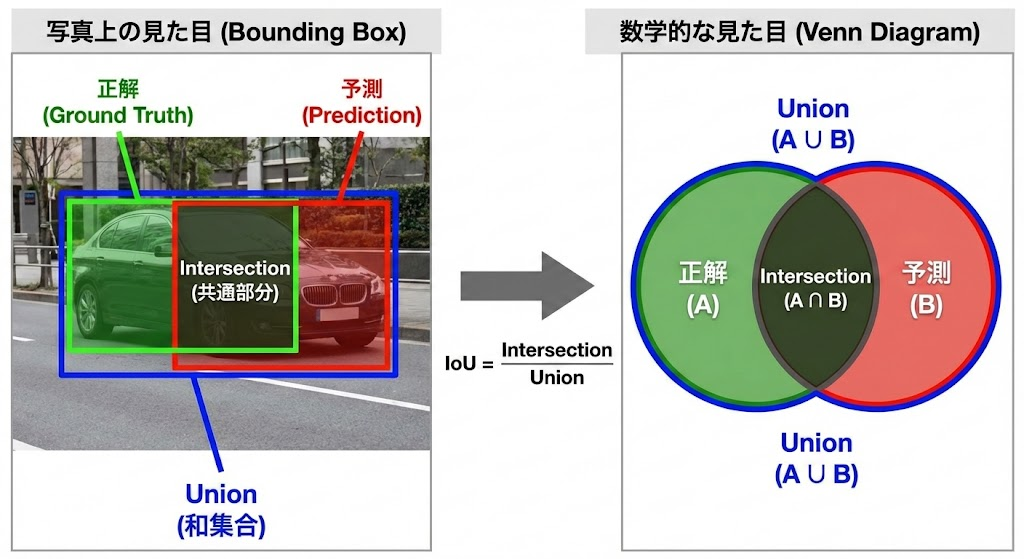
IoU = 2つの枠が重なっている部分の面積 ÷ 2つの枠を合わせた全体の面積
言葉だとイメージしにくいかもしれないので、もう少し分解してみましょう。ここには2つの四角形があります。
- AIが予測したバウンディングボックス(A)
- 正解のバウンディングボックス(B)
このとき、分子と分母は次のように考えます。
- 分子(Intersection):AとBが重なっている濃い部分の面積
- 分母(Union):AとBを全部足した面積(重なっている部分は1回だけ数えます)
もし、AとBが完全に一致していたらどうなるでしょうか?重なっている部分と全体の面積が同じになるので、答えは1になります。逆に、全く重なっていなければ、分子が0になるので、答えは0になります。
つまり、IoUは必ず0から1の間の数字になるんです。
どのくらいの数値なら「正解」なの?
IoUの値が出たとして、じゃあ何点以上なら「AIくん、よくできました!」と言えるのでしょうか。
一般的に、物体検出のタスクでは IoUが 0.5以上 であれば「正しく検出できた(True Positive)」と判断することが多いです。もちろん、より厳しい精度が求められる自動運転などの分野では、0.75やそれ以上の数値を基準にすることもあります。
0.5というと半分しか合っていないように聞こえるかもしれませんが、面積で半分重なっているというのは、見た目には結構しっかりと対象物を捉えている状態なんですよ。
IoUを使うメリットとデメリット
どんな指標にも良し悪しがあります。エンジニアとして、ここを理解しておくことはとても大切です。
メリット
まず、直感的でわかりやすいことです。 0から 1の間に収まるので、誰が見ても「精度が高い」「低い」が判断しやすいですよね。
また、画像のサイズや物体の大きさに依存しないのも大きな利点です。画面いっぱいの大きな象を検出する場合でも、遠くの小さな豆粒を検出する場合でも、重なり具合の 比率 で見るため、公平に評価ができます。これを スケール不変性 と言います。
デメリット
一方で、弱点もあります。それは、枠同士が全く重なっていない場合、どれだけ近くても遠くても、IoUはすべて 0になってしまうことです。
例えば、正解の枠のすぐ隣に予測枠がある場合と、画像の端っこにとんでもなく離れた場所に予測枠がある場合。人間から見れば「惜しい!」と「全然ダメ!」の違いがありますが、IoUにとってはどちらも等しく 0なのです。
これだと、AIが学習するときに「どっちの方向に修正すればいいか」がわからなくなってしまうんですね。これを専門的には 勾配消失問題 につながると言ったりします。
今後の学習の指針
ここまで読んでくれてありがとうございます!IoUが、単なる計算式ではなく、AIの「目」の良さを測るための大切な物差しであることがわかっていただけたでしょうか。
さて、ここからさらにステップアップするために、次は以下のキーワードについて調べてみることをおすすめします。
- GIoU (Generalized IoU):IoUのデメリットである「重ならないと学習が進まない問題」を解決した進化版です。
- DIoU / CIoU:さらに中心点の距離や、縦横比なども考慮に入れた、より高度な指標です。
- mAP (mean Average Precision):IoUを使って、モデル全体の性能を評価する総合的なスコアです。
まずはPythonなどのプログラミング言語を使って、自分で2つの四角形の座標からIoUを計算する関数を書いてみてください。手を動かすのが一番の近道ですよ。
それでは、また次の記事でお会いしましょう!
セイ・コンサルティング・グループでは新人エンジニア研修のアシスタント講師を募集しています。
投稿者プロフィール

- 代表取締役
-
セイ・コンサルティング・グループ株式会社代表取締役。
岐阜県出身。
2000年創業、2004年会社設立。
IT企業向け人材育成研修歴業界歴20年以上。
すべての無駄を省いた費用対効果の高い「筋肉質」な研修を提供します!
この記事に間違い等ありましたらぜひお知らせください。
学生時代は趣味と実益を兼ねてリゾートバイトにいそしむ。長野県白馬村に始まり、志賀高原でのスキーインストラクター、沖縄石垣島、北海道トマム。高じてオーストラリアのゴールドコーストでツアーガイドなど。現在は野菜作りにはまっている。


