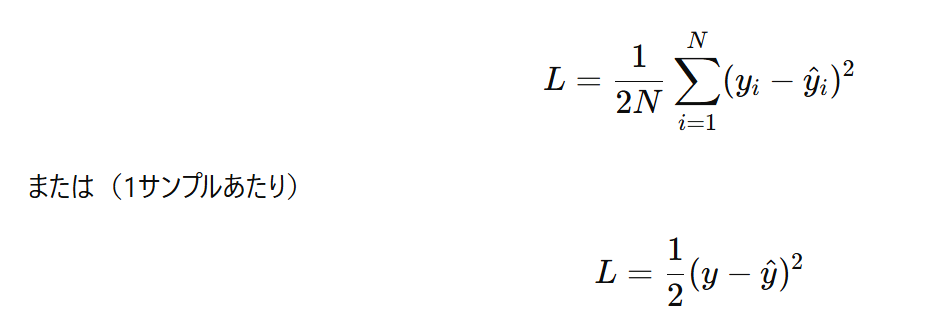【初心者向け】平均２乗誤差（MSE）とは？AIが「間違い」を測るしくみをわかりやすく解説

2026年1月27日 2026年1月27日山崎講師

山崎講師

こんにちは。ゆうせいです。

みなさんは、自分の予想が外れたとき、どのくらい外れたかをどうやって計算しますか。たとえば、テストの点数を80点だと予想していたのに、実際は60点だったとしましょう。悔しいですよね。

このとき、予想と結果のズレを数字で表したものを、機械学習の世界では誤差と呼びます。AIや機械学習モデルを作るとき、この誤差をできるだけ小さくすることが最大の目標になります。

きょうは、その誤差を測るためのもっとも有名な定規である平均２乗誤差についてお話しします。

なぜわざわざ２乗するのか。なぜ合計ではなく平均なのか。そして、なぜルートをつけて元の単位に戻さないのか。そんな素朴な疑問を、数式アレルギーの方でもわかるように紐解いていきましょう。

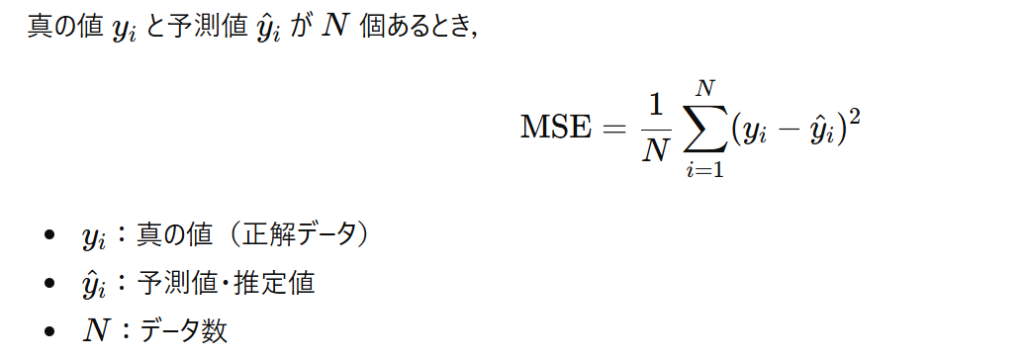
平均２乗誤差（MSE）ってなに？

まずは言葉の意味から整理しましょう。平均２乗誤差は、英語で Mean Squared Error といい、頭文字をとってMSEと呼ばれます。

一言でいうと、AIが予測を外した量の平均値です。

ここで想像してみてください。あなたは弓道の選手で、的の中心を狙って矢を放っています。中心からズレた距離が間違いの大きさですよね。このズレを全部集めて、ある特別な計算をして出した点数がMSEです。

この値が $0$ に近ければ近いほど、そのAIは優秀だといえます。

なぜ単純に引き算じゃダメなの？

もっとも単純な間違いの測り方は、実際の値と予測した値の引き算です。これを残差と呼びます。

たとえば、次のような予測をしたとしましょう。

データA：実際の値 $100$ 、予測 $80$

データB：実際の値 $100$ 、予測 $120$

データAのズレは $+20$ です。

データBのズレは $-20$ です。

もし、この単純なズレを合計してしまうとどうなるでしょうか。

$20 + (-20) = 0$

なんと、合計は $0$ になってしまいました。これでは、どちらも大きく外しているのに、全体としては完璧に予測できていることになってしまいます。プラスの失敗とマイナスの失敗が打ち消し合ってしまうのです。

これではAIの成績を正しく評価できませんね。そこで登場するのが２乗というアイデアです。

なぜ「２乗」するの？

マイナスの値をプラスに変えるには、同じ数を掛け合わせる、つまり２乗するのが手っ取り早い方法です。

先ほどの例で計算してみましょう。

データAのズレの２乗： $20 \times 20 = 400$

データBのズレの２乗： $-20 \times -20 = 400$

こうすれば、プラスの方向への失敗も、マイナスの方向への失敗も、等しく失敗としてカウントできます。これを足し合わせると $800$ になり、ちゃんとズレが存在することがわかりますね。

また、２乗にはもうひとつ大きなメリットがあります。それは、大きな失敗を厳しく罰することができるという点です。

ズレが $2$ のとき、２乗すると $4$ です。

しかし、ズレが $10$ になると、２乗すると $100$ になります。

失敗が５倍になっただけなのに、ペナルティは２５倍に膨れ上がりました。つまり、平均２乗誤差を使うことで、AIに対して「小さなミスは許してやるが、大きなミスだけは絶対にするなよ」と教え込むことができるのです。

なぜ「合計」ではなく「平均」をとるの？

２乗したズレを全部足したものを、専門用語で誤差２乗和（SSE）と言います。

では、なぜそこで止めずに、データの個数で割って平均を出すのでしょうか。

それは、データの数が多いテストと少ないテストを公平に比べるためです。

たとえば、10問のテストと100問のテストで、間違えた量の合計だけを比べたらどうなるでしょうか。当然、100問あるほうが合計のミスは大きくなりやすいですよね。これでは、問題数が多いだけで優秀ではないと判断されてしまいます。

データの個数 $n$ で割ることで、問題数が何問あろうとも、1問あたりの間違いの量はどのくらいかという同じ土俵で比べることができるようになります。だから、合計ではなく平均を使うのです。

なぜルート（平方根）に入れないの？

ここが一番の疑問ポイントかもしれません。

２乗してしまったのだから、最後にルート（ $\sqrt{}$ ）をつけて元の単位に戻してあげるのが親切だと思いませんか。実際、ルートをつけたものは２乗平均平方根誤差（RMSE）と呼ばれ、私たち人間が直感的に誤差を理解するときによく使われます。

しかし、AIを学習させるとき、つまり計算機の中では、あえてルートをつけないMSEのほうが好まれるのです。

理由は単純です。計算が楽だからです。

AIが学習するというのは、数学的には微積分という計算を使って、誤差が一番低くなる場所を探す作業です。このとき、ルートがついている数式を微分するのは、計算がとても複雑で面倒になります。

一方で、ただの２乗の式であれば、高校数学で習うような簡単な公式で微分ができます。

$x^2$ を微分すると $2x$ になる。

このシンプルさが、膨大な計算を繰り返すコンピュータにとっては非常にありがたいのです。計算スピードが上がり、効率よく学習を進めることができます。

平均２乗誤差（MSE）のメリットとデメリット

ここで一度、MSEの良い点と悪い点を整理しておきましょう。

メリット

大きな誤差を強調できるため、致命的なミスを減らす学習に向いている。

計算式がシンプルで、微分がしやすく、AIの学習計算がスムーズに進む。

多くの統計的な手法の基礎となっており、応用範囲が広い。

デメリット

単位が元のデータの２乗（例：メートルの２乗）になるため、人間が見ても直感的にどれくらいズレているかがわかりにくい。

例外的な値（外れ値）に敏感すぎて、たったひとつの極端なデータに全体の学習が引っ張られてしまうことがある。

まとめ

平均２乗誤差（MSE）について、イメージは掴めましたか。

単純に引き算しただけではプラスとマイナスが打ち消し合ってしまう。それを防ぐために２乗してすべてプラスにする。

データの数に関係なく評価するために、平均をとる。

そして、コンピュータが計算しやすいように、あえてルートはつけずにそのままにしておく。

これが、MSEがAI開発の現場で愛用されている理由です。

「間違いを２乗して平均する」という一見不思議な操作の裏には、こうした合理的な理由が隠されていたのですね。

もし、さらにこの分野を深く学びたいと思ったら、次は誤差逆伝播法というキーワードについて調べてみてください。今回学んだMSEが、実際にどのようにしてAIを賢くしていくのか、その核心に触れることができるはずです。

では、またお会いしましょう。

セイ・コンサルティング・グループでは新人エンジニア研修のアシスタント講師を募集しています。

投稿者プロフィール

山崎講師代表取締役

セイ・コンサルティング・グループ株式会社代表取締役。
岐阜県出身。
2000年創業、2004年会社設立。
IT企業向け人材育成研修歴業界歴20年以上。
すべての無駄を省いた費用対効果の高い「筋肉質」な研修を提供します！
この記事に間違い等ありましたらぜひお知らせください。

学生時代は趣味と実益を兼ねてリゾートバイトにいそしむ。長野県白馬村に始まり、志賀高原でのスキーインストラクター、沖縄石垣島、北海道トマム。高じてオーストラリアのゴールドコーストでツアーガイドなど。現在は野菜作りにはまっている。