【新人エンジニア向け｜階層的クラスタリングとは？考え方・仕組み・図解でやさしく理解】

こんにちは。ゆうせいです。

今回は、階層的クラスタリング（Hierarchical Clustering）について、統計や機械学習が初めての新人エンジニアにもわかるように、やさしく解説します！

名前からして「難しそう…」と思うかもしれませんが、実は発想はとてもシンプルなんです。この記事を読み終える頃には、「なんだ、木を育てるような話か」と思えるようになります。

---

階層的クラスタリングとは？

一言でいうと？

データ同士の「近さ」を元に、段階的にグループを作っていく方法です。

たとえば、友達のグループ分けを考えるとき、

• 「まずは似てる2人をペアにする」
• 「そのペアに近い別の人を追加する」
• 「だんだん大きなグループになる」

というように、下から上へグループが構築されるイメージです。

---

なぜ「階層的」なの？

クラスタリングには2種類ある

手法	特徴
階層的クラスタリング	グループ数を決めなくてもOK！
K-meansクラスタリング	あらかじめK（グループ数）を指定

階層的クラスタリングは、木のようにどんどん分岐・統合していく構造を作るため、「階層的」と呼ばれます。

この分岐の様子を「デンドログラム（dendrogram）」という図で表します。

---

アルゴリズムの2種類

階層的クラスタリングには2つのアプローチがあります。

手法名	意味	動き方
凝集型（agglomerative）	下から上へ	小さなクラスタから統合していく
分割型（divisive）	上から下へ	全体から分割していく

一般的によく使われるのは、凝集型です。この記事ではこちらを中心に説明します。

---

凝集型クラスタリングの流れ

ステップごとに見てみよう！

1. すべてのデータ点を1つずつのクラスタにする
2. 最も近いクラスタ同士を結合する
3. また最も近いクラスタを探して結合
4. 全てが1つになるまで繰り返す

図にすると、木が上に向かって育っていくイメージになります。

---

距離の定義が重要！

クラスタ同士の「近さ」をどう計算するかにはいくつかの方法があります。

方法	意味	特徴
単連結法（single linkage）	2つのクラスタの最短距離	細長いクラスタになりやすい
完全連結法（complete linkage）	最長距離	コンパクトなクラスタになる
平均連結法（average linkage）	全体の平均距離	バランス型

状況に応じて適切な方法を選ぶのがコツです。

---

デンドログラムを読み解こう

階層的クラスタリングでは、デンドログラムという図を使ってクラスタの統合の様子を表します。

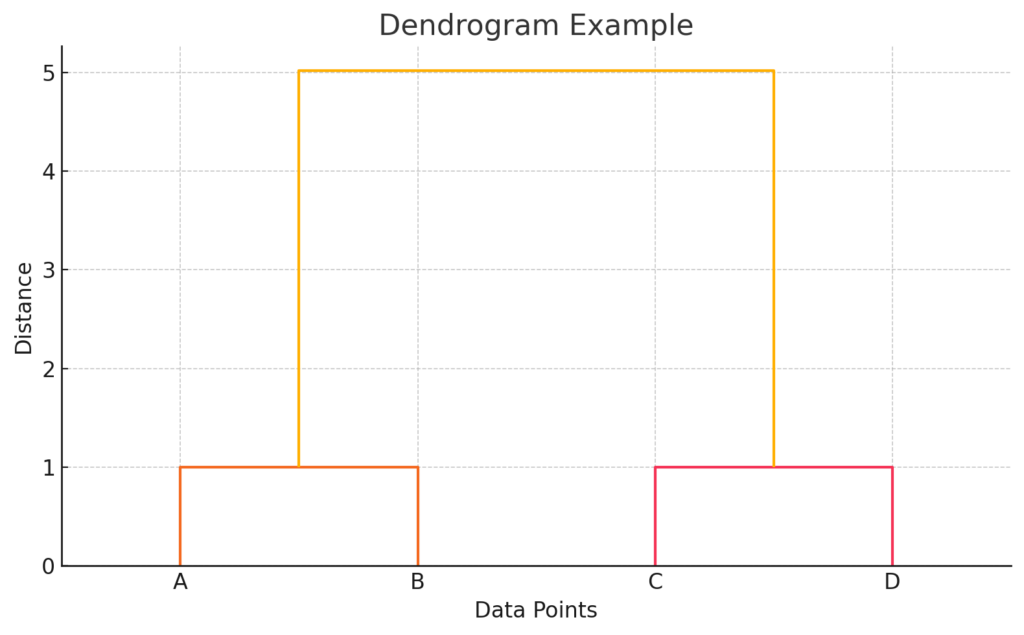
図の見方（重要ポイント）：

• A, B, C, D はデータ点（今回の例では4つの2次元点）
• 縦軸 は「クラスタ間の距離」（どれくらい似ているか）
• **下の方でつながっているほど、似ている（近い）」

たとえば：

• AとB が最初にクラスタになっています → 非常に近い
• CとD も比較的近いので次に結合
• 最後に「(AB)」と「(CD)」の2つの大きなクラスタが統合されます

このように、どこで線を横に引くか（どこで切るか）によってクラスタの数が変わるという特徴があります！

これが「階層的クラスタリング」の出力結果として、最もよく使われる図です。

---

木構造との違い

デンドログラムと木（ツリー構造）はどちらも階層構造を可視化する図ですが、目的と表現に違いがあります。

デンドログラムは主に階層的クラスタリングの結果を表すもので、クラスタ間の距離（類似度）を縦軸に持つことが特徴です。一方で、一般的な木構造（例えば二分木やディレクトリ構造）は、親子関係や順序、構造の階層を表しますが、ノード間の「距離」は示しません。

つまり、デンドログラムは「どれくらい近いか」まで示す木構造的な図であり、ただの木構造は構造の順序のみを表すという違いがあります。

---

階層的クラスタリングのメリット・デメリット

メリット	デメリット
グループ数を決めなくてよい	計算コストが高い（大規模データに不向き）
結果を図（デンドログラム）で視覚的に確認できる	一度の結合はやり直せない（貪欲法）
ノイズに強いこともある	次元が高いと効果が薄れることも

---

よくある活用場面

• ユーザー行動のグループ化
• 顧客セグメンテーション
• 遺伝子の系統解析
• テキストのクラスタリング

データの「関係性」や「構造」を知りたいときにとても役立ちます！

---

今後の学習の指針

階層的クラスタリングを理解したら、次は次の内容に進んでみましょう。

• クラスタ間の距離定義の違いと比較
• K-meansなど他のクラスタリングとの比較分析
• 次元削減（PCA）との組み合わせ
• 高次元データへの応用方法

また、scikit-learn や seaborn を使って、もっと実用的なデータでクラスタリングを試してみると、理解が一段と深まりますよ！

それでは、次の学習でまたお会いしましょう！

生成AI研修のおすすめメニュー

投稿者プロフィール

山崎講師代表取締役

セイ・コンサルティング・グループ株式会社代表取締役。
岐阜県出身。
2000年創業、2004年会社設立。
IT企業向け人材育成研修歴業界歴20年以上。
すべての無駄を省いた費用対効果の高い「筋肉質」な研修を提供します！
この記事に間違い等ありましたらぜひお知らせください。

最新の投稿

• 全ての社員2025年7月7日バッチ正規化の名前は何から来てるの？
• 全ての社員2025年7月7日SVMとカーネル法の「名前」に注目して、仕組みを理解しよう！
• 全ての社員2025年7月7日Lasso回帰とRidge回帰とは？新人エンジニアにやさしく解説！
• 全ての社員2025年7月7日【初心者向け】Q学習とSARSAとは？