AIが賢くなる秘密の鍵！初心者でもわかる最適化アルゴリズムの世界

2026年2月4日 2026年2月7日山崎講師

山崎講師

こんにちは。ゆうせいです。

みなさんは、AIがどうやって学習を進めているか想像したことはありますか？実はAIの学習とは、山頂からふもとの「正解」というゴールを目指して、険しい山道を下るような作業なのです。

この山を下るための戦略を、専門用語で「最適化アルゴリズム」と呼びます。どの道を選び、どれくらいのスピードで歩くのか。この戦略一つで、AIが天才になるかどうかが決まってしまうと言っても過言ではありません！

今回は、現代のAI開発には欠かせない5つの代表的な手法を、初心者の方にもわかりやすく解説しますね。

基本のキ！SGD（確率的勾配降下法）

まずは、すべての基本となるSGDから紹介しましょう。これは「Stochastic Gradient Descent」の略称で、日本語では「確率的勾配降下法」と訳されます。

Stochasticは「確率的」、Gradientは「勾配（傾き）」、Descentは「下ること」を意味します。

仕組みと特徴

SGDを一言で表すと「足元の傾斜だけで進む」という、非常にストレートな方法です。目隠しをして山に立たされ、足の裏で感じる地面の角度だけを頼りに、一番低い場所を探すと想像してください。

数式で表すと、以下のようになります。

新しい重み = 元の重み - 学習率 $\times$ 今の傾き（勾配）

重み更新の数式は次のようになります。

$W \leftarrow W - \eta \times \frac{\partial L}{\partial W}$

ここで、 $W$ は更新したい重み、 $\eta$ は学習率（歩幅）、 $\frac{\partial L}{\partial W}$ は勾配（坂道の傾き）を表します。

ここで登場する「学習率」とは、一歩の大きさを決める歩幅のことです。今の傾きが急であれば大きく、緩やかであれば小さく動きます。

メリットとデメリット

メリットは、計算が非常にシンプルで動作が軽い点にあります。余計なことを考えず、今の状況に集中するタイプですね。

しかし、足元の情報しか見ていないため、小さな穴ぼこや、なだらかな平地が続く場所に迷い込むと、そこがゴールだと思い込んで動けなくなってしまう弱点があります。

勢いをつけて駆け抜ける！Momentum（モーメンタム）

次に登場するのが、SGDに「勢い」を加えたMomentumです。

仕組みと特徴

Momentumとは、物理の言葉で「慣性」を意味します。重いボールが坂道を転がるとき、スピードに乗ると少々のデコボコは気にせず突き進みますよね？

数式では、速度という概念が登場します。

まず、速度に関する計算です。

新しい速度 ← 慣性係数 × 現在の速度 - 学習率 × 今の傾き（勾配）

次に、この速度を使って重みを更新します。

新しい重み ← 現在の重み + 新しい速度

数式で書くと以下のとおりです。

$v \leftarrow \alpha \times v - \eta \times \frac{\partial L}{\partial W}$

$W \leftarrow W + v$

$\alpha$ は前回の勢いをどれくらい残すか決める係数です。

このように、今の傾きだけでなく、これまでの進んできた勢いも計算に含めます。

メリットとデメリット

最大のメリットは、SGDが苦手としていた小さな窪みを、スピードに乗って突破できる点です。

ただ、勢いがつきすぎてしまい、本来止まるべきゴール地点を通り過ぎてしまうこともあります。まるでお調子者のランナーのようですね！

慎重派の歩幅調整！AdaGrad（アダグレード）

ここからは、歩幅を賢く変えていく手法を見ていきましょう。AdaGradは Adaptive Gradient Algorithm の略で、日本語では「適応的勾配アルゴリズム」と呼ばれます。

Adaptive（適応的）という言葉通り、状況に合わせて自分を変えるのが得意です。これまでの学習でたくさん動いた重みは「もう十分知っている」と判断して歩幅を小さくし、あまり動いていない重みは「もっと探検が必要だ」と考えて歩幅を大きく保ちます。

仕組みと特徴

AdaGradは、過去にどれくらい動いたかに応じて、自分自身の歩幅（学習率）を自動で調整します。

これまでの勾配のエネルギーを $h$ に溜めて、歩幅を調整します。

まず、これまでの経験を蓄積する計算です。

新しい勾配の蓄積＝現在の勾配の蓄積＋今の勾配 × 今の勾配

次に、その蓄積を使って、重みをどれくらい動かすか調整して更新します。

新しい重み＝現在の重み－学習率 × （ 1 ÷ 勾配の蓄積のルート） × 今の勾配

数式では以下のようになります。

$h \leftarrow h + \frac{\partial L}{\partial W} \times \frac{\partial L}{\partial W}$

$W \leftarrow W - \eta \times \frac{1}{\sqrt{h}} \times \frac{\partial L}{\partial W}$

何度も通って傾きが蓄積された道では、分母が大きくなるため、一歩の歩幅が小さくなります。

メリットとデメリット

初めて通る道は大胆に、よく知っている道は慎重に進むため、効率よく探索ができます。

一方で、学習が長く続くと蓄積された値がどんどん大きくなり、最終的には歩幅が極端に小さくなって、ゴールにたどり着く前に足が止まってしまうという致命的な弱点があります。

過去を適度に忘れる！RMSProp（アールエムエスプロップ）

AdaGradの「歩幅がなくなってしまう」という問題を解決したのが、このRMSPropです。Root Mean Square Propagation の略です。

仕組みと特徴

仕組みはAdaGradに似ていますが、大きな違いは「古い記憶を適度に忘れる」という点にあります。

まず、過去の勾配のエネルギー（蓄積量）を調整します。

新しい勾配のエネルギー＝減衰率 × これまでの勾配のエネルギー＋（1 －減衰率） × 現在の勾配の 2 乗

次に、このエネルギーを使って重みを更新します。

新しい重み＝現在の重み－学習率 × （1 ÷ 新しい勾配のエネルギーの平方根） × 現在の勾配

$\rho$ という減衰係数を使って、過去の記録をほどよくリセットします。

数式で書くと以下の通りです。

$h \leftarrow \rho \times h + (1 - \rho) \times \frac{\partial L}{\partial W} \times \frac{\partial L}{\partial W}$

$W \leftarrow W - \eta \times \frac{1}{\sqrt{h}} \times \frac{\partial L}{\partial W}$

ずっと昔の蓄積をいつまでも抱え込まず、直近の傾きを重視して歩幅を決めます。

メリットとデメリット

AdaGradのメリットを活かしつつ、途中で足が止まるリスクを回避しました。非常にバランスの取れた手法です。

最強のハイブリッド！Adam（アダム）

最後に紹介するのが、現在もっとも人気のあるAdamです。Adaptive Moment Estimation の略称で、名前からも分かる通り、これまで紹介したMomentum（勢い）とRMSProp（歩幅の調整）の良いとこ取りをした手法です。

仕組みと特徴

Adamは、いわば「Momentum」の勢いと、「RMSProp」の賢い歩幅調整をガッチャンコさせた最強のアルゴリズムです。

「勢い」と「歩幅の調整」という2つの情報を同時にアップデートしているのが特徴です。

まずは、「勢い」に関する更新です。

新しい勢いの記録 ← ベータ1 × 現在の勢いの記録 + （1 - ベータ1） × 現在の勾配

次に、「歩幅の調整（勾配の変動）」に関する更新です。

新しい勾配の変動記録 ← ベータ2 × 現在の勾配の変動記録 + （1 - ベータ2） × 現在の勾配 × 現在の勾配

（※この2つの記録を使って、最終的な重みの更新量を計算します）

勢いよく進みながら、状況に合わせて歩幅も変える。まさに非の打ち所がない現代の標準装備と言えます！

数式で書くと以下の通りです。

$m \leftarrow \beta_{1} \times m + (1 - \beta_{1}) \times \frac{\partial L}{\partial W}$

$v \leftarrow \beta_{2} \times v + (1 - \beta_{2}) \times \frac{\partial L}{\partial W} \times \frac{\partial L}{\partial W}$
（※実際にはここからバイアス補正を行って $W$ を更新します）

メリットとデメリット

ほとんどのケースにおいて、このAdamを選んでおけば間違いありません。それくらい優秀です。

弱点を挙げるとすれば、計算が少し複雑になるため、ほんの少しだけ処理に時間がかかることくらいでしょうか。

手法の比較まとめ

これまでの内容を表にまとめてみました。

手法名	由来のキーワード	特徴
SGD	確率的な降下	シンプルで高速だが、動きが不安定
Momentum	運動量・慣性	勢いをつけて、ジグザグを解消する
AdaGrad	適応的な歩幅	よく動く部分は慎重に、動かない部分は大胆に進む
RMSProp	二乗平均平方根	AdaGradの弱点を克服し、最後まで動き続ける
Adam	適応的な勢い推定	勢いと歩幅調整を組み合わせた最強の万能型

視覚的に確認できるPythonコード

各コードを実行すると、グラフが保存されるか画面に表示されます。ぜひ手元で動かしてみてくださいね。

準備：実験する「山」を定義する

まずは、私たちが下る山（関数）を決めましょう。

ここでは、 $y = x \times x$ という、きれいな谷底（ $x = 0$ ）を持つ放物線を想定します。この谷底を見つけるのがプログラムのゴールです。

今の場所（ $x$ ）における傾きは、 $2 \times x$ で求められます。

1. SGD：コツコツ一歩ずつ進む

まずは基本のSGDです。坂道の角度に合わせて一定のルールで下りていきます。

import matplotlib.pyplot as plt

# 設定
x = 10.0
lr = 0.1
x_history = [x]

# 学習
for i in range(20):
    grad = 2 * x
    x = x - lr * grad
    x_history.append(x)

# 可視化
plt.plot(x_history, 'o-', label='SGD')
plt.title('SGD Optimization')
plt.xlabel('Steps')
plt.ylabel('x value')
plt.legend()
plt.show()

実行結果

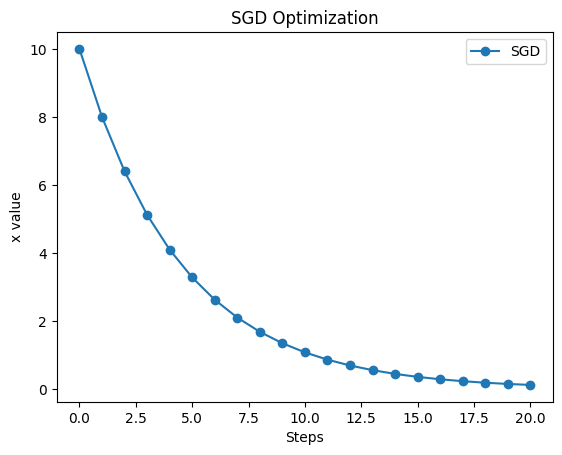
2. Momentum：加速して一気に下る

過去の勢いを利用するため、最初はゆっくり、後半は加速していく様子に注目してください！

import matplotlib.pyplot as plt

# 設定
x = 10.0
lr = 0.05
v = 0
gamma = 0.9
x_history = [x]

# 学習
for i in range(20):
    grad = 2 * x
    v = gamma * v - lr * grad
    x = x + v
    x_history.append(x)

# 可視化
plt.plot(x_history, 'o-', color='orange', label='Momentum')
plt.title('Momentum Optimization')
plt.xlabel('Steps')
plt.ylabel('x value')
plt.legend()
plt.show()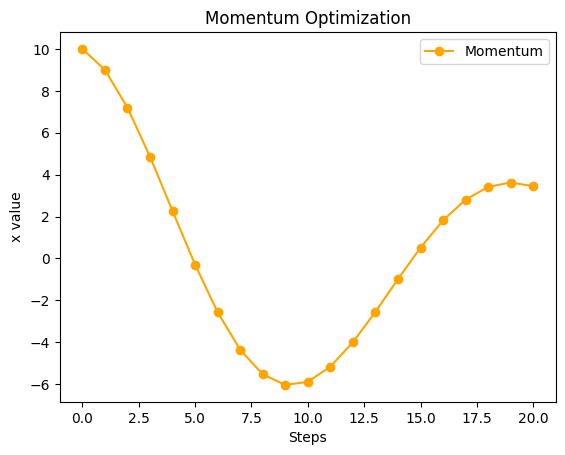

勢いがつきすぎて正解(x = 0)を飛び越えてしまっています。

3. AdaGrad：学習が進むほど慎重に

最初は大きく動きますが、次第に歩幅が小さくなっていくのがグラフの傾きからわかります。

import matplotlib.pyplot as plt
import numpy as np

# 設定
x = 10.0
lr = 1.5
h = 0
x_history = [x]

# 学習
for i in range(20):
    grad = 2 * x
    h = h + grad * grad
    x = x - (lr / (np.sqrt(h) + 1e-7)) * grad
    x_history.append(x)

# 可視化
plt.plot(x_history, 'o-', color='green', label='AdaGrad')
plt.title('AdaGrad Optimization')
plt.xlabel('Steps')
plt.ylabel('x value')
plt.legend()
plt.show()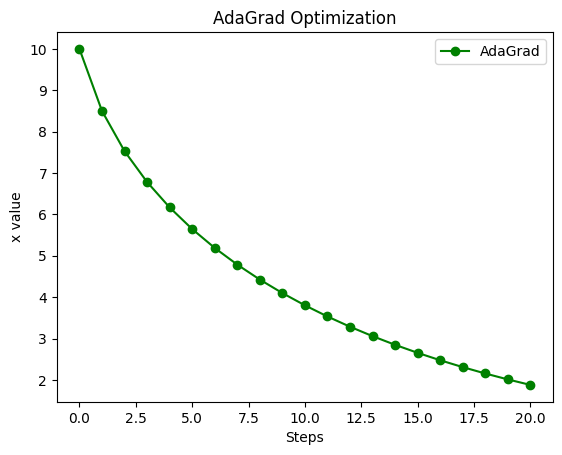

4. RMSProp：効率よく、止まらずに進む

AdaGradのように極端に歩幅が小さくなりすぎず、スムーズにゴールへ向かいます。

import matplotlib.pyplot as plt
import numpy as np

# 設定
x = 10.0
lr = 0.6
h = 0
rho = 0.9
x_history = [x]

# 学習
for i in range(20):
    grad = 2 * x
    h = rho * h + (1 - rho) * grad * grad
    x = x - (lr / (np.sqrt(h) + 1e-7)) * grad
    x_history.append(x)

# 可視化
plt.plot(x_history, 'o-', color='red', label='RMSProp')
plt.title('RMSProp Optimization')
plt.xlabel('Steps')
plt.ylabel('x value')
plt.legend()
plt.show()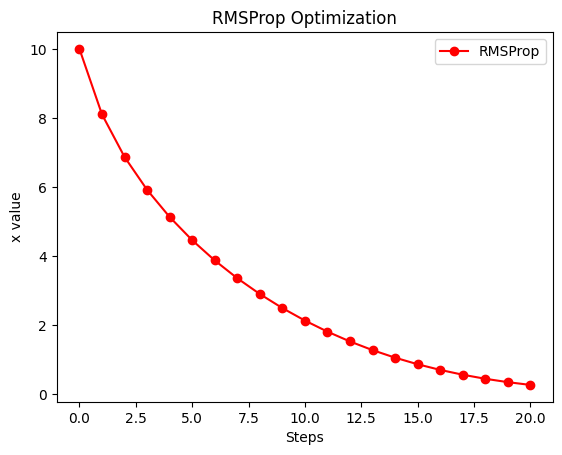

5. Adam：素早く正確にゴールへ

「勢い」と「歩幅調整」の良いとこ取りをしているので、非常に効率的なカーブを描きます！

import matplotlib.pyplot as plt
import numpy as np

# 設定
x = 10.0
lr = 0.6
m = 0
v = 0
beta1 = 0.9
beta2 = 0.999
x_history = [x]

# 学習
for i in range(20):
    grad = 2 * x
    m = beta1 * m + (1 - beta1) * grad
    v = beta2 * v + (1 - beta2) * (grad * grad)
    
    m_hat = m / (1 - beta1**(i+1))
    v_hat = v / (1 - beta2**(i+1))
    
    x = x - lr * m_hat / (np.sqrt(v_hat) + 1e-7)
    x_history.append(x)

# 可視化
plt.plot(x_history, 'o-', color='purple', label='Adam')
plt.title('Adam Optimization')
plt.xlabel('Steps')
plt.ylabel('x value')
plt.legend()
plt.show()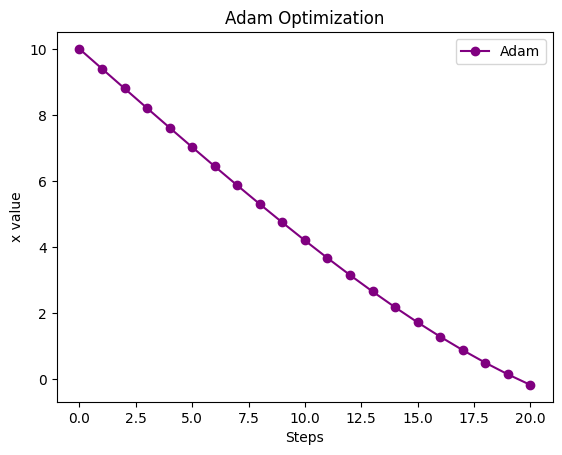

さいごに

5つのグラフを見比べてみて、何か気づいたことはありましたか？

同じゴール（ $x = 0$ ）を目指していても、そのたどり着き方はアルゴリズムによって千差万別です。

学習率（ $lr$ ）の数字を少し変えるだけで、グラフの形が劇的に変わるのも面白いポイントですよ！

次は、これらのアルゴリズムを使って、実際のデータから「予測」を行う本格的な機械学習に挑戦してみませんか？

セイ・コンサルティング・グループでは新人エンジニア研修のアシスタント講師を募集しています。

投稿者プロフィール

山崎講師代表取締役

セイ・コンサルティング・グループ株式会社代表取締役。
岐阜県出身。
2000年創業、2004年会社設立。
IT企業向け人材育成研修歴業界歴20年以上。
すべての無駄を省いた費用対効果の高い「筋肉質」な研修を提供します！
この記事に間違い等ありましたらぜひお知らせください。

学生時代は趣味と実益を兼ねてリゾートバイトにいそしむ。長野県白馬村に始まり、志賀高原でのスキーインストラクター、沖縄石垣島、北海道トマム。高じてオーストラリアのゴールドコーストでツアーガイドなど。現在は野菜作りにはまっている。

AIが賢くなる秘密の鍵！初心者でもわかる最適化アルゴリズムの世界

基本のキ！SGD（確率的勾配降下法）

仕組みと特徴

メリットとデメリット

勢いをつけて駆け抜ける！Momentum（モーメンタム）

仕組みと特徴

メリットとデメリット

慎重派の歩幅調整！AdaGrad（アダグレード）

仕組みと特徴

メリットとデメリット

過去を適度に忘れる！RMSProp（アールエムエスプロップ）

仕組みと特徴

メリットとデメリット

最強のハイブリッド！Adam（アダム）

仕組みと特徴

メリットとデメリット

手法の比較まとめ

視覚的に確認できるPythonコード

準備：実験する「山」を定義する

1. SGD：コツコツ一歩ずつ進む

2. Momentum：加速して一気に下る

3. AdaGrad：学習が進むほど慎重に

4. RMSProp：効率よく、止まらずに進む

5. Adam：素早く正確にゴールへ

さいごに

セイ・コンサルティング・グループでは新人エンジニア研修のアシスタント講師を募集しています。

投稿者プロフィール

最新の投稿

スマホでAIがサクサク動く秘密！MobileNetの「分業」の魔法を解説

初心者でもわかる！計算グラフで紐解く逆伝播の仕組みと計算のルール