AIの学習を加速させる！強化学習の核心「ベルマン方程式」を世界一わかりやすく解説
山崎講師こんにちは。ゆうせいです。
あなたは、何かを決断するときに「これをしたら将来どうなるかな？」と考えたことはありませんか。
例えば、今このブログを読むという選択が、将来のあなたのスキルをどれだけ高めるか、そんな風に未来の価値を計算することを、数学の世界ではかっこよく表現できるのです。
今日は、人工知能（AI）が賢くなるための魔法の数式、ベルマン方程式について一緒に学んでいきましょう！
ベルマン方程式とは未来を見通す計算式
強化学習という分野において、この方程式は避けて通れない非常に重要な存在です。
一言で言えば、現在の価値は、今もらえる報酬と、将来もらえる価値の合計である、と定義する式のことですね。
でも、数式と聞くと少し身構えてしまいませんか。
大丈夫ですよ。
まずは、私たちが日常生活で無意識に行っている「価値判断」を言葉に置き換えるところから始めてみましょう。
専門用語の解説：状態と行動、そして報酬
ベルマン方程式を理解するために、まずは3つの重要な言葉をマスターしましょう。
- 状態（State）：今、自分が置かれている状況のことです。RPGゲームで例えるなら、勇者が洞窟の入り口に立っているのか、それとも魔王の目の前にいるのか、という現在地を指します。
- 行動（Action）：その状態で取るアクションのことです。右に進む、攻撃する、あるいは逃げるといった選択肢ですね。
- 報酬（Reward）：行動した結果、得られるご褒美です。宝箱を見つけたらプラスの報酬、罠にかかったらマイナスの報酬といった具合に数値で表されます。
価値を再帰的に表現するとはどういうことか
ベルマン方程式の最大の特徴は、価値を再帰的に表現している点にあります。
再帰的という言葉は、少し難しい響きがしますよね。
これは、自分自身の定義の中に、自分自身が含まれている状態を指します。
マトリョーシカ人形を想像してください。
大きな人形を開けると、中から少し小さな同じ形の人形が出てきます。
ベルマン方程式も同じで、今の価値を計算しようとすると、その中には次の瞬間の価値が含まれているのです。
なぜ再帰的なのか
私たちが「今の場所の価値」を決めるとき、その場所自体に魅力がある場合もありますが、多くの場合は「そこから次にどこへ行けるか」で価値が決まりませんか。
例えば、駅から徒歩1分の物件が高いのは、駅そのものに住みたいからではなく、そこからどこへでも行けるという未来の価値が含まれているからです。
これを数式っぽく表現すると、以下のようになります。
今の価値 
このように、今の価値を説明するために未来の価値を使う手法を、再帰的と呼びます。
期待値という考え方で不確実性に備える
さて、未来のことは誰にも分かりません。
サイコロを振って1が出るかもしれないし、6が出るかもしれない。
AIの世界でも、ある行動をとったときに必ず特定の状態になるとは限りません。
そこで登場するのが期待値という考え方です。
期待値とは、起こりうるすべての結果を、その起こりやすさ（確率）で重み付けして平均した値のことです。
降水確率が 
ベルマン方程式は、この期待値を使って、不確実な未来の価値を賢く見積もるのです。
ベルマン方程式のメリットとデメリット
この方程式を使うことで、AIはどのように進化するのでしょうか。
メリット
- 複雑な未来をシンプルに計算できる何手先も続く未来の価値を、一歩先の価値との関係性だけで表現できるため、計算の効率が劇的に上がります。
- 迷いなく最適な行動を選べるすべての状態の価値がわかれば、AIは常に価値が最も高い方向へ進むだけで、ゴールにたどり着くことができます。
デメリット
- 計算量が膨大になることがある囲碁や将棋のように、状態の数が天文学的な数字になる場合、すべてを正確に計算するのは現代のコンピュータでも困難です。
- 未来の予測が外れると弱いあくまで予測に基づいているため、環境が急激に変わると、計算していた価値が役に立たなくなることがあります。
ベルマン方程式の構造
それでは、数式の形を見てみましょう。
日本語の部分と数式の部分に注目してください。
状態 
![V(s') ]](https://s0.wp.com/latex.php?latex=V%28s%27%29+%5D&bg=ffffff&fg=000&s=0&c=20201002)
ここで登場した 
明日もらえる 
遠い未来の価値を少しだけ割り引いて計算するための、魔法の係数だと覚えておいてください。
それでは、より専門的な形式で、ベルマン方程式を分解してみましょう。
数式と聞くと、まるで暗号のように見えるかもしれませんね。
でも、一つ一つの記号には「今の報酬」や「未来の期待」といった、私たちの日常に馴染みのある意味が込められています。
この数式の美しさは、無限に続く未来の価値を、たった一行の「現在の関係式」に凝縮したところにあります！
ベルマン方程式の数学的表現
強化学習で最も基本となる、状態価値関数
ある状態 
![r + \gamma \times V(s') ]](https://s0.wp.com/latex.php?latex=r+%2B+%5Cgamma+%5Ctimes+V%28s%27%29+%5D&bg=ffffff&fg=000&s=0&c=20201002)
この式が、なぜ世界を変えるほど重要なのか、パーツごとに深掘りしていきましょう。
1. 左辺： （現在の価値）
これは、今あなたがいる「状態
高校の数学で習う関数と同じで、場所に数字を割り当てるイメージですね。
2. 右辺の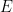 
（期待値）
ここが知的なポイントです！
未来は不確実ですよね？
サイコロを振って次にどこへ行くか決まるような状況でも、起こりうるすべてのパターンの平均値を計算するのが、この
3. 右辺の 
（即時報酬）
その場所で「今すぐ」もらえるご褒美です。
ゲームで言えば、落ちているコインを拾った瞬間のプラス評価だと思ってください。
4. 右辺の 
（割引かれた将来価値）
そして 
「明日の
これにより、遠すぎる未来の不確実な報酬に惑わされず、現実的な判断ができるようになります。
数式を言葉で読み解く
この式を日本語で音読するなら、こんな感じになります。
「今の場所の価値は、今すぐもらえる報酬と、次に行く場所の価値をちょっと割り引いたものの合計（の平均）である！」
いかがですか？
こうして見ると、私たちが投資をしたり、勉強をしたりするときの思考プロセスそのものだと思いませんか。
AIはこの数式を何万回、何億回と計算し直すことで、「どの状態にいるのが一番得か」を学習していくのです。
まとめと今後の学習指針
ベルマン方程式は、一見すると難解な数式に見えますが、その本質は「今と未来を繋ぐ架け橋」です。
AIが試行錯誤しながら、どの道を進むのが一番幸せかを計算するための、非常に人間味のある理論だと思いませんか。
この記事で、強化学習の入り口に立つことができましたね！
次のステップとして、以下の学習に挑戦してみてください。
- Q学習（Q-Learning）を調べてみるベルマン方程式を実際に応用して、AIが学習していく具体的な仕組みを学べます。
- Pythonで簡単な迷路解きプログラムを動かしてみる数式が実際に動く様子を見ると、理解がさらに深まりますよ。
もし、この数式があなたの人生の価値を最大化するヒントになったなら、これほど嬉しいことはありません。
セイ・コンサルティング・グループでは新人エンジニア研修のアシスタント講師を募集しています。
投稿者プロフィール
