AIを育てる魔法の計算！なぜ「全微分」ではなく「偏微分」が重要なのか？

2026年1月27日 2026年1月27日山崎講師

山崎講師

こんにちは。ゆうせいです。

AI（人工知能）が自ら学習して賢くなっていく姿は、まるで魔法のように見えますよね。その魔法の杖ともいえる技術が「誤差逆伝播法（バックプロパゲーション）」です。

でも、この技術を学ぼうとすると必ずぶつかる壁があります。「なぜ微分を使うのか？」そして「なぜ全微分ではなく偏微分なのか？」という疑問です。

今日は、研修講師として皆さんのモヤモヤをスッキリ解決していきます。一緒にAIの頭の中を覗いてみましょう！

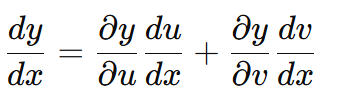
AIの「反省」を支える微分の力

そもそも、AIが学習するというのはどういう状態を指すのでしょうか。

簡単に言えば、AIが出した「答え」と「正解」のズレを最小にすることです。このズレのことを専門用語で「損失関数」と呼びます。

この損失関数の値をどんどん小さくしていく作業は、深い霧の中で山の頂上からふもとを目指して下っていくようなものです。足元の傾斜を調べて、どちらに一歩踏み出せばより低くなるかを確認しますよね。

この「足元の傾斜」を数学的に求める道具こそが、微分なのです！

偏微分とは「特定のネジだけを回す」こと

ここで、今回のメインテーマである「偏微分」が登場します。

AIの中には、膨大な数の「重み」という調節ネジが存在します。例えば、1つのAIの中に数百万個、数億個のネジがあると想像してください。

偏微分とは、他のネジをすべて固定したまま、たった1つのネジだけを少し回したときに、全体のズレがどう変化するかを調べる手法です。

高校生の皆さんに例えるなら、テストの点数を上げるために「英語の勉強時間だけ」を増やしたとき、合計点がどう変わるかを計算するようなものです。数学や国語の勉強時間は一切変えません。

この「特定の要素にだけ注目する」という考え方が、偏微分の本質です。

なぜ全微分ではダメなのか？

一方で「全微分」という言葉もあります。これは、すべてのネジを同時に、少しずつ動かしたときに全体がどう変わるかを見る手法です。

一見すると、全微分の方が効率的に思えるかもしれません。しかし、AIの学習においては致命的な問題があります。

1. 犯人探しができない

AIの学習で大切なのは、ズレを生んでいる「戦犯」のネジを見つけ出し、それを修正することです。

全微分はすべての変数をまとめて扱ってしまうため、どのネジをどれくらい回せば最適なのかという、個別の修正指示が出せません。全員で連帯責任を取らされるクラスのようなもので、誰がサボっているのか分からないのです。

偏微分を使えば、「この3番目のネジが原因でズレが大きくなっているから、左に $\times$ 0.1 だけ回そう」という具体的な改善案が作れます。

2. 計算量が爆発する

全微分を厳密に扱おうとすると、すべての変数の相関関係を網羅しなければなりません。

現代のAIが持つ変数の数は天文学的です。それらすべてを一度に計算しようとすれば、スーパーコンピュータでもパンクしてしまいます。

偏微分なら、1つひとつのネジに対して独立して計算を進められるため、効率よく「誤差」を後ろから前へと伝言ゲームのように戻していく（逆伝播させる）ことが可能なのです。

偏微分を活用するメリットとデメリット

ここで、偏微分を誤差逆伝播法に使う際の特徴を整理しておきましょう。

項目	内容
メリット	各パラメーターの貢献度が明確になり、ピンポイントで修正できる
メリット	複雑な多変数関数でも、鎖のルール（連鎖律）を使って計算を簡略化できる
デメリット	あくまで「その地点での傾き」しか分からないため、局所的な正解（局所解）にハマることがある

あなたは、霧の中で一歩ずつ進むときに、右足の向きだけを変えて様子を見るのと、体全体をいきなり投げ出すのと、どちらが安全だと思いますか？

慎重に、かつ確実に下るためには、やはり偏微分による「個別の確認」が欠かせないのです。

誤差逆伝播法の計算イメージ

実際の計算では、以下のようなステップで進みます。

まず、出力された誤差 $E$ があります。これを特定の重み $w$ で偏微分します。

$\frac{\partial E}{\partial w}$

この記号は「 $w$ 以外の変数は定数だと思って、 $E$ を微分せよ」という命令です。

これにより、その重みを増やせば誤差が増えるのか、それとも減るのかという方向性がはっきりします。方向がわかれば、あとはその逆側に重みを更新するだけです。

更新式は以下のようになります。

新しい重み = 現在の重み $-$ 学習率 $\times$ $\frac{\partial E}{\partial w}$

シンプルだと思いませんか？この積み重ねが、自動運転や翻訳AIといった驚異的な技術を支えているのです。

これからの学習の指針

偏微分の役割がイメージできたでしょうか。数学の教科書の中だけの存在だった微分が、実は最新テクノロジーの心臓部を動かしているというのは、ワクワクする発見ですよね。

もしこの記事を読んで興味が湧いたら、次は以下のステップに進んでみてください。

合成関数の微分（連鎖律）を復習して、微分の伝言ゲームの仕組みを知る。
行列の掛け算を学び、大量の偏微分をまとめて処理する方法を理解する。
実際にPythonなどのプログラミング言語を使って、簡単なニューラルネットワークを動かしてみる。

数式の裏側にある「意味」がわかれば、AI学習はもっと楽しくなります。一歩ずつ、AIという大きな山のふもとを目指して進んでいきましょう！

次は、実際にこの偏微分を使ってどうやって「連鎖律」を適用していくのか、具体的な計算手順を一緒に見てみませんか？

セイ・コンサルティング・グループでは新人エンジニア研修のアシスタント講師を募集しています。

投稿者プロフィール

山崎講師代表取締役

セイ・コンサルティング・グループ株式会社代表取締役。
岐阜県出身。
2000年創業、2004年会社設立。
IT企業向け人材育成研修歴業界歴20年以上。
すべての無駄を省いた費用対効果の高い「筋肉質」な研修を提供します！
この記事に間違い等ありましたらぜひお知らせください。

学生時代は趣味と実益を兼ねてリゾートバイトにいそしむ。長野県白馬村に始まり、志賀高原でのスキーインストラクター、沖縄石垣島、北海道トマム。高じてオーストラリアのゴールドコーストでツアーガイドなど。現在は野菜作りにはまっている。