以下のプログラムを作成しなさい。

なお、コードテンプレートをできるだけ使用すること。

0.毎日１％の成長を続けると１年後には

新入社員のあなたは毎日１％の成長を続けたいと心に誓っています。

ふと気になって１年後の成長度合いを数値で確認することを思い立ちました。

以下のプログラムを完成させなさい。（小数点は丸めなくてOK）

package chap05;

public class Grow {

    public static void main(String[] args) {
        double growthRate = 1.01;
        double originalAbility = 1.0;
        final int DAYS_OF_YEAR = 365;

//        ここにfor文を書く

        System.out.println(originalAbility);
    }
}

1.継続条件式

0から100までの整数値を表示するプログラムを作成しなさい。

ただし、for文を使うこと。出力の最後は改行して終わるようにすること。

（出力例）

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100

2.初期化文

100から0までの整数値を表示するプログラムを作成しなさい。

ただし、for文を使うこと。出力の最後は改行して終わるようにすること。

（出力例）

100 99 98 97 96 95 94 93 92 91 90 89 88 87 86 85 84 83 82 81 80 79 78 77 76 75 74 73 72 71 70 69 68 67 66 65 64 63 62 61 60 59 58 57 56 55 54 53 52 51 50 49 48 47 46 45 44 43 42 41 40 39 38 37 36 35 34 33 32 31 30 29 28 27 26 25 24 23 22 21 20 19 18 17 16 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0

3.更新文

50から100までに含まれる偶数を表示するプログラムを作成しなさい。

ただし、for文を使うこと。出力の最後は改行して終わるようにすること。

（出力例）

50 52 54 56 58 60 62 64 66 68 70 72 74 76 78 80 82 84 86 88 90 92 94 96 98 100

4.合計の計算

1から100までに含まれる整数を全て合計するプログラムを作成しなさい。

ただし、for文を使うこと。

（出力例）

合計は5050です。

5.計算過程の表示

上記４のプログラムを計算過程を表示するように変更しなさい。

ただし、for文を使うこと。

（出力例）

1を足します。
現在の合計は1です。
2を足します。
現在の合計は3です。
3を足します。
現在の合計は6です。

（中略）

100を足します。
現在の合計は5050です。
合計は5050でした。

6.While文

上記１～５のプログラムをWhile文を使って書き換えなさい。

全てを一つのmainメソッドの中に作成してかまわない。

7.for文のネスト

System.out.print("*");

で１つのアスタリスクが表示できる。

このとき、次のような模様を出力するプログラムを2重のfor文で作りなさい。（printlnとprintの使い分けに注意）

（出力例）

**********
**********
**********
**********
**********

8.継続条件式を変化させる

次のような模様を出力するプログラムを2重のfor文で作りなさい

（出力例）

*
**
***
****
*****

9.インクリメントとデクリメント

次のような模様を出力するプログラムを2重のfor文で作りなさい

（出力例）

*****
****
***
**
*

10.HogeHuga問題

HogeHuga問題を解きなさい。

HogeHuga問題とは、1から99まで順番に数を表示するプログラムです。

ただし、その数が3で割り切れるなら“Hoge”、5で割り切れるなら“Huga”、両方で割り切れるなら“HogeHuga”と表示します。

（出力例）

1 2 Hoge 4 Huga Hoge 7 8 Hoge Huga 11 Hoge 13 14 HogeHuga 16 17 Hoge 19 Huga Hoge 22 23 Hoge Huga 26 Hoge 28 29 HogeHuga 31 32 Hoge 34 Huga Hoge 37 38 Hoge Huga 41 Hoge 43 44 HogeHuga 46 47 Hoge 49 Huga Hoge 52 53 Hoge Huga 56 Hoge 58 59 HogeHuga 61 62 Hoge 64 Huga Hoge 67 68 Hoge Huga 71 Hoge 73 74 HogeHuga 76 77 Hoge 79 Huga Hoge 82 83 Hoge Huga 86 Hoge 88 89 HogeHuga 91 92 Hoge 94 Huga Hoge 97 98 Hoge

11.コラッツの予想

コラッツの予想（のほんの一端）を解きなさい。

コラッツの予想とは、任意の正の整数numに対して
(1)　numが奇数ならば3倍して１を加える。
(2)　numが偶数ならば2で割る。
という操作を繰り返して，１になったら終了とするという処理があった時、
どんな正の整数から始めても上記の操作を繰り返せば１になる、というものです。

1930年代にコラッツが予想した数学界の未解決問題の一つです。

つまり、証明はまだ誰もなしえていません。

2021年7月7日にはこの問題に1億2,000万円の懸賞金が掛けられました。

（出力例：num=26の場合）

13 40 20 10 5 16 8 4 2 1

（出力例：num=27の場合）

82 41 124 62 31 94 47 142 71 214 107 322 161 484 242 121 364 182 91 274 137 412 206 103 310 155 466 233 700 350 175 526 263 790 395 1186 593 1780 890 445 1336 668 334 167 502 251 754 377 1132 566 283 850 425 1276 638 319 958 479 1438 719 2158 1079 3238 1619 4858 2429 7288 3644 1822 911 2734 1367 4102 2051 6154 3077 9232 4616 2308 1154 577 1732 866 433 1300 650 325 976 488 244 122 61 184 92 46 23 70 35 106 53 160 80 40 20 10 5 16 8 4 2 1

上記の通り、１違うだけでも全く予想のつかないアウトプットになります。

コラッツ数列のグラフ化へのリンク

本のご紹介

コラッツの予想がテーマになっている青春小説です。

「永遠についての証明」

12.紙を折ることによって月に到達できるか

紙を何度折ることによって月に到達できるかを計算するプログラムを作りなさい

紙の厚さは0.1㎜とする。

月までの距離は.平均で約38万キロとする。

ヒント：厚さをミリメートルからキロメートルへ単位変換する。

（出力例）

0.1㎜の紙を42回折ることで月に到達できます。
その時の紙の厚さは439804.6511104キロメートルです。

なお、この答えの数は大変神秘的な数として有名です。

13.IPv4で表現できるIPアドレス

IPv4で表現できるIPアドレスの理論上の数を求めなさい。

※IPv4は32ビットである。よって、2の32乗を計算することで求めなさい。
※累乗(べき乗)の計算をするMathクラスのpowメソッドは使わないこと。

ヒント：桁あふれ（オーバーフロー）に注意すること

（出力例）

4294967296

オーバーフローにはくれぐれも注意しましょう。過去にはこんな事件もありました。

14.モンテカルロ法による円周率計算

モンテカルロ法を使い円周率を計算しなさい。

なお、円周率とは円の直径に対する円周の長さの比率のことです。

(1)　モンテカルロ法の名前の由来を隣の人に教えてあげなさい。

(2)　プログラムで実装し、java.lang.Math.PI(3.141592653589793)にできるだけ近づけなさい

考え方：
　①半径１の円を考えます。
　②その円に外接する正方形（一辺は２）を考えます。
　③円の中心から右上の４分の１の円と正方形を取り出して考えます。
　④0～1のランダムな乱数を２つ作り、それぞれをx軸,y軸の座標値として点を打ちます。
　⑤円の中心と点（x,y）を結んだ直角三角形を考え、３平方の定理により斜辺を求めます。
　⑥もしも、斜辺の長さが１以下なら円の中に点が打たれたということです。
　⑦上記④～⑥の試行を一定回数繰り返し、全試行回数中、円の中に点が打たれた確率を求めます。
　⑧⑦で求めた確率を４倍すると求める円周率（の近似値）になります。

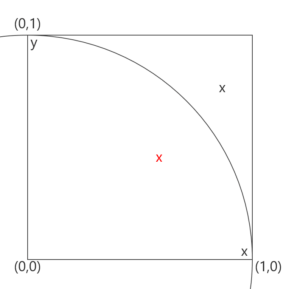
簡単な説明
　円の面積 ＝ 円周率 × 半径 × 半径
　４分の１の円の面積 ＝ 円周率 × (半径 × 半径) ÷ ４
　４分の１の正方形の面積 ＝ (半径 × 半径)
　４分の１の円の面積 ＝ 円周率 × (４分の１の正方形の面積) ÷ ４
　円周率 ＝ （４分の１の円の面積）÷ （４分の１の正方形の面積） × 4

ちなみに、以下のサイトでは円周率から任意の数値列の検索ができます｡
あなたの誕生日や電話番号などの数値があるかどうか確かめてみましょう。
http://www.subidiom.com/pi/
円周率にはこの世のすべての情報が含まれているという説があります。
あなたはどう思いますか?

延々と円周率を計算し続けるWebアプリケーションへのリンク

もう一つのモンテカルロ法の例「ビュフォンの針の実験」へのリンク

15.オリジナル問題作成

将来の後輩のために良い問題が出来たら教えてください。

以上。

JavaSEの問題集トップページに戻る