Lasso回帰とRidge回帰とは？新人エンジニアにやさしく解説！
山崎講師
こんにちは。ゆうせいです。
今回は、機械学習の中でもとても大切な「Lasso（ラッソ）回帰」と「Ridge（リッジ）回帰」について、新人エンジニアの方でも理解しやすいようにやさしく解説します。
線形回帰とは？
LassoやRidgeは、線形回帰（Linear Regression） をベースにした回帰手法です。
たとえば「部屋の広さ」や「駅までの距離」などの情報から家賃を予測する、というような場面で使います。
モデル式は以下の通りです：
特徴量とその重みの線形結合にバイアス bb を加えて、目的変数 y^\hat{y} を予測します。
過学習とは？なぜ正則化が必要？
実際のデータでは、特徴量が多くなりがちです。特徴量が増えるとモデルは柔軟になりすぎ、訓練データにはよく当てはまるが、新しいデータに弱い（過学習）という状態になります。
正則化（Regularization）とは？
モデルの複雑さに「罰則（ペナルティ）」を加えることで、シンプルに保ち、汎化性能を上げる手法が正則化です。
主な2種類がこちら：
| 手法 | 正則化の種類 | 特徴 |
|---|---|---|
| Ridge回帰 | L2正則化 | 重みをなだらかに縮小 |
| Lasso回帰 | L1正則化 | 一部の重みをゼロにする（選択） |
Ridge回帰とは？
Ridge回帰は、重みの二乗和にペナルティを課します。
- λ\lambda：正則化の強さ（大きいほど強く制限）
- 全ての重みをなめらかに小さくして、過学習を防ぎます
Lasso回帰とは？
Lasso回帰では、重みの絶対値の和をペナルティとして加えます。
- 不要な重みはゼロになり、特徴量の自動選択が可能です
- 高次元データやスパースな特徴に効果的です
名前の由来を知ろう
Lasso（ラッソ）
- 「投げ縄（lasso）」が語源
- データから重要な特徴量だけを「縄で捕まえる」ようなイメージ
- 正式名：Least Absolute Shrinkage and Selection Operator
Ridge（リッジ）
- 「尾根・稜線（ridge）」が語源
- 解の空間が連続・滑らかになりやすく、その形が尾根のように見える
| 名前 | 由来のイメージ | 特徴 |
|---|---|---|
| Lasso | 投げ縄（選び取る） | 特徴量選択・スパースモデリング |
| Ridge | 尾根（なだらかに縮める） | 全体をなめらかに抑える |
- 点線：Ridge（円形）
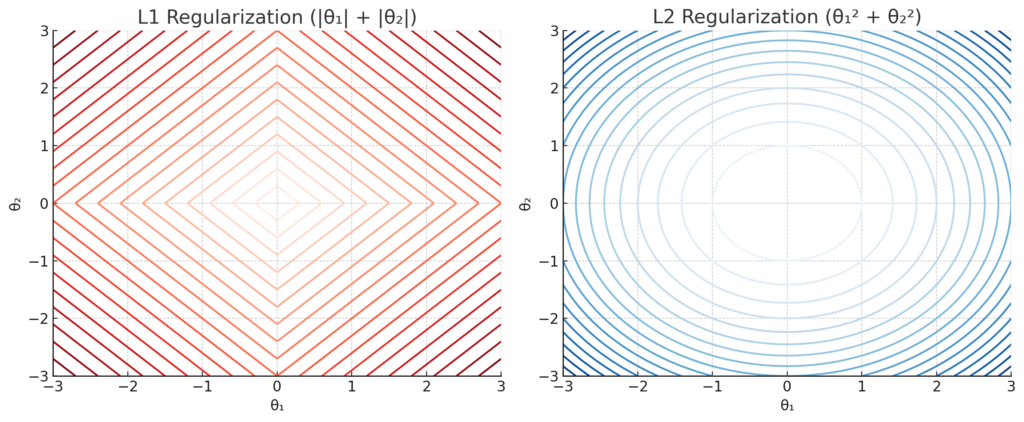
- 実線：Lasso（角ばったひし形）
→ Lassoは「角」でピタッとゼロにしやすい構造！
どちらを使えばよいのか？
| 条件 | 推奨手法 |
|---|---|
| 特徴量が多く、重要なものを選びたい | Lasso回帰 |
| すべての特徴量がそれなりに効いている | Ridge回帰 |
| 両方の良さを取り入れたい | ElasticNet |
ElasticNetはL1とL2をミックスした手法です。
次に何を学べばいい？
- scikit-learnでLassoとRidgeを実装してみる
- 正則化パラメータ 交差検証（Cross Validation）でチューニング
- ElasticNetやBayesian Ridgeなどの派生手法にもトライ！
まとめ：アルゴリズムの性格が見えてくる！
| 名前 | 数学的特徴 | 直感的イメージ |
|---|---|---|
| Lasso | L1正則化 | 重要な特徴量だけ選ぶ |
| Ridge | L2正則化 | 全体をなだらかに抑える |
| ElasticNet | L1 + L2 | 両者の良いとこ取り |
生成AI研修のおすすめメニュー
投稿者プロフィール
- 代表取締役
-
セイ・コンサルティング・グループ株式会社代表取締役。
岐阜県出身。
2000年創業、2004年会社設立。
IT企業向け人材育成研修歴業界歴20年以上。
すべての無駄を省いた費用対効果の高い「筋肉質」な研修を提供します！
この記事に間違い等ありましたらぜひお知らせください。
