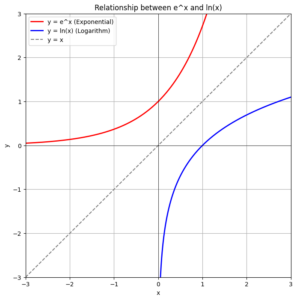
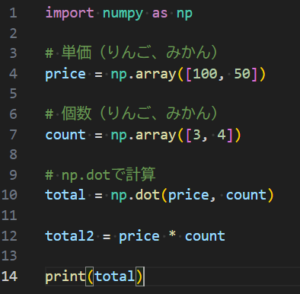
【デジタルなのにアナログ？】0と1の世界「情報科学」で、なぜネイピア数が支配者なのか

2026年1月13日 2026年1月13日山崎講師

山崎講師

こんにちは。ゆうせいです。

みなさんは「情報科学（コンピューターサイエンス）」と聞いて、どんな数字を思い浮かべますか？

おそらく、ほとんどの方が「 $0$ 」と「 $1$ 」を思い浮かべるでしょう。

スイッチのオンとオフ、電気が流れるか流れないか。デジタルな世界は、この二つの数字ですべてが構成されています。カクカクとした、白黒はっきりした世界です。

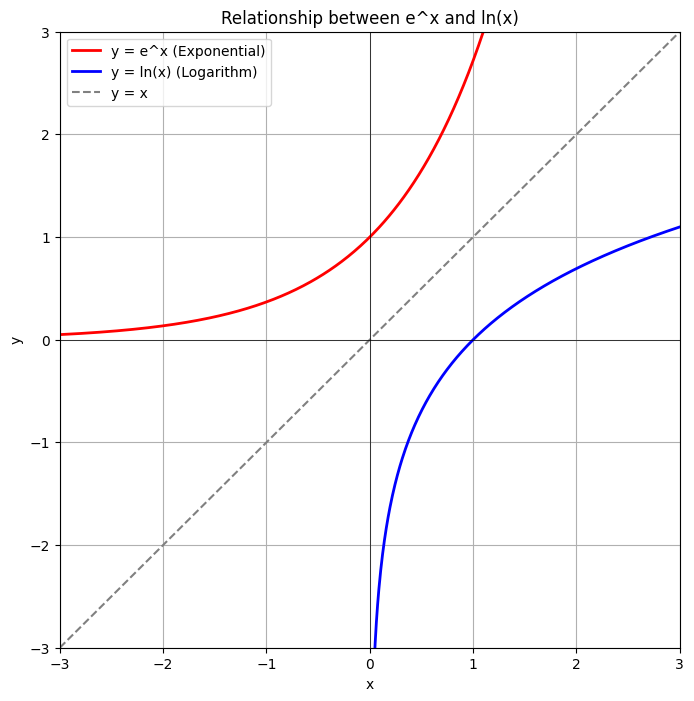
一方で、これまでお話ししてきた「ネイピア数 $e$ （約 $2.718$ ）」は、植物の成長や曲線の美しさを表す、とても滑らかでアナログな数字です。

「カクカクしたデジタルの世界に、なんでそんな中途半端な数字が出しゃばってくるの？」

そう思うのが自然です。しかし、実は情報科学の理論の根底には、どっしりとネイピア数が座っているのです。

きょうは、コンピュータの「0と1」の裏側で暗躍するネイピア数の物語を、専門用語を噛み砕きながらお話しします。

そもそも情報って「量」で測れるの？

情報科学の父と呼ばれるクロード・シャノンという天才がいました。彼はこう考えました。

「情報の『中身』ではなく、『量』を数学で計算できないだろうか？」

たとえば、「明日、太陽が東から昇るよ」と言われても、「へぇ、そうだね」としか思いませんよね。これは当たり前のことすぎて、情報の価値（量）は低くなります。

でも、「明日、宇宙人が家の前に着陸するよ」と言われたらどうでしょう？これはとんでもない衝撃です。つまり、情報の価値（量）が大きいと言えます。

シャノンは、この「驚きの度合い」を計算式にしました。これを「情報エントロピー」と呼びます。

ここで登場するのが、我らがネイピア数を使った「対数（ $\log$ ）」なんです。

情報量の単位は「ビット」だけじゃない

みなさんがよく聞く「ビット（bit）」は、 $2$ を基準（底）にした単位です。 $0$ か $1$ か、という二択の世界ですね。

しかし、情報科学の理論研究や、複雑な計算をするシミュレーションの世界では、「ナット（nat）」という単位が使われることがあります。

これは、ネイピア数 $e$ を基準にした情報の単位です。

$1$ nat $= 1.44$ bit

おおよそこれくらいの関係です。

「なんでわざわざ単位を変えるの？ややこしい！」と思いますよね。

例えるなら、ビットは「メートル」で、ナットは「ヤード」のようなものです。測っているものは同じ「情報」ですが、計算式を変形したり、微分（分析）したりするときには、ネイピア数ベースの「ナット」を使って計算するほうが、数式が圧倒的にシンプルで美しくなるのです。

「データのばらつき」を表す正規分布

情報科学は、データサイエンスとも密接に関わっています。

大量のデータを集めたとき、そのデータはどのような形になるでしょうか。

たとえば、あるWebサイトへのアクセス数や、ネットワーク通信の遅延時間、あるいは工場で作られた部品の微妙なサイズ誤差。

これらを集めてグラフにすると、平均値を中心にして、左右になだらかに広がる「釣鐘型（ベルカーブ）」の形になることがよくあります。これを「正規分布（ガウス分布）」と言います。

この「よくあるありふれた形」を表す数式の中に、実はネイピア数が隠れています。

確率の密度 $= \frac{1}{\sqrt{2\pi}} e^{-\frac{x^2}{2}}$

うわっ、複雑そう！と逃げないでください。

大事なのは、この式の中心に $e$ がいるということです。

なぜここに $e$ が？

$e^{-x^2}$ という部分は、「中心（ $0$ ）から離れれば離れるほど、急激に確率が減っていく」という様子を表しています。

通信エラーが起きる確率は低い
平均的なアクセス数が一番多い
極端に身長が高い人は少ない

こうした「自然なばらつき」を表現するのに、ネイピア数の「滑らかに減衰していく性質」がピッタリ当てはまるのです。

AIが画像を認識するときも、音声認識でノイズを除去するときも、裏側ではこの「正規分布（とネイピア数）」を使って、どれが正常でどれが異常かを判断しています。

メリットとデメリット

情報科学におけるネイピア数の役割を整理してみましょう。

メリット

理論計算が簡単になる複雑なアルゴリズムや通信の理論を組み立てるとき、微分や積分の計算が必須になります。ここで $e$ を基準にしておくと、計算途中で余計な係数が出ず、思考の邪魔をされません。
自然現象のシミュレーションに強いコンピュータの中で物理現象や生物の動きを再現しようとすると、自然界の法則であるネイピア数が必然的に必要になります。

デメリット

コンピュータのハードウェアとは相性が悪いコンピュータの回路自体はON/OFFの「2進数」で動いています。そのため、ネイピア数を使った理論を実際にプログラムで動かすときは、最終的に「0と1」の計算に翻訳（近似計算）する手間が発生します。
直感的にわかりにくい「情報量が $10$ ビットだ」と言われれば「 $2$ の $10$ 乗通りだな」とイメージできますが、「情報量が $10$ ナットだ」と言われても、どれくらいの規模なのか人間にはピンときません。

まとめ：デジタルと自然をつなぐ架け橋

いかがでしたか？

「情報科学」というデジタルな響きの中にも、実はとても人間臭い、あるいは自然界そのものである「ネイピア数」が息づいていることを感じていただけたでしょうか。

コンピュータは $0$ と $1$ で計算しますが、そのコンピュータを使って解き明かしたい問題（天気予報、株価予測、自然言語処理など）は、すべてネイピア数が支配する「複雑で滑らかな世界」の出来事です。

だからこそ、デジタル（コンピュータ）とアナログ（現実世界）をつなぐ通訳として、ネイピア数が必要不可欠なんですね。

今後の学習への指針

もしあなたがプログラミングを学んでいるなら、Pythonなどで「乱数（ランダムな数）」を作る関数を使ってみてください。

random.gauss() などの関数を使えば、今回紹介した「正規分布」に従う乱数を作ることができます。

画面の中に描かれた無機質なグラフが、ネイピア数の力によって、まるで自然界の現象のように生き生きとした分布を見せる様子は、とても感動的ですよ。

デジタルな技術を使いこなしつつ、その根底にある数学的な美しさも愛せるエンジニアを目指していきましょう！

セイ・コンサルティング・グループでは新人エンジニア研修のアシスタント講師を募集しています。

投稿者プロフィール

山崎講師代表取締役

セイ・コンサルティング・グループ株式会社代表取締役。
岐阜県出身。
2000年創業、2004年会社設立。
IT企業向け人材育成研修歴業界歴20年以上。
すべての無駄を省いた費用対効果の高い「筋肉質」な研修を提供します！
この記事に間違い等ありましたらぜひお知らせください。

学生時代は趣味と実益を兼ねてリゾートバイトにいそしむ。長野県白馬村に始まり、志賀高原でのスキーインストラクター、沖縄石垣島、北海道トマム。高じてオーストラリアのゴールドコーストでツアーガイドなど。現在は野菜作りにはまっている。

【デジタルなのにアナログ？】0と1の世界「情報科学」で、なぜネイピア数が支配者なのか