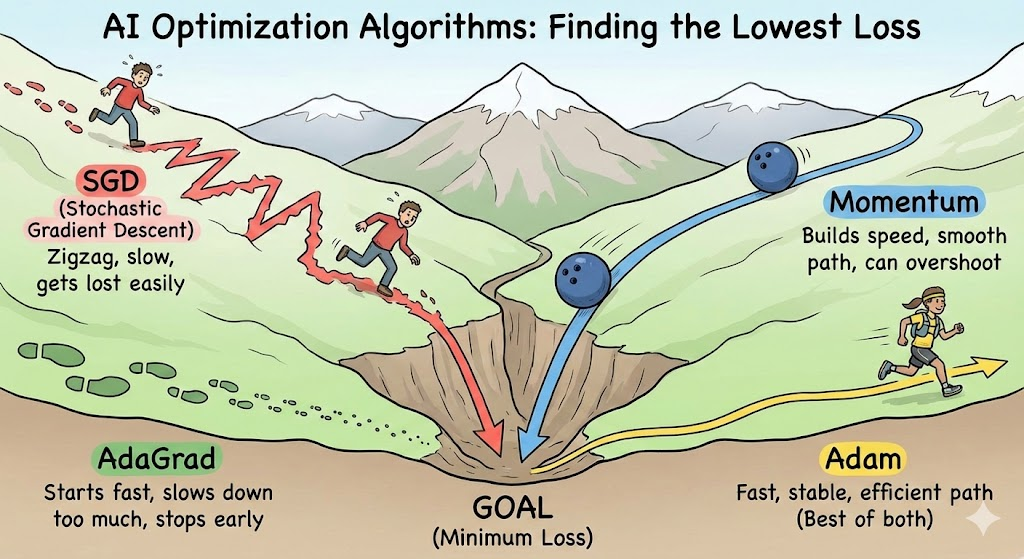
【数式で納得】AI学習の仕組みが見える！損失関数のパラメータ最適化手法4選

2026年1月17日 2026年1月17日山崎講師

山崎講師

こんにちは。ゆうせいです。

前回は、AIが賢くなるための「パラメータ最適化」について、イメージ重視で解説しました。今回はそこから一歩踏み込んで、エンジニアとして避けては通れない「数式」を交えて解説します。

「うわ、数式か……」と身構えないでくださいね。数式は、AIが行っている計算を地図のように記しただけのものです。記号の意味さえ分かれば、実は言葉で説明されるよりもずっとスッキリと理解できることが多いのです。

今回は、高校数学レベルの知識で理解できるように、一つひとつ丁寧に紐解いていきます。数式が読めるようになると、論文や技術書を読むのが楽しくなりますよ。

それでは、一緒に見ていきましょう。

最初に覚えておきたい3つの記号

各手法の解説に入る前に、共通して登場する記号を定義しておきます。これさえ覚えておけば、あとはパズルのようなものです。

$w$ ：重み（パラメータ）AIが学習して調整したい値そのものです。これを最適な値にすることがゴールです。
$\eta$ （エータ）：学習率1回の学習でどれくらい大きく値を更新するかを決める「歩幅」です。人間が設定します。
$g$ ：勾配（傾き）損失関数の傾きです。「どちらに進めば損失（エラー）が減るか」を教えてくれる羅針盤です。数式では $\frac{\partial L}{\partial w}$ と書かれることもありますが、ここではシンプルに $g$ とします。

1. SGD（確率的勾配降下法）

まずは基本のSGDです。

数式

$w_{t+1} = w_t - \eta g_t$

解説

とてもシンプルですね。この式は「今の重み $w_t$ から、傾き $g_t$ に歩幅 $\eta$ を掛けた分だけ引く」という意味です。

傾き $g_t$ がプラス（上り坂）なら、引くことでマイナス方向（下り坂）に進みます。逆に傾きがマイナスなら、引くことでプラス方向に進みます。つまり、常に「坂を下る方向」へ素直に進む式になっています。

特徴

計算が単純で分かりやすいですが、傾き $g$ にそのまま従うため、傾きが急な場所では大きく飛び、緩やかな場所ではほとんど進まないという、少し不器用な動きをします。

コード

class SGD:
    def __init__(self, lr=0.01):
        self.lr = lr

    def update(self, params, grads):
        """
        params: 重みパラメータの辞書 (例: {'W1': array, 'b1': array, ...})
        grads: 勾配の辞書 (paramsと同じキーを持つ)
        """
        for key in params.keys():
            params[key] -= self.lr * grads[key]

2. Momentum（モーメンタム）

次は、SGDに「勢い」を加えたMomentumです。

数式

まず、「速度」を表す変数 $v$ を計算します。

$v_t = \alpha v_{t-1} - \eta g_t$

次に、その速度を使って重みを更新します。

$w_{t+1} = w_t + v_t$

（ $\alpha$ は慣性係数といって、どれくらい過去の勢いを残すかを決める値です）

解説

1行目の式を見てください。今回の速度 $v_t$ は、前回の速度 $v_{t-1}$ （過去の勢い）に、今回の傾きによる加速 $- \eta g_t$ を足して決まります。

そして2行目で、その計算された速度の分だけ重み $w$ が移動します。

特徴

過去の速度 $v_{t-1}$ が式に含まれているのがポイントです。これにより、坂道を転がるボールのように加速がつきます。谷底付近で傾き $g$ が小さくなっても、勢い $v$ が残っているため、止まらずに進むことができます。

コード

class Momentum:
    def __init__(self, lr=0.01, momentum=0.9):
        self.lr = lr
        self.momentum = momentum
        self.v = None  # 速度(velocity)

    def update(self, params, grads):
        # 初回のみvを初期化
        if self.v is None:
            self.v = {}
            for key, val in params.items():
                self.v[key] = np.zeros_like(val)

        for key in params.keys():
            # v = momentum * v - lr * grad
            self.v[key] = self.momentum * self.v[key] - self.lr * grads[key]
            # W = W + v
            params[key] += self.v[key]

3. AdaGrad（アダグラッド）

続いて、歩幅を自動調整するAdaGradです。

数式

まず、過去の傾きの大きさを蓄積する変数 $h$ を更新します。

$h_t = h_{t-1} + g_t^2$

次に、その $h$ を使って重みを更新します。

$w_{t+1} = w_t - \frac{\eta}{\sqrt{h_t} + \epsilon} g_t$

（ $\epsilon$ はゼロ除算を防ぐための非常に小さな数です）

解説

ポイントは分母にある $\sqrt{h_t}$ です。

$h_t$ には、過去の傾き $g$ の2乗がどんどん足されていきます。つまり、これまでたくさん更新されてきた（傾きが大きかった）パラメータほど、 $h_t$ は大きくなります。

分母が大きくなるということは、分数全体（更新量）は小さくなりますよね。

つまり、「これまでたくさん動いたパラメータは、もうゴールに近いだろうから、これからの更新量（歩幅）を小さくしよう」というブレーキの役割を数式が果たしているのです。

特徴

パラメータごとに個別に学習率を調整してくれる賢い式ですが、学習が進むにつれて $h_t$ が無限に大きくなり、最終的に更新量が限りなく $0$ になって学習が止まってしまう欠点があります。

コード

class AdaGrad:
    def __init__(self, lr=0.01):
        self.lr = lr
        self.h = None  # 過去の勾配の二乗和

    def update(self, params, grads):
        if self.h is None:
            self.h = {}
            for key, val in params.items():
                self.h[key] = np.zeros_like(val)

        for key in params.keys():
            # 勾配の二乗を加算 (h += grad * grad)
            self.h[key] += grads[key] * grads[key]
            
            # パラメータ更新 (ゼロ除算を防ぐために1e-7を加える)
            params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7)

4. Adam（アダム）

最後に、現在主流のAdamです。MomentumとAdaGradの考え方を合体させたような式になります。

数式

少し複雑に見えますが、要素に分解すれば大丈夫です。

まず、Momentumのように「勢い（傾きの平均）」を計算します（ $m$ ）。

$m_t = \beta_1 m_{t-1} + (1 - \beta_1) g_t$

次に、AdaGradのように「過去の変動の大きさ（傾きの2乗の平均）」を計算します（ $v$ ）。

$v_t = \beta_2 v_{t-1} + (1 - \beta_2) g_t^2$

最後に、これらを使って重みを更新します。

$w_{t+1} = w_t - \eta \frac{\hat{m}_t}{\sqrt{\hat{v}_t} + \epsilon}$

（ $\hat{m}, \hat{v}$ は、初期値の影響をなくすための補正を行った値ですが、ここでは $m, v$ と似たものと考えてください）

解説

最後の更新式を見てください。

分子には $m$ （勢い）があり、分母には $\sqrt{v}$ （変動の大きさ）があります。

つまり、「勢いに乗って進みつつ（Momentumの要素）、変動が激しいパラメータは歩幅を抑える（AdaGradの要素）」という調整を同時に行っているのです。

特徴

数式は少し多いですが、やっていることは「適切な方向へ、適切な歩幅で進む」ための合理的な計算です。これが、多くのタスクでAdamが安定して良い結果を出す理由です。

コード

class Adam:
    def __init__(self, lr=0.001, beta1=0.9, beta2=0.999):
        self.lr = lr
        self.beta1 = beta1
        self.beta2 = beta2
        self.iter = 0
        self.m = None # モメンタム（1次モーメント）
        self.v = None # 適合的な学習率（2次モーメント）
        
    def update(self, params, grads):
        if self.m is None:
            self.m, self.v = {}, {}
            for key, val in params.items():
                self.m[key] = np.zeros_like(val)
                self.v[key] = np.zeros_like(val)
        
        self.iter += 1
        
        # バイアス補正のための学習率調整
        lr_t  = self.lr * np.sqrt(1.0 - self.beta2**self.iter) / (1.0 - self.beta1**self.iter) 
        
        for key in params.keys():
            # mの更新
            self.m[key] += (1 - self.beta1) * (grads[key] - self.m[key])
            # vの更新
            self.v[key] += (1 - self.beta2) * (grads[key]**2 - self.v[key])
            
            # パラメータ更新
            params[key] -= lr_t * self.m[key] / (np.sqrt(self.v[key]) + 1e-7)

まとめ

今回は数式を交えて4つの手法を解説しました。

SGD ： $w - \eta g$ （シンプルに傾き方向へ）
Momentum ： $w + v$ （速度と慣性を利用）
AdaGrad ： $\frac{1}{\sqrt{h}}$ で割る（過去の動きに応じてブレーキ）
Adam ：分子に勢い、分母にブレーキ（両者のいいとこ取り）

数式を見ると、それぞれのアルゴリズムが「何を重視して動いているか」が、より明確に見えてきませんか。プログラムの中では、これらの数式が高速で計算され、AIが賢くなっているのです。

さて、数式の意味が分かったところで、次のステップです。

実際にPyTorchなどのフレームワークの公式ドキュメント（Source code）を開いて、今日見た数式がどのようにプログラムコードとして書かれているか確認してみませんか。

「あ！この行はこの数式のことだ！」と発見できたとき、エンジニアとしての視界が一気に開けますよ。ぜひ挑戦してみてください。

セイ・コンサルティング・グループでは新人エンジニア研修のアシスタント講師を募集しています。

投稿者プロフィール

山崎講師代表取締役

セイ・コンサルティング・グループ株式会社代表取締役。
岐阜県出身。
2000年創業、2004年会社設立。
IT企業向け人材育成研修歴業界歴20年以上。
すべての無駄を省いた費用対効果の高い「筋肉質」な研修を提供します！
この記事に間違い等ありましたらぜひお知らせください。

学生時代は趣味と実益を兼ねてリゾートバイトにいそしむ。長野県白馬村に始まり、志賀高原でのスキーインストラクター、沖縄石垣島、北海道トマム。高じてオーストラリアのゴールドコーストでツアーガイドなど。現在は野菜作りにはまっている。