なぜ統計学に「円周率」が出てくるの？正規分布に隠された真ん丸な秘密
山崎講師こんにちは。ゆうせいです。
前回、前々回と、ガンマ関数やネイピア数 
でも、統計学を学んでいると、誰もが一度は抱く「最大の疑問」があります。それは、正規分布の式になぜ円周率 
「円周率は、円の長さや面積を求めるためのものでしょ？ データのバラつきと何の関係があるの？」
今日は、そんな皆さんのモヤモヤを、とっても直感的なイメージで解き明かしていきたいと思います！
1. そもそも 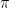とは何だったか
まずは基本に立ち返りましょう。円周率とは、円の直径に対する円周の長さの比率、約 3.14 です。
私たちは小学校以来、「丸いもの」を測るときには必ずこれを使ってきました。しかし、統計学の正規分布は「山なりのカーブ」です。どこにも「円」なんて見当たりませんよね？
実は、この「山」を下から見上げたり、回転させたりすると、驚くべき光景が見えてくるんです。
2. 山を回転させると「円」が現れる！
正規分布の合計面積を 1 にするための計算（積分）をするとき、数学者たちはある工夫をしました。
ひとつの正規分布の山（2次元）を、もうひとつの正規分布と組み合わせて、立体的な「お椀をひっくり返したような形」（3次元）を想像したのです。
この立体を真上から見ると、なんと、どの方向から見ても綺麗な「正円」になっていることが分かります。中心から等しい距離にある点は、同じ確率（高さ）を持っているからです。
この「確率の山」が円形に広がっているため、その体積や面積を計算しようとすると、どうしても円の性質を無視できなくなります。その結果、計算の最終段階で
つまり、正規分布の式に
3. 円周率が統計にいるメリット・デメリット
| 項目 | メリット | デメリット |
| 数学的な調和 | 物理法則や自然現象の多くが円形や球形の対称性を持つため、現実を正確に模写できる | 「なぜここで 3.14 なの？」という初心者の混乱を招きやすい |
| 極限の正確性 | データの数が無限に増えると、どんなバラつきもこの「円の秩序」に収束していく | 手計算で円周率を扱うのは面倒で、コンピュータ前提の式になる |
4. 全てがつながる瞬間
ここで、以前お話しした「ガンマ君」を思い出してください。
正規分布の式に含まれる 
- Γ（ガンマ） が、それらを矛盾なく一つの式にまとめ上げる。
どうでしょう。バラバラだった記号たちが、ひとつのチームとして動いているように見えてきませんか？
これからの学習へのアドバイス
- 「対称性」を意識する：左右対称の形を見たら、「どこかに円の性質が隠れているかも？」と疑ってみてください。
- ガウス積分を調べてみる：もし数学に自信があれば、「ガウス積分」という言葉で検索して、どうやって
- 自然界の不思議を感じる：ランダムな出来事の積み重ねが、最終的に円という最も完璧な図形のルールに従う。その神秘に触れるだけで、統計学はもっと面白くなります！
「円周率は円だけのものじゃない」。この事実に気づけたあなたは、もう数式の見た目に惑わされることはありません。
皆さんは、この
セイ・コンサルティング・グループでは新人エンジニア研修のアシスタント講師を募集しています。
投稿者プロフィール
- 代表取締役
-
セイ・コンサルティング・グループ株式会社代表取締役。
岐阜県出身。
2000年創業、2004年会社設立。
IT企業向け人材育成研修歴業界歴20年以上。
すべての無駄を省いた費用対効果の高い「筋肉質」な研修を提供します！
この記事に間違い等ありましたらぜひお知らせください。
学生時代は趣味と実益を兼ねてリゾートバイトにいそしむ。長野県白馬村に始まり、志賀高原でのスキーインストラクター、沖縄石垣島、北海道トマム。高じてオーストラリアのゴールドコーストでツアーガイドなど。現在は野菜作りにはまっている。
