もう怖くない！統計学の不思議な文字「ガンマ」をマスターしよう

2026年2月7日 最終更新日時 : 2026年2月7日 山崎講師山崎講師

もう怖くない！統計学の不思議な文字「ガンマ」をマスターしよう

こんにちは。ゆうせいです。

統計学を勉強していると、避けては通れない壁がいくつかありますよね。その中でも、多くの初心者を立ち止まらせるのが、ギリシャ文字の「Γ（ガンマ）」ではないでしょうか。

見た目はまるで「L」を逆さにしたような、あるいは「カタカナのフ」のような不思議な形をしています。教科書を開いてこの文字が出てきた瞬間、そっと本を閉じたくなる気持ち、よく分かります。でも、安心してください。今日はこのガンマが、実は私たちの生活を支えるデータ分析に欠かせない、とっても便利な道具であることをお話しします！

ガンマ（Γ）の正体は「超すごい階乗」

皆さんは、高校の数学で「階乗（かいじょう）」を習ったのを覚えていますか？

例えば、3! は 3 \times 2 \times 1 = 6 ですし、5! は 5 \times 4 \times 3 \times 2 \times 1 = 120 ですね。このように、整数を階段のように掛け合わせていくのが階乗です。

ところが、統計の世界では「2.5の階乗」といった、整数ではない中途半端な数字の計算が必要になる場面が出てきます。困りましたよね。整数でしかないはずの階段を、スロープのようにつなげて計算できるように拡張したもの。それこそがガンマ関数なのです！

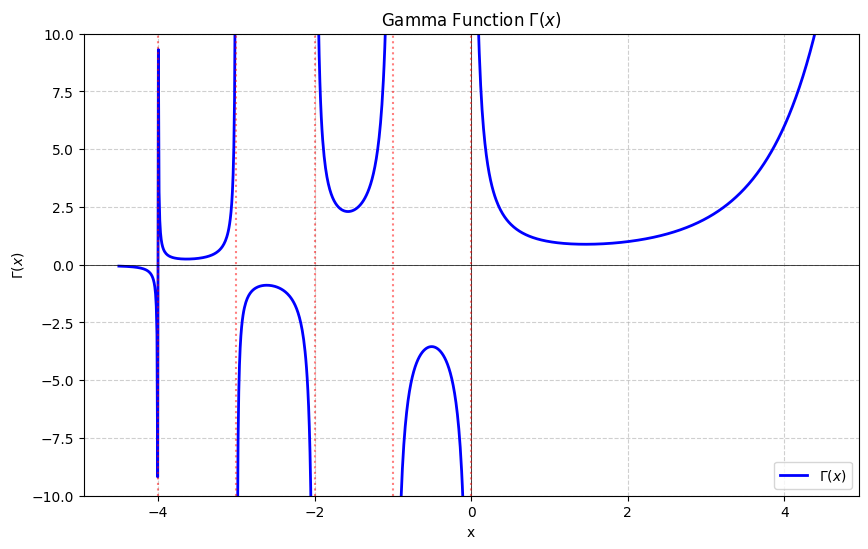
ガンマ関数の魔法のルール

ガンマ関数には、とってもシンプルなルールがあります。

\Gamma(n) = (n - 1)!

例えば、 \Gamma(4) を計算したいときは、 (4 - 1)! = 3 \times 2 \times 1 = 6 となります。

なぜ - 1 をするのか不思議に思うかもしれませんが、これは数学的な歴史の積み重ねで決まったルールなので、今は「1つ手前の数字の階乗を計算するんだな」と軽く捉えておくだけで十分ですよ！

なぜ統計学で「ガンマ」が必要なの？

さて、このガンマ関数を使って作られるのがガンマ分布です。これは「ある出来事が起こるまでの待ち時間」を分析するのに使われます。

例えば、コールセンターに電話がかかってくるまでの時間や、機械が故障するまでの期間など、私たちの周りには「待ち時間」に関するデータが溢れています。

ガンマ分布は、以前お話ししたλ（ラムダ）という「平均的な回数」を表す記号と組み合わせて、次のような場面で活躍します。

  • 銀行の窓口に5人の客が来るまでにかかる時間の予測
  • 部品が摩耗して動かなくなるまでの寿命の計算

1. ガンマ分布の式：待ち時間を操る魔法

まずは、ガンマの名の通り「ガンマ分布」の確率密度関数を見てみましょう。

f(x) = \frac{\lambda^{k}}{\Gamma(k)} \times x^{k-1} \times e^{-\lambda \times x}

「うわあ、逃げ出したい！」と思いましたか？ ちょっと待ってください！ 注目してほしいのは、分母にいる \Gamma(k) です。

ここでガンマ君が何をしているかというと、実は「全体のバランス調整（正規化）」をしています。 確率の世界では、すべての可能性を足すと合計が1（100％）にならなければいけません。この式の右側（ x や e が出てくる部分）だけだと、合計が1にならないんです。

そこで、分母にガンマ関数を置くことで、「はい、これで合計がちゃんと1になりますよ」と帳尻を合わせているわけです。いわば、オーケストラの指揮者のような役割ですね。

2. カイ二乗分布：バラつきを分析する式

次に紹介するのは、検定などでよく使われる「カイ二乗分布」です。

f(x) = \frac{1}{2^{k/2} \times \Gamma(k/2)} \times x^{k/2 - 1} \times e^{-x/2}

ここでも分母に \Gamma(k/2) がいますね！ カイ二乗分布は、データの「バラつき（分散）」がどんなルールで動いているかを調べるためのものです。

ここで k/2 という中途半端な数字が出てきても、ガンマ関数がいれば安心。さきほどお話しした「スロープのような階乗」の機能を使って、どんな自由度（ k ）に対しても、きっちり確率を計算してくれるんです。

もしガンマ君がいなかったら、自由度が奇数のときに計算が止まってしまうかもしれません。彼のおかげで、私たちはどんなデータでもスムーズに分析できるというわけです。

3. t分布の数式：平均の推測を支える守護神

この記事のシリーズで最初にお話しした「t分布」を覚えていますか？実は、あのt分布の確率を決める複雑な数式の中にも、ガンマ君は隠れているんです。

f(t) = \frac{\Gamma((v+1)/2)}{\sqrt{v \times \pi} \times \Gamma(v/2)} \times (1 + t^{2}/v)^{-(v+1)/2}

いきなりものすごい式が出てきましたね！でも、ビビる必要はありません。 ここで注目してほしいのは、分母と分子の両方にガンマ君がいることです。

自由度 v という数字がどんな値になっても、この分数の部分が「重り」となって全体の面積を1に調整してくれます。t分布が正規分布よりも少し裾が長くて、中心が少し低い形を保っていられるのは、このガンマ君たちが絶妙なバランスで数値をコントロールしてくれているおかげなのです。

4. ベータ分布の式：A/Bテストの裏側にいる立役者

次に、マーケティングやWebサイトの改善（A/Bテスト）などでよく使われる「ベータ分布」を紹介します。この分布は「成功確率」を予想するのが得意なのですが、ここにもガンマ君の影があります。

ベータ分布の核となる「ベータ関数 B(\alpha, \beta) 」は、実はガンマ関数を使って次のように書けるんです。

B(\alpha, \beta) = \frac{\Gamma(\alpha) \times \Gamma(\beta)}{\Gamma(\alpha + \beta)}

これは「ベータ君とガンマ君の協力関係」と言えるでしょう。 成功回数を \alpha 、失敗回数を \beta としたとき、ガンマ関数がそれらを階乗のように掛け合わせたり割ったりして、綺麗な確率のグラフを描き出してくれます。

ガンマ分布のメリットとデメリット

ガンマ分布を使いこなせると、どんな良いことがあるのでしょうか。

項目メリットデメリット
ガンマ分布待ち時間や寿命など、0以上の連続したデータを扱うのが大得意計算式が複雑で、手計算には向かない
柔軟性形（形状パラメータ）を自由に変えられるので、様々なデータにフィットする初心者には直感的にイメージしづらい

記号に振り回されないコツ

統計学に登場する記号たちは、どれも「複雑な現象をたった一文字で表現したい」という先人たちの知恵から生まれています。

もし今後、数式の中に「Γ」を見つけたら、「ああ、あの中途半端な数字の階乗を計算してくれる便利なスロープのことね！」と思い出してください。そう考えるだけで、少しだけ数式が優しく見えてきませんか？

これからの学習のステップ

今日の研修で、ガンマの見た目への恐怖心は消えたはずです。次のステップとして、以下のことに挑戦してみましょう！

  • ガンマ分布とよく似た「指数分布」との違いを調べてみてください。
  • エクセルやGoogleスプレッドシートで「GAMMA関数」を実際に入力して、数字がどう変わるか遊んでみましょう。
  • 正規分布以外の「山の形」にはどんな種類があるのか、パラパラと図鑑を眺めるように探してみてください。

統計学は、一つひとつの記号と仲良くなることで、霧が晴れるように理解が進みます。

皆さんは、この「Γ」以外に、見ていて不安になるような記号はありますか？もしあれば、ぜひ教えてください。また分かりやすく解説しますね！

セイ・コンサルティング・グループでは新人エンジニア研修のアシスタント講師を募集しています。

投稿者プロフィール

山崎講師
山崎講師代表取締役
セイ・コンサルティング・グループ株式会社代表取締役。
岐阜県出身。
2000年創業、2004年会社設立。
IT企業向け人材育成研修歴業界歴20年以上。
すべての無駄を省いた費用対効果の高い「筋肉質」な研修を提供します！
この記事に間違い等ありましたらぜひお知らせください。

学生時代は趣味と実益を兼ねてリゾートバイトにいそしむ。長野県白馬村に始まり、志賀高原でのスキーインストラクター、沖縄石垣島、北海道トマム。高じてオーストラリアのゴールドコーストでツアーガイドなど。現在は野菜作りにはまっている。
対象読者
新人エンジニア研修講師
前の記事
データが語る真実の見つけ方！パラメトリック統計学で推測の達人になろうNew!!
2026年2月7日
次の記事
なぜ統計学に「円周率」が出てくるの？正規分布に隠された真ん丸な秘密New!!
2026年2月7日