近似曲線と相関係数の関係を式にすると?
近似曲線と相関係数の関係を式にすると、次のような形で表すことができます。
1. 近似曲線の基本
まず、近似曲線とは、与えられたデータ点の集合に対して、そのデータの分布を最もよく表す曲線を指します。この曲線を用いることで、データのトレンドや将来の予測を行うことが可能です。
例えば、線形近似では、直線の方程式
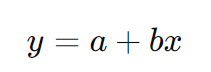
がよく使われます。ここで、a は切片、bは傾きです。
2. 相関係数の定義
相関係数(Pearsonの積率相関係数)は、2つの変数間の線形関係の強さを示す指標です。相関係数 rは次の式で定義されます。

3. 近似曲線と相関係数の関係
線形近似の場合、近似曲線の傾き bbb と相関係数 rrr との関係は次の式で表されます。

この式は、相関係数 rrr がデータの変数間の相関の強さを表し、その相関の強さが近似曲線の傾きに直接影響を与えることを示しています。
具体例
例えば、身長 xxx と体重 yyy との間に強い正の相関(rrr が1に近い)がある場合、傾き bbb は正の大きな値を取ることになります。逆に、相関が弱い(rrr が0に近い)場合、傾き bbb は小さくなり、近似曲線はほぼ水平に近づきます。
まとめと今後の学習の指針
近似曲線と相関係数の関係は、データの傾向を理解する上で非常に重要です。相関係数が高ければ高いほど、近似曲線はデータの分布をよく表し、予測や分析がしやすくなります。逆に、相関係数が低い場合は、近似曲線の傾きは小さくなり、データの分布をうまく表せない可能性があります。
このような基本的な関係を理解することで、データ解析のスキルを向上させることができます。今後は、非線形の近似曲線や他の相関係数(例えばスピアマンの順位相関係数)についても学習を進めると良いでしょう。
投稿者プロフィール

- 代表取締役
-
セイ・コンサルティング・グループ株式会社代表取締役。
岐阜県出身。
2000年創業、2004年会社設立。
IT企業向け人材育成研修歴業界歴20年以上。
すべての無駄を省いた費用対効果の高い「筋肉質」な研修を提供します!
この記事に間違い等ありましたらぜひお知らせください。
学生時代は趣味と実益を兼ねてリゾートバイトにいそしむ。長野県白馬村に始まり、志賀高原でのスキーインストラクター、沖縄石垣島、北海道トマム。高じてオーストラリアのゴールドコーストでツアーガイドなど。現在は野菜作りにはまっている。

