【数学アレルギー克服】機械学習で「ネイピア数」が愛される理由を、新人エンジニアのために語り尽くす
こんにちは。ゆうせいです。
エンジニアとしてのキャリアをスタートさせたばかりのあなた、毎日新しい技術に触れる中で、ふとこんな疑問を抱いたことはありませんか?
「なんで機械学習の参考書には、決まって『 』とかいう謎のアルファベットが出てくるんだろう?」
わかります。その気持ち、痛いほどわかります!今までプログラミング言語の文法やライブラリの使い方を必死に覚えてきたのに、急に数学の壁が立ちはだかると、心が折れそうになりますよね。
でも、ちょっと待ってください。実はこの こと「ネイピア数」、機械学習にとってはなくてはならない相棒であり、エンジニアの仕事を楽にしてくれる魔法の数字なんです。
きょうは、数式を見るだけで頭が痛くなる……というあなたのために、なぜ機械学習の世界でネイピア数がこれほどまでに愛されているのか、その理由を優しく、熱く解説していきます。
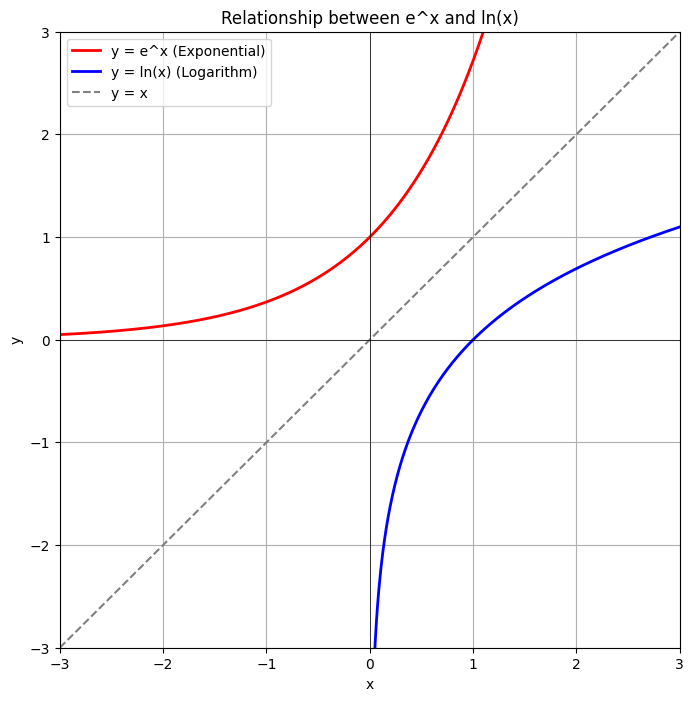
そもそもネイピア数って何モノ?
まずは、この不思議な数字の正体から暴いていきましょう。
ネイピア数とは、円周率の (パイ)と同じような、終わりのない無理数です。具体的には、およそ
という値を持ちます。数学の世界では、自然対数の底(てい)とも呼ばれていますね。
教科書的な定義を言えば「 円を
年間預けたとき、金利の計算回数を無限に増やしていったときの元利合計」なんて説明をされますが、今はそんな小難しいことは忘れてしまって構いません。
重要なのは、この数字が「成長」や「変化」を表すときに、自然界のあらゆる場所に顔を出すということです。細胞の分裂、ウイルスの感染拡大、そして温かいコーヒーが冷めていく温度変化。これらすべてに、ネイピア数が潜んでいるのです。
不思議だと思いませんか?人間が作ったわけでもないのに、世界の法則のあちこちに という数字が隠れているなんて!
なぜ機械学習エンジニアはネイピア数を愛するのか
では、ここからが本題です。なぜ、自然界の法則であるネイピア数が、人工知能である機械学習で使われるのでしょうか。
結論から言います。それは「計算が圧倒的にラクになるから」です。
究極の手抜きツールとしての微分
機械学習の学習プロセスをひとことで言うと、「誤差を最小にするためのパラメータ調整」です。予測と正解のズレ(誤差)を計算し、そのズレが小さくなるように数値を少しずつ動かしていきます。
この「どちらに動かせばズレが小さくなるか」を知るために使う道具が「微分」です。高校数学で習った、あの微分です。微分とは、ある時点での「変化の割合(傾き)」を求めることでしたね。
ここで、ネイピア数の魔法が発動します。
一般的な数字、たとえば を
乗した関数
を微分しようとすると、計算式の中に余計な係数が出てきてしまい、式が複雑になります。
ところが、ネイピア数 を使った関数
を微分すると、驚くべきことが起こります。
微分の結果
見てください!なんと、微分しても形がまったく変わらないのです。「今の値」がそのまま「変化のスピード」になる。これがネイピア数の最大の特徴であり、最強のメリットです。
例えるなら「変形しない工具」
想像してみてください。あなたはネジを締める仕事をしています。
普通の数字( や
)を使うのは、ネジを回すたびにドライバーの形が変わってしまい、いちいち持ち手を調整しなければならないようなものです。面倒ですよね?
一方で、ネイピア数を使うというのは、どんなに回しても形が変わらず、常に手になじむ最高のドライバーを使っている状態です。
機械学習、特にディープラーニングでは、何層にも重なった計算式を何度も何度も微分する必要があります(これを誤差逆伝播法と呼びます)。もし微分するたびに式が複雑になっていたら、計算時間が膨大になり、AIの学習は何年も終わらないかもしれません。
ネイピア数のおかげで、コンピュータは計算の負担を減らし、高速に学習を進められるのです。
具体的にどこで使われているの?
ネイピア数のありがたみがわかったところで、実際の現場でどう使われているかを見てみましょう。
シグモイド関数:あやふやな入力を白黒つける
ニューラルネットワークの活性化関数として有名な「シグモイド関数」。これは、入力を から
の間の数値にギュッと押し込める役割を持ちます。確率などを表すのによく使われますね。
この関数の正体も、実はネイピア数の塊です。
出力
式の中に が堂々と居座っていますね。
この関数を使うと、どんなに大きな数字が来ても に近づけ、どんなに小さな(マイナスの)数字が来ても
に近づけてくれます。そして何より、この関数は微分したときの計算式が非常にシンプルになるよう設計されているのです。
ここでも「計算のしやすさ」というメリットが最大限に活かされています。
ネイピア数を使うメリットとデメリット
ここで一度、情報を整理してみましょう。
メリット
- 微分しても形が変わらないため、計算コストが劇的に下がる。
- 連続的な変化を滑らかに表現できるため、確率や統計と相性が良い。
- 多くの数学的公式や物理法則と整合性が取れる。
デメリット
という中途半端な数字なので、直感的に大きさをイメージしにくい。
- 初心者にとっては、数式が出てきた時点で「難しそう」という心理的ハードルになる。
デメリットのほとんどは「人間の感覚」に関することです。コンピュータにとっては、 も
も単なる数値データに過ぎません。計算が楽になるなら、断然そちらを選びますよね。
まとめ:ネイピア数はエンジニアの味方だ!
いかがでしたか?
「ネイピア数」という名前の響きだけで敬遠していた が、実はエンジニアの仕事を裏で支える「縁の下の力持ち」であることが伝わったでしょうか。
機械学習の世界で を見かけたら、こう思ってください。
「おっ、ここでも計算を楽にするために頑張ってくれているんだな」と。
そう考えるだけで、難解な数式も少しだけ親しみやすく見えてくるはずです。
今後の学習への指針
ネイピア数への苦手意識が薄れたあなたに、次のステップを提案します。
まずは、Pythonの数値計算ライブラリである「NumPy」を使ってみましょう。
np.exp() という関数を使えば、自分で計算しなくてもコンピュータが一瞬でネイピア数の計算をしてくれます。
そして、実際にコードを書きながら、「シグモイド関数」をグラフに描画してみてください。あの美しいS字カーブが、ネイピア数によって作られていることを実感できるはずです。
数学は、エンジニアを苦しめるための道具ではありません。世界を記述し、未来を作るための最強の武器です。
さあ、あなたもネイピア数を武器にして、機械学習の深い森へと足を踏み入れてみましょう!
セイ・コンサルティング・グループでは新人エンジニア研修のアシスタント講師を募集しています。
投稿者プロフィール

- 代表取締役
-
セイ・コンサルティング・グループ株式会社代表取締役。
岐阜県出身。
2000年創業、2004年会社設立。
IT企業向け人材育成研修歴業界歴20年以上。
すべての無駄を省いた費用対効果の高い「筋肉質」な研修を提供します!
この記事に間違い等ありましたらぜひお知らせください。
学生時代は趣味と実益を兼ねてリゾートバイトにいそしむ。長野県白馬村に始まり、志賀高原でのスキーインストラクター、沖縄石垣島、北海道トマム。高じてオーストラリアのゴールドコーストでツアーガイドなど。現在は野菜作りにはまっている。