【新人エンジニア必見】ロジスティック曲線の名前の由来とは？物流とは関係ない意外な真実

2025年11月21日 2025年11月21日山崎講師

山崎講師

こんにちは。ゆうせいです。

みなさんは、機械学習や統計学を勉強していて「ロジスティック回帰」や「ロジスティック曲線」という言葉に出会ったことはありませんか？

エンジニアとしてデータを扱っていると、必ずと言っていいほど登場するこの関数。名前を聞いて、ふと疑問に思ったことはないでしょうか。

「ロジスティックって、あのトラックとか倉庫の『物流（ロジスティクス）』のこと？」

実は、多くの人がここで首をかしげます。配送ルートの計算でもするのかな、なんて想像してしまいますよね。でも、結論から言うと、この名前は物流とは直接関係がないのです！

今日は、なぜこのS字のカーブが「ロジスティック」と呼ばれるようになったのか、その意外な由来と歴史について、数式が苦手な方にもわかるように紐解いていきましょう。新人エンジニアのみなさん、この雑学を知っていると、先輩との会話が少し弾むかもしれませんよ。

ロジスティック曲線とは何か

由来の話をする前に、まずはこの曲線がどんなものか、簡単にイメージを共有しましょう。

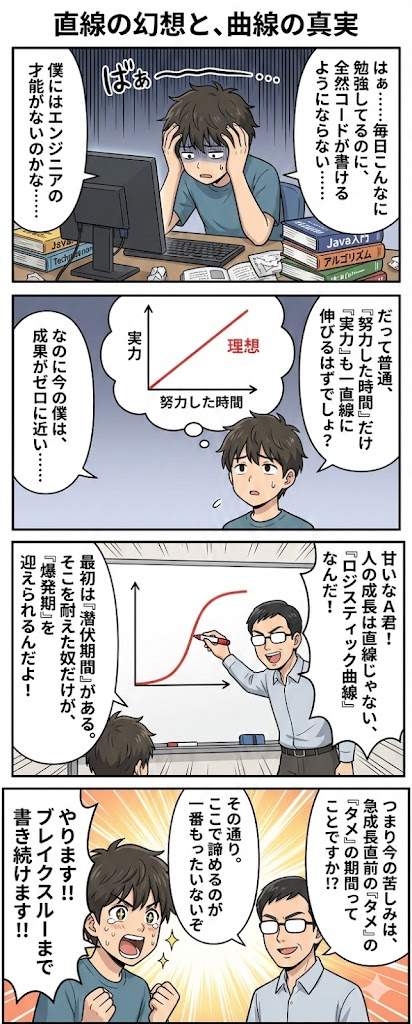
ロジスティック曲線とは、最初は勢いよく成長するけれど、ある限界に近づくと成長が緩やかになり、最終的には天井（上限）にピタリと張り付くような動きをする曲線のことです。形がアルファベットの「S」に似ていることから、シグモイド関数の一種としても知られています。

わかりやすい例を挙げてみましょう。

ある無人島に、つがいのウサギを放したと想像してください。

最初は敵もいないしエサも豊富なので、ウサギの数は爆発的に増えていきます。倍々ゲームのように増えるこの状態は、まさに指数関数的な増加です。

しかし、島には広さやエサの量に限りがありますよね？

ウサギが増えすぎると、次第にエサ不足になったり、住む場所がなくなったりします。すると、増加のスピードは徐々に落ちていき、最終的にはその島が養えるギリギリの数（環境収容力）で頭打ちになります。

このように、「最初は急成長するが、限界に近づくとブレーキがかかる」という現象を数式で表したのがロジスティック曲線なのです。

なぜ「ロジスティック」という名前なのか

では、本題に入りましょう。なぜこのS字カーブに「ロジスティック」という名前がついたのでしょうか。

この名前を付けたのは、19世紀のベルギーの数学者、ピエール＝フランソワ・フェルフルストです。彼は人口増加のモデルを研究していました。

当時、マルサスという経済学者が「人口は幾何級数的（指数関数的）に増加する」という有名な説を唱えていました。つまり、放っておけば人口は無限に増え続けるという考え方です。これを数学の世界では、対数（Logarithm）に関連付けて考えることが一般的でした。

しかし、フェルフルストは考えました。

「いやいや、現実には食料や土地に限界があるから、どこかで成長は止まるはずだ」

そこで彼は、無限に増え続けるカーブに対し、上限がある新しいカーブを考案しました。そして、その新しい曲線に「ロジスティック（Logistic）」という名前を与えたのです。

由来の有力な説：対数との対比

実は、フェルフルスト本人は「なぜロジスティックと名付けたか」を明確に書き残していません。ですが、最も有力な説は、「対数（Logarithm）」という言葉との対比で名付けたというものです。

当時の数学用語では、理論的な計算や算術のことを、ギリシャ語の「計算技術（Logistikos）」に由来する言葉で表現する文化がありました。

無限に発散していく「ロジスティックではない（対数的な）」曲線
現実的な計算に基づき、上限を持って収束する「ロジスティックな（計算巧みな）」曲線

このように、既存の理論（Logarithm）と韻を踏みつつ、対となる概念として「Logistic」という言葉を選んだのではないか、と言われています。つまり、物流の「Logistics」ではなく、古代ギリシャ語の「計算」や「論理」といった意味合いから来ているのです。

数式で見るロジスティック曲線の仕組み

ここで少しだけ、実際の形を数式で見てみましょう。高校数学レベルの知識があれば大丈夫です。むしろ、この形を眺めるだけで「なるほど、だから上限があるのか」と納得できるはずです。

標準的なロジスティック関数（シグモイド関数）は、次のように表されます。

$f(x) = \frac{1}{1 + e^{-x}}$

ここで $e$ はネイピア数という特別な定数（およそ2.718）です。

$x$ は入力データ、例えば先ほどのウサギの話なら「時間」だと考えてください。

この式の分母に注目してみましょう。

$x$ がとても大きなプラスの数のとき： $e^{-x}$ は $0$ に限りなく近づきます。すると分母は $1 + 0$ になり、全体の結果は $1$ になります。これが「天井」です。
$x$ がとても小さなマイナスの数のとき： $e^{-x}$ はとてつもなく大きな数になります。分母が巨大になるので、全体の結果は $0$ に近づきます。これが「床」です。

つまり、どんなに大きな数字を入れても、どんなに小さな数字を入れても、答えは必ず $0$ と $1$ の間に収まるのです！

この「0から1の範囲に収まる」という性質が、確率を扱いたいエンジニアにとって非常に都合が良いのです。「ウサギが増えすぎて全滅する確率」や「このメールがスパムである確率」などを計算する際に、これ以上ないほど便利な道具となります。

ロジスティック曲線のメリットとデメリット

エンジニアとしてこの道具を使う際、良い点ばかりではありません。特徴をしっかり理解して使い分けることが大切です。

メリット

解釈が容易である出力が必ず $0$ から $1$ の間になるため、「確率」として直感的に理解できます。「出力が $0.8$ だから、80％の確率で成功する」といった説明がクライアントにしやすくなります。
計算コストが低いディープラーニングのような複雑な計算に比べ、計算式がシンプルです。そのため、大量のデータを高速に処理する必要があるシステムでも軽快に動作します。
微分の計算がきれいAIの学習（誤差逆伝播法など）では「微分」という計算を多用します。この関数の微分は、元の関数を使って非常にシンプルに書けるため、計算機にとって扱いやすいという隠れた利点があります。

デメリット

複雑な関係性を表現できないロジスティック回帰は、基本的には「直線を引いてデータを分ける」ようなシンプルな分類しかできません。データが複雑に入り組んでいる場合（例えば、ドーナツ型に分布しているデータなど）は、これ単体ではうまく分類できないことがあります。
極端な値に弱い場合がある入力データの中に、平均からかけ離れた異常な値（外れ値）があると、それに引きずられて分類の境界線がズレてしまうことがあります。

次のステップへ

いかがでしたか？

「ロジスティック」という名前が、トラックの物流ではなく、数学者の「現実的な上限を計算に入れたい」という知的探究心から来ていたとは、意外だったのではないでしょうか。

名前の由来を知ることは、その技術が生まれた背景や目的を理解することに繋がります。フェルフルストが「無限の増加」に疑問を持ったように、みなさんも「なぜこのアルゴリズムを使うのか？」と常に問いかけるエンジニアになってください。

さて、ロジスティック曲線を理解したあなたが次に学ぶべきは、これを応用したニューラルネットワークです。

実は、人間の脳を模したニューラルネットワークの細胞一つひとつの中で、このロジスティック曲線（シグモイド関数）が長年使われてきました。今日学んだ知識は、最先端のAI技術の基礎そのものなのです。

さあ、次は「ディープラーニング」の扉を叩いてみませんか？

準備ができたら、またいつでも声をかけてくださいね。

セイ・コンサルティング・グループの新人エンジニア研修のメニューへのリンク

投稿者プロフィール

山崎講師代表取締役

セイ・コンサルティング・グループ株式会社代表取締役。
岐阜県出身。
2000年創業、2004年会社設立。
IT企業向け人材育成研修歴業界歴20年以上。
すべての無駄を省いた費用対効果の高い「筋肉質」な研修を提供します！
この記事に間違い等ありましたらぜひお知らせください。