【脱・数学アレルギー】AIの基礎「シグモイド関数の微分」を高校生でもわかるように解説します

2026年1月24日 2026年1月24日山崎講師

山崎講師

こんにちは。ゆうせいです。

みなさんは、AIやディープラーニングの勉強をしていて、急に数式が出てきて手が止まってしまった経験はありませんか。特に「微分」という言葉を聞いただけで、少し身構えてしまう方もいるかもしれませんね。

でも、安心してください。実はAIが学習するために行っている計算は、仕組みさえわかってしまえば、それほど恐ろしいものではないのです。

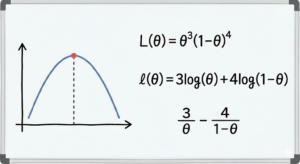
今回は、冒頭の画像にあるような問題を解くためのカギとなる「シグモイド関数の微分」について、専門用語を噛み砕きながらお話しします。なぜAIにこの関数が必要なのか、そして計算結果が何を意味するのか、一緒に紐解いていきましょう。

AIの「判断」をつかさどるシグモイド関数とは

まず、そもそもシグモイド関数とは何者なのでしょうか。

AI、つまりニューラルネットワークにおいて、入力されたデータを次の層へ伝える際に「活性化関数」というものが使われます。シグモイド関数は、その活性化関数の一種です。

少しイメージしにくいですよね。例え話をしましょう。

部屋の照明スイッチを想像してみてください。カチッと押すとオン、もう一度押すとオフになる普通のスイッチではなく、つまみを回すと徐々に明るくなったり暗くなったりする「調光スイッチ」をイメージしてください。

シグモイド関数は、まさにこの調光スイッチのような役割を果たします。入力された信号に対して、完全に無視する（0）でもなく、そのまま通す（1）でもなく、その間の「滑らかな数値」に変換して出力してくれるのです。

数式で書くと少し複雑に見えますが、形だけ眺めてみてください。

$f(z) = \frac{1}{1 + e^{-z}}$

この関数を通すと、どんなに大きな数字も小さな数字も、必ず $0$ から $1$ の間の数値に変換されます。これが、物事の確率（例えば、この画像が猫である確率は70パーセント、など）を表すのに非常に都合が良いのです。

なぜAI学習で「微分」が必要なのか

では、なぜこの関数を「微分」する必要があるのでしょうか。ここがAI学習のキモになります。

AIの学習とは、一言で言えば「間違い探しとその修正」の繰り返しです。AIが出した答えと、本当の正解との誤差を計算し、その誤差をできるだけ小さくするように、内部のパラメータ（重み）を調整していきます。

このとき、「パラメータを少し増やせば誤差が減るのか、それとも減らせば誤差が減るのか」を知る必要があります。

ここで登場するのが微分です。

微分とは、ある地点での「傾き」を求めることです。山登りに例えてみましょう。あなたは目隠しをして山の斜面に立っています。谷底（誤差がゼロの地点）に行きたいとき、足元の傾斜を感じ取って、下り坂の方向へ足を運びますよね。

この「足元の傾斜」を数学的に求める作業こそが、微分なのです。シグモイド関数を微分することで、AIは「どちらの方向に修正すれば賢くなれるか」を知ることができるのです。

シグモイド関数の微分の魔法

さて、ここからが本題です。シグモイド関数には、微分したときに現れる、とても美しい性質があります。

通常、分数の形をした関数の微分は計算が大変です。しかし、シグモイド関数 $f(z)$ を微分して導関数 $f'(z)$ を求めると、驚くほどシンプルな形になります。

$f'(z) = f(z) ( 1 - f(z) )$

見てください。微分した結果の中に、元の関数 $f(z)$ がそのまま使われているのがわかりますか。

これはプログラミングをする上で非常に大きなメリットになります。なぜなら、一度計算した $f(z)$ の値（高さ）さえわかっていれば、その値を使って簡単な掛け算をするだけで、瞬時に微分値（傾き）が求められるからです。複雑な計算をやり直す必要がありません。

「合成関数の微分」という武器

シグモイド関数の式を、少し見方を変えて書いてみましょう。分数の形ではなく、マイナス1乗の形として捉えます。

$f(z) = (1 + e^{-z})^{-1}$

こうすると、全体を「ある塊のマイナス1乗」として見ることができますね。ここで使うのが「合成関数の微分法（チェーンルール）」です。

イメージとしては、「外側の箱」を微分してから、その中にある「中身」を微分して掛け合わせる、という手順です。

手順1：外側を微分する

まず、 $(...)^{-1}$ の部分を微分します。

$x^n$ を微分すると $nx^{n-1}$ になるルールを思い出してください。

$-1 \times (1 + e^{-z})^{-2}$

手順2：中身を微分する

次に、カッコの中身である $1 + e^{-z}$ を微分します。

$1$ は定数なので消え、 $e^{-z}$ の微分は $-e^{-z}$ になります（ここでも合成関数の微分が使われています）。

$-e^{-z}$

手順3：合体させる

手順1と手順2を掛け合わせます。

$f'(z) = -1 \times (1 + e^{-z})^{-2} \times (-e^{-z})$

マイナスとマイナスを掛けるとプラスになるので、符号は消えますね。これをきれいに整理すると、以下のようになります。

$f'(z) = \frac{e^{-z}}{(1 + e^{-z})^2}$

これが、計算によって導き出された導関数です。

実際に問題を解いてみよう

それでは、冒頭の画像の問題に挑戦してみましょう。

問題：シグモイド関数 $Sigmoid(z) = f(z)$ が $z = 0$ をとる時、シグモイド関数の微分値 $f'(z)$ を求めなさい。ただし、 $Sigmoid(0) = f(0) = 0.5$ である。

先ほどの魔法の公式を使えば、もう怖くありませんね。

公式： $f'(z) = f(z) ( 1 - f(z) )$

ここでは $z = 0$ なので、 $f(0)$ の値を使います。問題文にある通り、その値は $0.5$ です。これを代入してみましょう。

式はこうなります。

$f'(0) = 0.5 \times ( 1 - 0.5 )$

カッコの中を計算すると $0.5$ ですね。つまり、

$f'(0) = 0.5 \times 0.5$

答えは、

$0.25$

となります。選択肢の「1」が正解です。

数学的な計算をしなくても、この「魔法の性質」さえ知っていれば、暗算でも解ける問題だったのです。

シグモイド関数のメリットとデメリット

最後に、シグモイド関数の良い点と、気をつけるべき点について整理しておきましょう。

メリット

出力が $0$ から $1$ の間に収まるため、確率として扱いやすい。
微分の計算が、元の関数の値を使って簡単にできるため、プログラムの負担が少ない。
自然界の現象や生物の神経活動に近い、滑らかな変化を表現できる。

デメリット

勾配消失問題（Vanishing Gradient Problem）が発生しやすい。

この「勾配消失問題」は少し難しい言葉ですが、今のうちに知っておくと役立ちます。

先ほどの計算で、微分値の最大が $0.25$ になることがわかりました。これは、層を深く重ねていくと、掛け算を繰り返すうちに値がどんどん小さくなってしまい、最終的に「ゼロ」に近づいてしまう現象です。

伝言ゲームで、列が長くなればなるほど、最初の言葉が後ろの人に伝わらなくなってしまうのに似ています。これにより、AIがうまく学習できなくなることがあるのです。

今後の学習の指針

いかがでしたか。

シグモイド関数の微分が、単なる数式の操作ではなく、AIが「賢くなるための方向」を探るための羅針盤であることを感じていただけたでしょうか。

0.25という数字も、ただの計算結果ではなく「シグモイド関数の傾きの最大値」として覚えると、より理解が深まります。

次は、このシグモイド関数の弱点である「勾配消失」を克服するために生まれた「ReLU（レル）関数」について学んでみると良いでしょう。現代のAI開発では、こちらが主役になることが多いです。

一歩ずつ、着実に理解を積み重ねていきましょう。応援しています！

次のステップ

「シグモイド関数」の形や、微分したときの「傾き」の変化を視覚的に確認できるPythonコード

import numpy as np
import matplotlib.pyplot as plt

# シグモイド関数の定義
def sigmoid(x):
    return 1 / (1 + np.exp(-x))

# シグモイド関数の微分の定義
# f'(x) = f(x) * (1 - f(x)) の公式を使用
def sigmoid_derivative(x):
    return sigmoid(x) * (1 - sigmoid(x))

# -10 から 10 まで、0.1 刻みのデータを作成
x = np.arange(-10, 10, 0.1)

# それぞれの計算結果を取得
y = sigmoid(x)
y_grad = sigmoid_derivative(x)

# グラフの描画設定
plt.figure(figsize=(8, 5)) # グラフのサイズ

# シグモイド関数の描画（青線）
plt.plot(x, y, label='Sigmoid f(z)')

# 微分の描画（オレンジの破線）
plt.plot(x, y_grad, linestyle='--', label="Derivative f'(z)")

# グラフの装飾
plt.title('Sigmoid Function and its Derivative')
plt.grid() # グリッド線を表示
plt.legend() # 凡例を表示
plt.xlabel('Input (z)')
plt.ylabel('Value')

# 画面に表示
plt.show()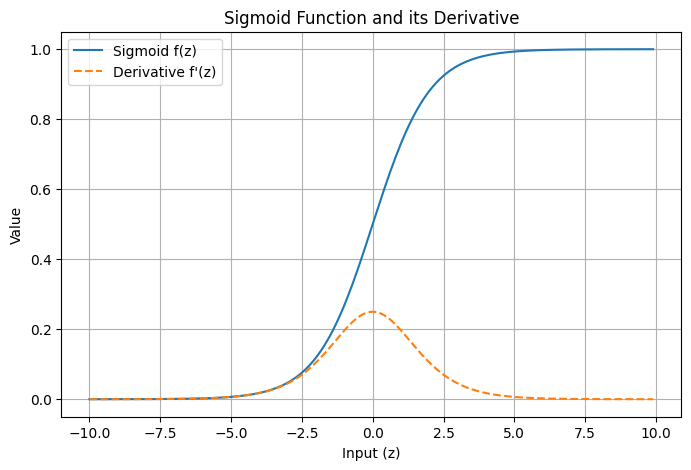

セイ・コンサルティング・グループの新人エンジニア研修のメニューへのリンク

投稿者プロフィール

山崎講師代表取締役

セイ・コンサルティング・グループ株式会社代表取締役。
岐阜県出身。
2000年創業、2004年会社設立。
IT企業向け人材育成研修歴業界歴20年以上。
すべての無駄を省いた費用対効果の高い「筋肉質」な研修を提供します！
この記事に間違い等ありましたらぜひお知らせください。

学生時代は趣味と実益を兼ねてリゾートバイトにいそしむ。長野県白馬村に始まり、志賀高原でのスキーインストラクター、沖縄石垣島、北海道トマム。高じてオーストラリアのゴールドコーストでツアーガイドなど。現在は野菜作りにはまっている。

【脱・数学アレルギー】AIの基礎「シグモイド関数の微分」を高校生でもわかるように解説します

AIの「判断」をつかさどるシグモイド関数とは

なぜAI学習で「微分」が必要なのか

シグモイド関数の微分の魔法

「合成関数の微分」という武器

手順1：外側を微分する

手順2：中身を微分する

手順3：合体させる

実際に問題を解いてみよう

シグモイド関数のメリットとデメリット

メリット

デメリット

今後の学習の指針

次のステップ

参考

セイ・コンサルティング・グループの新人エンジニア研修のメニューへのリンク

投稿者プロフィール

最新の投稿

PMOの仕事が整理される「3つの機能」とは？プロジェクトを成功に導く縁の下の力持ちNew!!

「識別モデル」と「識別関数」って同じじゃないの？新人エンジニアがハマる罠を解説New!!