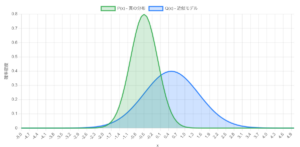
ソフトマックス関数の形ってどうしてあんな形なのか？

2026年2月6日 2026年2月6日山崎講師

山崎講師

こんにちは。ゆうせいです。

ディープラーニングの出力層で必ずと言っていいほど登場するソフトマックス関数。

分母にズラッと足し算が並んで、分子に指数関数が乗っているあの独特な姿を見て、「どうしてこんなに複雑なの？」と疑問に思うのは、とても自然で素晴らしい着眼点です！

実はあの形には、AIが「自信を持って答える」ための、とても合理的で賢い理由が隠されています。

なぜあの数式でなければならないのか、その秘密を解き明かしていきましょう。

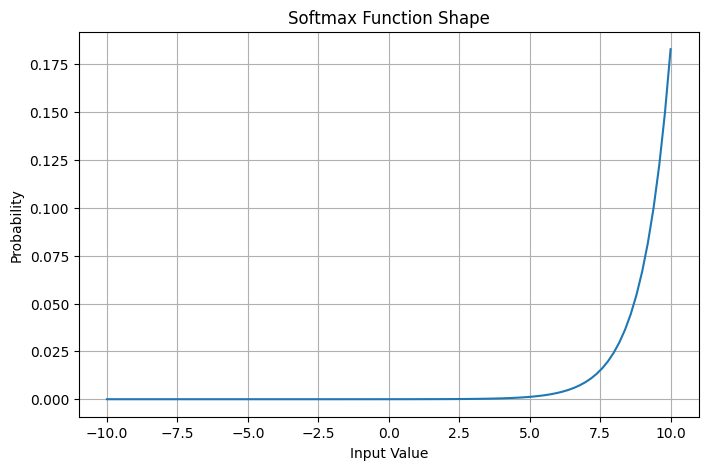
ソフトマックス関数の役割って？

まず、ソフトマックス関数が何をしているのかを、一言で表すと「バラバラな数字を『確率』に変換する装置」です。

AIが計算した直後の数字（ロジットと言います）は、10だったり、-5だったり、バラバラな値を取ります。

これでは「どれくらい確信があるのか」が直感的に分かりません。

そこで、ソフトマックス関数の出番です。

ここで、重要な専門用語を解説します。

指数関数（ $e^x$ ）数学の定数 $e$ （約 2.718 ）を何乗かする関数です。この関数の最大の特徴は「どんな小さな差も大きく広げて、かつ必ずプラスの数字にする」という点にあります。
正規化（せいきか）合計が 1 （100%）になるように調整することです。これにより、複数の選択肢を確率として扱えるようになります。

ソフトマックス関数の基本の形

複数の選択肢（例えば、画像に写っているのが「犬」「猫」「鳥」のどれか）があるとき、それぞれの選択肢の「自信のなさ」を含んだスコアを $x$ とします。

このとき、ある特定の選択肢 $i$ 番目が正解である確率 $y_i$ を求める式は、次のようになります。

$y_i$ = $\exp$ ( $x_i$ ) $\div$ $\sum$ $\exp$ ( $x_j$ )

この式を初めて見ると、目が回ってしまうかもしれませんね。

でも大丈夫です。

まずは、ここで使われている数学の記号を高校生でもわかるように噛み砕いてみましょう。

$\exp$ (エキスポネンシャル)これは「指数関数」のことで、 $e$ （ネイピア数：約 2.718）を何乗するかを表します。どんなに小さな数字もプラスに変え、少しの差を大きく広げる「強調」の役割を持っています。
$\sum$ (シグマ)「全部足し合わせる」という合図です。分母にあるこの記号は、すべての選択肢のスコアを合計することを意味しています。

つまり、どういう計算なの？

この数式の構造は、実はたったの2ステップです。

ステップ1（分子）：自分のスコア $x_i$ を指数関数の魔法にかけて、プラスの大きな数字に変えます。
ステップ2（分母）：全選択肢のスコアを同じように魔法にかけて、全部を合計します。

「自分の魔法の数字」を「全員の魔法の数字の合計」で割り算しているだけなのです。

クラスの合計点の中で、自分の点数が何パーセントを占めているかを計算しているのと、考え方は全く同じですよ！

どうしてあの式なの？

ソフトマックス関数の形を、イメージで分解してみましょう。

分子： $\exp$ ( $x$ )まず、指数関数を使って、すべての数字を無理やりプラスの大きな数字に変えます。
分母： $\sum$ $\exp$ ( $x$ )プラスになった数字を全部足し合わせます。

これらを割り算の形にすることで、「全体のエネルギーのうち、その選択肢がどれだけのシェアを占めているか」を計算しているのです。

あの形を採用するメリットとデメリット

なぜ単純な割り算ではなく、わざわざ指数関数（ $e$ ）なんて使うのでしょうか。

メリット1：わずかな差を「自信」に変える

普通の割り算だと、10 と 11 の差はわずかですが、指数関数を通すと $e^{10}$ と $e^{11}$ では大きな開きが出ます。

これにより、一番大きな値を持つ選択肢を強調し、「これが正解だ！」とAIがハッキリ主張できるようになります。

メリット2：微分ができる（学習に不可欠）

ディープラーニングは「間違いを修正する」ために微分という計算を使います。

指数関数は微分しても形が綺麗に残るため、計算の相性が抜群に良いのです。

デメリット：計算が爆発することがある

指数関数は数字が大きくなりやすいため、元の数字が大きすぎるとコンピュータが計算しきれなくなる（オーバーフロー）ことがあります。

そのため、実装の現場では「一番大きな数字を引いてから計算する」といった工夫が凝らされています。

変換のイメージを比較してみよう

もし「犬・猫・鳥」のスコアが以下のような場合、ソフトマックスを通すとどうなるでしょうか。

項目	元のスコア（ロジット）	ソフトマックス後の確率
犬	2.0	約 70%
猫	1.0	約 25%
鳥	0.1	約 5%

合計が 1.0 (100%) になりつつ、一番高いスコアがグンと目立つようになっていますね！

まとめ：あの形は「AIの意志」を作るため

いかがでしたか？

ソフトマックス関数のあの形は、単なる思いつきではなく、計算のしやすさと「一番を際立たせる」という目的が見事に合体したデザインなのです。

指数関数を使って、マイナスの数字を消し、差を広げる。
全部を足したもので割ることで、合計を 1 に揃える。
確率として解釈できるので、人間にもAIにも扱いやすい。

さて、ここであなたに質問です。

もしあなたが「今日のランチ」をソフトマックス関数で決めるとしたら、一番高いスコア（ロジット）を叩き出しそうなメニューは何ですか？

そのメニューが他の選択肢をどれくらい突き放しているか、あの式を思い浮かべながら考えてみると面白いですよ！

今後の学習の指針

ソフトマックス関数が理解できたら、次は「交差エントロピー誤差（クロスエントロピー）」について調べてみてください。

ソフトマックスが出した「確率」と、実際の「正解」がどれくらいズレているかを測るための、最強のパートナーです。

この二つが組み合わさることで、AIは賢くなっていくのです。

セイ・コンサルティング・グループでは新人エンジニア研修のアシスタント講師を募集しています。

投稿者プロフィール

山崎講師代表取締役

セイ・コンサルティング・グループ株式会社代表取締役。
岐阜県出身。
2000年創業、2004年会社設立。
IT企業向け人材育成研修歴業界歴20年以上。
すべての無駄を省いた費用対効果の高い「筋肉質」な研修を提供します！
この記事に間違い等ありましたらぜひお知らせください。

学生時代は趣味と実益を兼ねてリゾートバイトにいそしむ。長野県白馬村に始まり、志賀高原でのスキーインストラクター、沖縄石垣島、北海道トマム。高じてオーストラリアのゴールドコーストでツアーガイドなど。現在は野菜作りにはまっている。