大数の法則
こんにちは。ゆうせいです。
今日は「大数の法則」についてお話しします。この言葉、数学や統計学を勉強していると耳にする機会が増えると思いますが、初めて聞くと「なんだか難しそう…」と感じるかもしれません。でも、大丈夫!一緒にゆっくり理解していきましょう。
大数の法則とは?
簡単に言うと、大数の法則は「たくさん繰り返し観測すると、平均が理論値(本来あるべき値)に近づいていく」という原理です。
例えば、コインを投げたときに表が出る確率は理論上 50% ですよね。でも、コインを1回だけ投げたら表が出るか裏が出るかは運次第です。でも、これを100回、1000回、あるいはそれ以上繰り返すと、だんだんと表が出る割合が 50% に近づいていきます。この「たくさん繰り返すことで理論値に近づく」という現象が、大数の法則の本質なんです。
日常生活での例え
わかりやすい例として、「サイコロを振る」を考えてみましょう。
- サイコロには1から6の数字があります。
- それぞれの目が出る確率は 1/6(約16.7%) です。
- しかし、1回だけ振った場合、1が出るかもしれませんし、6が出るかもしれません。確率通りにはならないことが多いですよね。
でも、100回、1000回と振るとどうなるでしょう?すべての目が出た回数を数えてみると、それぞれの目が出る割合がほぼ 16.7% に近づくはずです。これがまさに大数の法則の効果です。
専門的な定義
もう少し専門的な言葉を使ってみましょう。
「確率変数の独立な試行を多数繰り返すとき、その標本平均は母平均に収束する」というのが数学的な定義です。
ここで登場する専門用語について解説します:
- 確率変数:何らかの試行(例:コイン投げ、サイコロ振り)によって結果が変わる値のこと。
- 標本平均:試行結果を合計して回数で割ったもの。つまり、たくさん試したときの平均値。
- 母平均:理論的に期待される真の平均値(例:コインの表が出る確率の50%)。
これを数式で表すと、次のようになります。
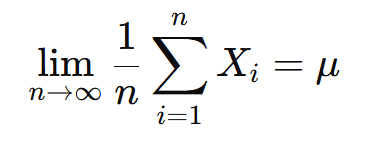
ここでの記号の意味は以下の通りです:

日本語で書き直すと、
「試行回数 ( n ) を無限に増やしたときに、試行結果の平均が母平均に収束する」となります。
メリットと限界
メリット
- データ分析の基礎:大数の法則は、統計学や確率論の基本的な考え方です。データが増えるほど正確な結論が得られるという安心感があります。
- 予測がしやすい:確率をもとにした予測が信頼できる理由を説明してくれます。
限界
- 小さなサンプルには適用できない:試行回数が少ないと、大数の法則は機能しません。例えば、コインを2回だけ投げて表が2回出ても、確率が100%とは言えませんよね。
- 独立した試行が条件:試行が独立でなければ成立しません。例えば、偏ったコインだと理論値には近づきません。
まとめと今後の学習
大数の法則は「たくさん試すと理論通りになる」というシンプルなルールですが、統計や確率の世界では非常に重要な役割を果たします。この考え方を知ることで、データ分析やゲームの確率の裏側にある法則を深く理解できるようになります。
今後は、この法則がどのように「確率分布」や「統計推定」とつながるのかを学んでみるといいですよ!また、ベイズ統計や統計的仮説検定といった応用分野にも目を向けると面白い発見があるはずです。
ぜひ挑戦してみてくださいね!
投稿者プロフィール

- 代表取締役
-
セイ・コンサルティング・グループ株式会社代表取締役。
岐阜県出身。
2000年創業、2004年会社設立。
IT企業向け人材育成研修歴業界歴20年以上。
すべての無駄を省いた費用対効果の高い「筋肉質」な研修を提供します!
この記事に間違い等ありましたらぜひお知らせください。
学生時代は趣味と実益を兼ねてリゾートバイトにいそしむ。長野県白馬村に始まり、志賀高原でのスキーインストラクター、沖縄石垣島、北海道トマム。高じてオーストラリアのゴールドコーストでツアーガイドなど。現在は野菜作りにはまっている。

