確率の謎を解く鍵！尤度関数をコイン投げで直感的に理解しよう

こんにちは。ゆうせいです。

みなさんは、手元にあるデータから「本当の確率」を推測したいと思ったことはありませんか。たとえば、コインを数回投げただけで、そのコインがイカサマかどうかなんてわかるのでしょうか。

実は、統計学にはそんな名探偵のような推理をするための便利な道具があるのです。それが今回紹介する尤度関数（ゆうどかんすう）です。

名前だけ聞くと「なんだか難しそう」と身構えてしまうかもしれませんね。でも大丈夫です。高校生のみなさんでもわかるように、コイン投げというシンプルな例を使って、その仕組みを紐解いていきましょう。

一緒に統計の不思議な世界を覗いてみませんか！

尤度関数ってなに？「確率」との違い

まずは言葉の意味から整理しましょう。尤度（ゆうど）という漢字、普段は見かけないですよね。これは「もっともらしさ」という意味を持っています。

確率と尤度は、実は見ている方向が逆なのです。

• 確率：コインの性質（表が出る確率）が決まっているときに、どんな結果が出るかを予想する
• 尤度：実際に起きた結果（データ）から、コインの性質（表が出る確率）を推理する

つまり、尤度関数とは「すでに起きた結果から逆算して、その原因となった確率のあてはまり具合を表す式」のことなのです。

コイン投げで式を作ってみよう

では、実際に式を作ってみましょう。ここからは少しだけ数学の記号を使いますが、安心してくださいね。

コインを投げたときに表が出る確率を、ギリシャ文字のテータを使って と置くことにします。

もしコインが完璧に平等なら は ですが、少し歪んでいたら かもしれません。この が正体不明の犯人です。

表が出る確率が なら、裏が出る確率はどうなるでしょうか。全体である から表の確率を引けばいいので、裏が出る確率は となりますよね。

具体的なケースで考える

ここで、ある実験をしてみましょう。コインを7回投げてみたところ、次のような結果になったとします。

「表、裏、裏、表、裏、裏、表」

この結果が得られる確率は、どのように計算すればよいでしょうか。

コイン投げの結果はお互いに影響を与えません。1回目に表が出たからといって、2回目に裏が出やすくなるわけではないですよね。このように独立している事象が連続して起こる確率を求めるときは、それぞれの確率を「掛け算」します。

実際に式に当てはめてみましょう。

1. 1回目（表）：
2. 2回目（裏）：
3. 3回目（裏）：
4. 4回目（表）：
5. 5回目（裏）：
6. 6回目（裏）：
7. 7回目（表）：

これらをすべて掛け合わせると、その瞬間の「もっともらしさ」を計算できます。

長い式になりましたね。でも、よく見てください。同じものがいくつかありませんか。

表（ ）は合計で3回出ています。

裏（ ）は合計で4回出ています。

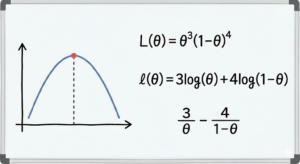
これを指数の形、つまり「◯◯の何乗」という形に整理してみましょう。そうすると、とてもスッキリした形になります。

これこそが、今回のデータにおける「尤度関数」です！

もし表が5回、裏が2回なら になりますし、表が2回、裏が5回なら になります。回数を数えて、それぞれの肩に乗せるだけ。意外と簡単だと思いませんか。

この に実際に具体的な数字を代入して、どの確率が一番「もっともらしい」のかを計算で確かめてみましょう。電卓を叩くような感覚で、気軽に付き合ってくださいね。

計算してみる

このコインの正体（表が出る本当の確率 ）として、3つの可能性を考えてみます。

1. 普通のコイン説（ ） なんの変哲もない、公平なコインだと仮定する場合です。
2. 裏が出やすいコイン説（ ） かなり歪んでいて、めったに表が出ないコインだと仮定する場合です。
3. データ通りのコイン説（ ） 今回の結果（7回中3回が表）をそのまま信じて、確率は約 だと仮定する場合です。

さあ、この3つのうち、どの説が今回の「表3回、裏4回」という結果を一番うまく説明できるでしょうか。計算してみましょう。

実際に計算してみよう

1. 普通のコイン説（ ）の場合

まずは、よくある普通のコインだった場合です。先ほどの式の に を入れます。

これを計算すると、

「約 」という数値が出ました。これが、普通のコインで今回の結果が出る「もっともらしさ」のスコアです。この数字が大きいほど、その説は有力だということになります。

2. 裏が出やすいコイン説（ ）の場合

次は、ちょっと極端な説を検証します。表が出る確率が （20%）しかない場合です。

カッコの中は になりますね。

「約 」となりました。 さっきの普通のコイン（ ）と比べると、スコアが半分以下になっています。つまり、「表が20%しか出ないコインで、今回のような結果になることは考えにくい」ということが数字で示されました。

3. データ通りのコイン説（ ）の場合

最後に、今回の実験結果（7回中3回が表、つまり で約 ）を確率として採用してみましょう。

少し計算が細かいですが、やってみます。

「約 」になりました。

結果を比べてみよう

3人の候補者のスコアが出揃いました。並べてみましょう。

• 普通のコイン（0.5）：
• 裏好きコイン（0.2）：
• データ通り（0.43）：

いかがでしょうか。 「データ通り」の と仮定したときが、一番スコアが高くなりましたね。普通のコイン（ ）も惜しかったのですが、今回は裏が少し多く出ている分、確率は より少し低いと考えるほうが自然だ、という結論になります。

このように、尤度関数の値が最大になる確率を探し出すことを、専門用語で「最尤推定（さいゆうすいてい）」と呼びます。「最も尤（もっと）もらしい値を推測する」という意味です。漢字の通りですね。

尤度関数を使うメリットとデメリット

この考え方は統計学において非常に重要ですが、もちろん良い点もあれば注意すべき点もあります。

メリット

最大のメリットは、客観的に「もっともらしい値」を決められることです。

先ほどの式 の値を最大にする を計算で求めれば、「このデータから考えると、表が出る確率はこれくらいだと考えるのが一番自然だ」という数値を誰でも同じように導き出せます。これを「最尤推定」と呼びます。

デメリット

一方で、データ数が少ないと極端な結果になりやすいという弱点があります。

たとえば、たまたまコインを3回投げて3回とも表が出たとしましょう。尤度関数だけで判断すると「このコインは100%表が出る魔法のコインだ！」という結論になってしまいます。常識的に考えればそんなことはないはずですが、計算上はそうなってしまうのです。

また、計算が複雑になりやすいという点も挙げられます。今回は掛け算だけで済みましたが、データが増えると数値が限りなくゼロに近づいてしまい、コンピュータでも扱いにくくなります。

次のステップへ

いかがでしたか。尤度関数という難しそうな言葉も、コイン投げの掛け算だと考えれば、ぐっと身近に感じられたのではないでしょうか。

データという「結果」から、確率という「原因」を探る。この探偵のようなプロセスこそが、統計学の醍醐味なのです。

ここからさらに学びを深めたい方は、ぜひ「対数尤度（たいすうゆうど）」について調べてみてください。先ほどデメリットで触れた「計算のしにくさ」を解消するために、掛け算を足し算に変換する魔法のようなテクニックです。

数学の力を使って、目の前のデータの裏側に隠された真実を解き明かしていきましょう！

セイ・コンサルティング・グループでは新人エンジニア研修のアシスタント講師を募集しています。

投稿者プロフィール

山崎講師代表取締役

セイ・コンサルティング・グループ株式会社代表取締役。
岐阜県出身。
2000年創業、2004年会社設立。
IT企業向け人材育成研修歴業界歴20年以上。
すべての無駄を省いた費用対効果の高い「筋肉質」な研修を提供します！
この記事に間違い等ありましたらぜひお知らせください。

学生時代は趣味と実益を兼ねてリゾートバイトにいそしむ。長野県白馬村に始まり、志賀高原でのスキーインストラクター、沖縄石垣島、北海道トマム。高じてオーストラリアのゴールドコーストでツアーガイドなど。現在は野菜作りにはまっている。

最新の投稿

• 新人エンジニア研修講師2026年1月18日AIの学習効率を劇的に変える「歩幅」の秘密とは？勾配降下法と学習率減衰
• 新人エンジニア研修講師2026年1月18日コイン投げで理解するデータ分析の第一歩！最尤推定をゼロから解説
• 新人エンジニア研修講師2026年1月18日確率の謎を解く鍵！尤度関数をコイン投げで直感的に理解しよう
• 新人エンジニア研修講師2026年1月18日機械学習の難所「バイアス・バリアンス」を完全攻略！モデルの複雑さとの関係とは？