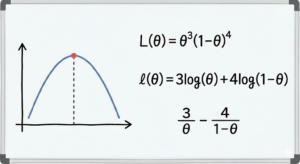
コイン投げで理解するデータ分析の第一歩！最尤推定をゼロから解説

2026年1月18日 2026年1月18日山崎講師

山崎講師

こんにちは。ゆうせいです。

突然ですが、あなたはコイン投げの結果を見て、そのコインがイカサマコインかどうか疑ったことはありますか？

たとえば、コインを 7 回投げて表、裏、裏、表、裏、裏、表という結果になったとしましょう。表が 3 回、裏が 4 回ですね。これだけだと、普通のコインのように見えます。でも、もし私たちがこの結果から、もっともありえそうな表が出る確率を計算できたら面白そうだと思いませんか？

今日は、そんな逆転の発想をする統計学の基礎、対数尤度関数（たいすうゆうどかんすう）について、一緒に学んでいきましょう。数学アレルギーの方も大丈夫です。ゆっくり紐解いていきますね！

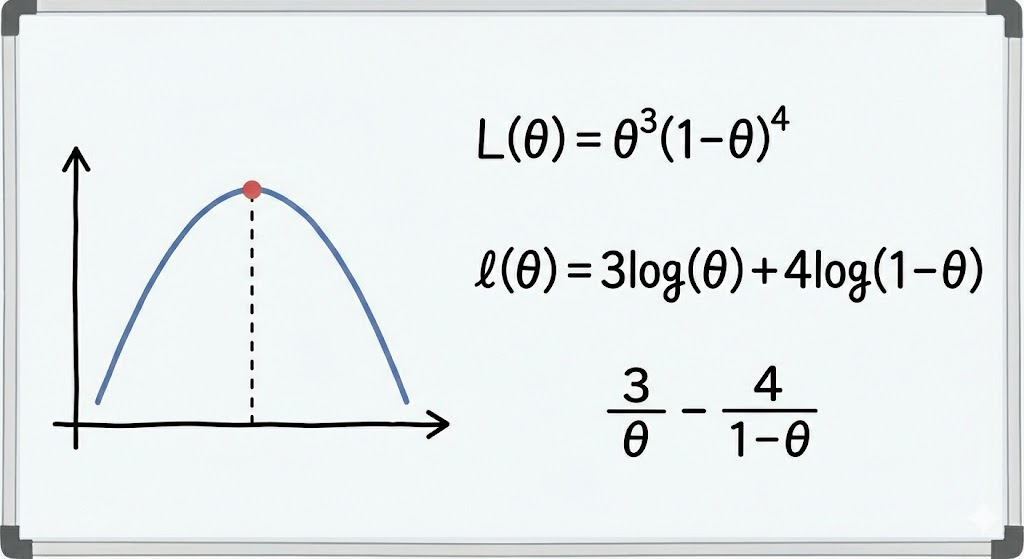
そもそも「尤度」ってなに？

まずは耳慣れない言葉、尤度（ゆうど）についてお話しします。これは英語で Likelihood（ライクリフッド）といい、もっともらしさを意味する言葉です。

普段、私たちは確率 $\theta$ （シータと読みます）が決まっている状態で、どんな結果が出るかを考えます。

しかし、現実の世界では結果（データ）が先に手に入り、その裏にある確率（仕組み）は未知であることが多いですよね。

この手元の結果から、原因である確率を推測しようというアプローチで使われるのが尤度です。つまり、得られたデータが起こる確率はどれくらいかを表す数式のことなんですよ。

コイン投げの問題を整理しよう

では、冒頭のコイン投げの問題を実際に考えてみましょう。状況はこうです。

コインを 7 回投げた
結果は表、裏、裏、表、裏、裏、表だった
表が出る確率を $\theta$ とする

ここで大切なのは、表が出た回数と裏が出た回数を数えることです。

結果を見ると、表は 3 回、裏は 4 回出ていますね。

表が出る確率は $\theta$ ですから、逆に裏が出る確率は全体の 1 から表の確率を引いて $1 - \theta$ となります。

尤度関数を作ってみよう

確率は、独立した試行（お互いに影響しない出来事）の場合、すべて掛け算するルールがあります。

今回の結果が起こる確率、つまり尤度 $L$ は次のように計算できます。

表が 3 回出る確率 $\times$ 裏が 4 回出る確率

これを数式にするとこうなります。

$L = \theta^3 \times (1 - \theta)^4$

これが尤度関数です！

でも、これだけだと掛け算がいっぱいで、計算するのがちょっと大変そうですよね？

そこで登場するのが、魔法の道具対数（ログ）です。

なぜ「対数」を使うの？

ここで今日の主役、対数尤度関数の登場です。

先ほどの尤度関数の頭に $\log$ （ログ）をつけたものを指します。

なぜわざわざ対数を取るのでしょうか？

実は、対数には掛け算を足し算に変えるという素晴らしい性質があるからです。

コンピュータで計算するとき、 $0.1 \times 0.1 \times 0.1 \dots$ と小さい数を掛け続けると、数字が小さくなりすぎて 0 になってしまうことがあります（これをアンダーフローといいます）。

しかし、対数を使って足し算に変換すれば、この問題を回避できる上に、計算自体もずっと楽になるんです。これが最大のメリットですね。

高校数学で習った、この公式を思い出してみましょう。

$\log(A \times B) = \log A + \log B$ （掛け算は足し算に！）
$\log(A^n) = n \log A$ （肩の荷（指数）を下ろせる！）

このルールを使うと、先ほどの式が劇的に変身しますよ。

問題の答えを導き出そう

では、尤度関数 $\theta^3 (1 - \theta)^4$ の対数をとってみましょう。

まず、掛け算を足し算に分解します。

$\log(\theta^3 \times (1 - \theta)^4) = \log(\theta^3) + \log((1 - \theta)^4)$

次に、指数の部分（肩に乗っている数字）を前に下ろします。

$3\log\theta + 4\log(1 - \theta)$

いかがですか？とてもスッキリした形になりましたね！

これが今回の問題の正解、つまり選択肢の 2 番となります。

$2\log\theta + 5\log(1 - \theta)$ （ハズレ：回数が逆ですね）
$3\log\theta + 4\log(1 - \theta)$ （正解！表3回、裏4回です）
$4\log\theta + 3\log(1 - \theta)$ （ハズレ：回数が逆転しています）
$5\log\theta + 2\log(1 - \theta)$ （ハズレ：回数が全然違います）

このように、対数尤度関数の係数（ログの前の数字）は、単純にその事象が起きた回数を表していると覚えると、直感的に理解しやすいですよ。

計算してみる

本当に「データから確率（ $\theta$ ）を逆算できるのか」を実験してみましょう。

ここでは、コンピュータでよく使われる自然対数（ $\log_e$ ）を使って計算した結果をお見せしますね。

ポイントは、この計算結果が「一番大きくなる数字」が、もっともらしい確率だということです。（対数はマイナスの値になることが多いので、0 に近いほうが「大きい」値ですよ！）

エントリーNo.1：普通のコイン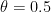（ $\theta = 0.5$ ）

まずは、誰もが思い浮かべる「普通のコイン」だった場合です。表が出る確率は 50% ですね。

数式： $3\log(0.5) + 4\log(1 - 0.5)$
計算： $3 \times (-0.693) + 4 \times (-0.693)$
結果： $-4.852$

まずはこの「マイナス4.852」というスコアを基準にしましょう。

エントリーNo.2：イカサマコイン（ $\theta = 0.1$ ）

次は、ほとんど表が出ないイカサマコインだった場合です。表が出る確率は 10% と仮定します。

実際のデータでは表が 3 回も出ているので、この確率は低そうですよね。計算で確認してみましょう。

数式： $3\log(0.1) + 4\log(1 - 0.1)$
計算： $3\log(0.1) + 4\log(0.9)$
計算： $3 \times (-2.302) + 4 \times (-0.105)$
結果： $-7.328$

スコアは「マイナス7.328」です。

さっきの「マイナス4.852」よりもだいぶ小さい（マイナスの幅が大きい）値になりました。つまり、尤度（もっともらしさ）が低いということですね。直感と合っています！

エントリーNo.3：データ通りの確率（ $\theta = 0.43$ ）

最後に、今回のデータ（7回中3回表）からそのまま計算した確率を試してみましょう。

$3 \div 7$ なので、約 43% （0.428...）です。これが一番もっともらしくなるはずですよね？

数式： $3\log(0.428) + 4\log(1 - 0.428)$
計算： $3\log(0.428) + 4\log(0.572)$
計算： $3 \times (-0.849) + 4 \times (-0.559)$
結果： $-4.782$

お待たせしました。スコアは「マイナス4.782」です！

結果発表

3つのスコアを並べてみましょう。

データ通りの確率（0.43）： $-4.782$ （優勝！）
普通のコイン（0.5）： $-4.852$
イカサマコイン（0.1）： $-7.328$

いかがでしょうか？

わずかな差に見えるかもしれませんが、 3/7（約0.43）のときに、値が最大（一番 0 に近い）になっていますね。

つまり、私たちが作った $3\log\theta + 4\log(1 - \theta)$ という関数は、適当な $\theta$ を入れると値が低くなり、最適な $\theta$ （今回は3/7）を入れたときに値が一番大きくなるようにできているのです。

微分して頂点を探せ

さて、いよいよ大詰めです。この関数の「頂点（最大値）」を見つけるにはどうすればよいでしょうか。

ここで登場するのが「微分（びぶん）」です。微分とは、グラフの傾きを調べる道具のこと。山の頂上では傾きがゼロになりますよね。つまり、微分してゼロになる場所を探せば、そこが答え（最大の尤もらしさ）になるわけです。

では、 $\theta$ について偏微分（へんびぶん）していきましょう。公式を使えば簡単です。

$\log(\theta)$ を微分すると $\frac{1}{\theta}$ になります。

これを使って、項ごとに計算してみますよ。

前半部分の微分

$3 \log(\theta)$ の部分は、単純に係数の3が残るので、次のようになります。

$\frac{3}{\theta}$

後半部分の微分（ここに注意！）

$4 \log(1 - \theta)$ の部分はどうでしょうか。ここには少し罠があります。「合成関数の微分」というルールが必要なんです。

まず外側の $\log$ を微分して $\frac{4}{1 - \theta}$ となりますが、これだけでは終わりません。中身の $(1 - \theta)$ を微分した $-1$ を掛け合わせる必要があります。

つまり、計算の流れはこうです。

$4 \times \frac{1}{1 - \theta} \times (-1)$

これを整理すると、符号がマイナスになりますね。

$- \frac{4}{1 - \theta}$

最終的な式の完成

前半と後半を合体させましょう。

$\frac{3}{\theta} - \frac{4}{1 - \theta}$

これが、対数尤度関数を $\theta$ で偏微分した結果です。

この式は、直感的に言うと「表の回数（3回）を確率で割ったもの」から「裏の回数（4回）を裏の確率で割ったもの」を引く形になっています。とても美しい構造だと思いませんか？

この式がゼロになる $\theta$ を求めれば、それが最も尤もらしい確率ということになります。

メリットとデメリットを知っておこう

対数尤度関数を使った分析（最尤推定法といいます）には、良い点もあれば注意すべき点もあります。

メリット

計算が簡単になる ：先ほど見た通り、複雑な掛け算をシンプルな足し算に変換できます。
どんな分布でも使える ：コイン投げだけでなく、身長の分布や故障率の予測など、あらゆるデータ分析の基礎として使えます。

デメリット

データが少ないと偏る ：例えばコインを 1 回投げて表が出たからといって、表が出る確率は 100% だ！と結論づけるのは早計ですよね？データ数が少ないと、極端な値が出やすくなります。
外れ値に弱い ：たまたま変なデータが混ざっていると、結果が大きく引っ張られることがあります。

今後の学習の指針

今日解説した対数尤度関数は、AIや機械学習の根幹を支える非常に重要な概念です。

ここからさらに学びを深めるために、次は以下のようなテーマに進んでみてはいかがでしょうか？

確率分布の種類を知る ：今回はコイン投げ（ベルヌーイ分布）でしたが、正規分布やポアソン分布など、世の中には色々な確率の形があります。

データを見る目が変わると、世界がもっと面白く見えてきますよ。

焦らず、一つひとつ数式の意味を味わってみてくださいね。

それでは、またお会いしましょう！

セイ・コンサルティング・グループでは新人エンジニア研修のアシスタント講師を募集しています。

投稿者プロフィール