【新人エンジニア向け】連立方程式をプログラムのように解く！「逆行列」と「掃き出し法」

2025年12月30日 2025年12月30日山崎講師

山崎講師

こんにちは。ゆうせいです。

前回は、行列の計算における「行と列の出会い」について、その独特な掛け算ルールをマスターしました。

今回は、いよいよ行列がその真価を発揮する瞬間をお見せします。テーマは、ズバリ「連立方程式」です。

中学校で習った $x$ や $y$ の連立方程式。

「上の式を2倍して、下の式から引いて……」と、一生懸命計算した思い出がありませんか？

変数が2つならまだしも、3つ、4つと増えていくと、手計算では限界が来ます。

しかし、行列の力を使えば、どんなに複雑な連立方程式も「たった一つのシンプルな式」で表現し、システマチックに解くことができるのです。

今回は、まるでパズルを解くような爽快感がある「掃き出し法」と、行列の世界での割り算にあたる「逆行列」について解説します。

連立方程式を「変形」するとは？

まず、具体的な連立方程式を例に考えてみましょう。

$\begin{cases} x_{1} + 4x_{2} = 7 \ 2x_{1} + 6x_{2} = 10 \end{cases}$

これを解くとき、皆さんは無意識に次のような操作をしているはずです。

「下の式から、上の式の2倍を引こう」と考えて、 $x_{1}$ を消す。
残った $x_{2}$ の式を整理する。
求まった $x_{2}$ を上の式に代入して $x_{1}$ を求める。

この一連の操作、実は「行列に対する変形」として書き換えることができます。

係数だけを取り出した行列を見てみましょう。

$\begin{pmatrix} 1 & 4 \ 2 & 6 \end{pmatrix}$

これに対して、「2行目から1行目の2倍を引く」といった操作を行い、最終的にシンプルな形（答えがすぐわかる形）に変形していく。これが「行基本変形（ぎょうきほんへんけい）」と呼ばれるテクニックです。

行基本変形の3つのルール

操作は難しくありません。使える魔法は次の3つだけです。

ある行を何倍かする（例：2行目を $\frac{1}{2}$ 倍する）。
ある行に、別の行の何倍かを加える（例：2行目に1行目の $-2$ 倍を加える）。
行と行を入れ替える。

この操作を繰り返して、最終的に次のような形を目指します。

$\begin{cases} x_{1} \quad \quad = \text{?} \ \quad \quad x_{2} = \text{?} \end{cases}$

つまり、係数の行列が次の形になればゴールです。

$\begin{pmatrix} 1 & 0 \ 0 & 1 \end{pmatrix}$

この形になったとき、右辺の数字がそのまま答えになります。

行列の世界の「1」と「割り算」

さて、ここで登場した $\begin{pmatrix} 1 & 0 \ 0 & 1 \end{pmatrix}$ という行列。

左上から右下への対角線上に $1$ が並び、それ以外が $0$ であるこの行列を、「単位行列（たんいぎょうれつ）」と呼びます 5。

単位行列 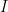$I$

これは、数の世界でいう「1」と同じ役割を持ちます。

$5 \times 1 = 5$ であるように、どんな行列 $A$ に単位行列 $I$ を掛けても、元の $A$ のまま変化しません。

逆行列 $A^{-1}$

では、数の世界でいう「逆数（割り算）」はあるのでしょうか？

$5 \times \frac{1}{5} = 1$ のように、ある行列 $A$ に掛け合わせると、答えが単位行列 $I$ （つまり1）になるような行列。

それを「逆行列（ぎゃくぎょうれつ）」と呼び、 $A^{-1}$ と書きます。

これがあると何が嬉しいのでしょうか？

連立方程式を行列で書いた式 $A \vec{x} = \vec{b}$ を思い出してください。

もし $A$ の逆行列 $A^{-1}$ がわかっていれば、両辺に左から $A^{-1}$ を掛けるだけで一発で答えが出ます。

$A^{-1} A \vec{x} = A^{-1} \vec{b}$

$I \vec{x} = A^{-1} \vec{b}$

$\vec{x} = A^{-1} \vec{b}$

つまり、「逆行列を求めること」＝「連立方程式を解くこと」なのです。

逆行列を求めるアルゴリズム「掃き出し法」

では、その便利な逆行列はどうやって求めればいいのでしょうか？

ここで登場するのが「掃き出し法（はきだしほう）」です。

これは、先ほどの「行基本変形」を使った賢い手順です。

言葉で説明するより、配置を見ると一目瞭然です。

元の行列 $A$ の隣に、単位行列 $I$ を並べて書きます。

$\left( \begin{array}{cc|cc} 1 & 4 & 1 & 0 \ 2 & 6 & 0 & 1 \end{array} \right)$

そして、左側の行列が単位行列になるように、行基本変形を行っていきます。

すると不思議なことに、同じ操作を右側の単位行列にも適用すると、最終的に右側に現れるのが逆行列 $A^{-1}$ なのです。

やってみよう

左側を変形する：左下の $2$ を消したいので、1行目を $-2$ 倍して2行目に足します 12。 $\left( \begin{array}{cc|cc} 1 & 4 & 1 & 0 \ 0 & -2 & -2 & 1 \end{array} \right)$
さらに変形：2行目を $-1/2$ 倍してシンプルにします。 $\left( \begin{array}{cc|cc} 1 & 4 & 1 & 0 \ 0 & 1 & 1 & -0.5 \end{array} \right)$
仕上げ：右上の $4$ を消したいので、2行目を $-4$ 倍して1行目に足します。 $\left( \begin{array}{cc|cc} 1 & 0 & -3 & 2 \ 0 & 1 & 1 & -0.5 \end{array} \right)$

これで左側が単位行列になりました。

このとき、右側にできあがった $\begin{pmatrix} -3 & 2 \ 1 & -0.5 \end{pmatrix}$ こそが、求めていた逆行列です！

今回のまとめ

今回は、連立方程式を行列の力で解く方法について解説しました。

行基本変形 ：式を足したり引いたりする操作を行列上で行うこと。
単位行列 $I$ ：掛け算しても相手を変えない、行列界の「1」。
逆行列 $A^{-1}$ ：行列界の「割り算」。掛けると単位行列になる。
掃き出し法 ：行基本変形を使って、機械的に逆行列を求めるアルゴリズム。

一見複雑に見える連立方程式も、この手順（アルゴリズム）に従えば、コンピュータを使って一瞬で解くことができます。これが、プログラミングやデータ解析で行列が重宝される理由の一つです。

しかし、世の中には「どうしても解けない連立方程式」や「逆行列が存在しない行列」も存在します。

「逆数が存在しない数」なんてあるの？と思うかもしれませんが、 $0$ で割ることができないのを思い出してください。

次回は、そんな特異なケースを見極めるための重要な指標、「行列式（ぎょうれつしき）」について解説します。

「面積」の概念を使うと、行列の性質が手に取るようにわかりますよ。

それでは、また次回お会いしましょう！

セイ・コンサルティング・グループの新人エンジニア研修のメニューへのリンク

投稿者プロフィール

山崎講師代表取締役

セイ・コンサルティング・グループ株式会社代表取締役。
岐阜県出身。
2000年創業、2004年会社設立。
IT企業向け人材育成研修歴業界歴20年以上。
すべての無駄を省いた費用対効果の高い「筋肉質」な研修を提供します！
この記事に間違い等ありましたらぜひお知らせください。

学生時代は趣味と実益を兼ねてリゾートバイトにいそしむ。長野県白馬村に始まり、志賀高原でのスキーインストラクター、沖縄石垣島、北海道トマム。高じてオーストラリアのゴールドコーストでツアーガイドなど。現在は野菜作りにはまっている。