【保存版】暗記不要！エンジニアの視点で読み解く「ネイピア数の公式」厳選ガイド

2026年1月13日 2026年1月13日山崎講師

山崎講師

こんにちは。ゆうせいです。

前回は、機械学習の世界で「ネイピア数 $e$ 」がいかに愛されているか、その理由を熱く語らせていただきました。

「便利なのはわかったけど、実際どんな式で使うの？」

「教科書に出てくる公式が多すぎて、どれを覚えればいいのかわからない……」

そんな声が聞こえてきそうです。わかります、その気持ち。数学の公式集って、まるで呪文のリストみたいに見えますよね。

でも、安心してください。エンジニアとして現場で戦うために必要なネイピア数の知識は、実はごく一部なんです。すべてを丸暗記する必要はありません。

きょうは、数ある公式の中から「これだけ知っていればエンジニアとして会話ができる」という、本当に使える公式だけを厳選しました。それぞれの数式が持つ「意味」や「物語」と一緒に紹介しますので、読み物として楽しんでくださいね。

1. ネイピア数の正体を表す「定義の式」

まずは、そもそも $e$ とはどうやって生まれたのかを表す式です。

$e = \lim_{n \to \infty} (1 + \frac{1}{n})^n$

うっ、いきなり難しそうな記号が出てきた……と身構えないでください！

この式は、実は「成長の限界」というとてもシンプルな物語を語っているんです。

高校生にもわかる解説

この式は「銀行の金利」で考えると一発でわかります。

想像してみてください。元金が $1$ 万円あるとします。年利 $100$ ％という夢のような銀行があったとしましょう。

$1$ 年後に受け取ると $2$ 万円になりますね。では、半年に一回、利息を受け取って再投資したら？毎日利息を受け取ったら？一秒ごとに受け取ったら？

回数を増やせば増やすほど、お金は無限に増えていく気がしますよね。

しかし、この式にある $\lim$ （リミット）は、こう告げているんです。

「どれだけ細かく分割して成長させても、ある一定の数字以上には増えないよ」

その「成長の天井」こそが、ネイピア数 $e$ （約 $2.718$ ）なのです。この式を見たら、「ああ、無限の成長を追い求めた結果の数字なんだな」と思い出してください。

2. エンジニアが一番使う「無敵の微分公式」

次は、機械学習エンジニアにとっての最強の武器となる公式です。

$(e^x)' = e^x$

これは「 $e$ の $x$ 乗を微分しても、 $e$ の $x$ 乗のまま」という意味です。

なぜこれが凄いの？

他の数字で見てみましょう。たとえば $x$ の $2$ 乗を微分すると $2x$ になり、形が変わってしまいます。微分をするたびに、式はどんどん姿を変えていくのが普通です。

しかし、ネイピア数だけは違います。

何度微分しても、何度衝撃を与えても、元の姿を保ち続ける。まるで形状記憶合金のような、あるいは何度倒されても立ち上がるヒーローのような性質を持っています。

機械学習では、複雑な計算を何度も繰り返して「最適解」を探します。その計算過程で、微分しても形が変わらないという性質は、計算コストを劇的に下げてくれる「神機能」なのです。

この式を見たら、「計算をラクにしてくれる魔法の呪文」だと思って感謝しましょう！

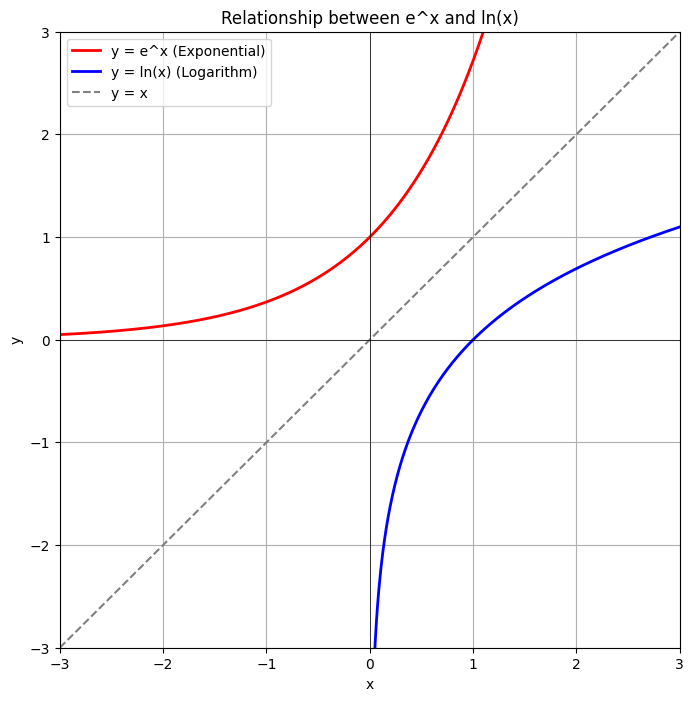
3. 確率・統計への架け橋「対数の公式」

続いては、 $e$ と切っても切れない関係にある「対数（ログ）」の公式です。

$\ln(e) = 1$

「 $\ln$ 」という記号を見て、アレルギー反応が出そうになったあなた。大丈夫です。これは単に「 $e$ を何乗したらその数になりますか？」という質問を記号にしただけです。

会話形式で翻訳すると

この式は、次のような会話を表しています。

質問者（ $\ln$ ）：「ねえねえ、 $e$ を何乗したら、カッコの中の数字（ $e$ ）になる？」
回答者：「え？ $e$ を $e$ にしたいんでしょ？それなら $1$ 乗すればいいだけじゃん」
結果：「だから答えは $1$ です」

当たり前のことを言っているように見えますが、これが非常に重要です。

機械学習では、掛け算を足し算に変換したり、非常に小さな確率を扱いやすい大きさに変換したりするために、この「対数」を頻繁に使います。

$e$ を基準（底）にした対数のことを「自然対数」と呼び、エンジニアの世界では標準語のように使われます。

4. 世界で最も美しい数式「オイラーの等式」

最後は、実用性というよりも「教養」として知っておきたい、数学界の至宝です。

$e^{i\pi} + 1 = 0$

ネイピア数（ $e$ ）：解析学の主役
円周率（ $\pi$ ）：幾何学の主役
虚数単位（ $i$ ）：代数学の主役
$1$ ：数の始まり
$0$ ：無

まったく別々の分野で生まれたスターたちが、一つの式の中で奇跡的な調和を見せているのです。

エンジニアとしての捉え方

直接的なコーディングでこの式を書くことは少ないかもしれません。しかし、信号処理や量子コンピュータの分野では、この式の考え方がベースになっています。

この式を見かけたら、「数学にも芸術のような美しさがあるんだな」と、ちょっと知的な気分に浸ってみてください。

まとめ：公式は「道具」であり「言葉」です

いかがでしたか？

ただの記号の羅列に見えていた公式たちも、その意味を知れば、少し親しみが湧いてきたのではないでしょうか。

成長の限界を知る定義式
変化しても変わらない微分の式
計算を翻訳する対数の式

これらはテストのために覚えるものではなく、エンジニアが問題を解決するための「道具」です。

今後の学習への指針

まずは、一番実用的な「 $(e^x)' = e^x$ 」という性質だけでも持ち帰ってください。

そして、次に技術書を読んでいて $e$ が出てきたら、読み飛ばさずに立ち止まってみてください。「お、ここで変化率が変わらない性質を利用しているのかな？」と推測できるようになれば、あなたはもう初心者を卒業しています。

さあ、恐れることはありません。ネイピア数という頼もしい相棒と一緒に、プログラミングの世界をもっと深く探求していきましょう！

セイ・コンサルティング・グループでは新人エンジニア研修のアシスタント講師を募集しています。

投稿者プロフィール

山崎講師代表取締役

セイ・コンサルティング・グループ株式会社代表取締役。
岐阜県出身。
2000年創業、2004年会社設立。
IT企業向け人材育成研修歴業界歴20年以上。
すべての無駄を省いた費用対効果の高い「筋肉質」な研修を提供します！
この記事に間違い等ありましたらぜひお知らせください。

学生時代は趣味と実益を兼ねてリゾートバイトにいそしむ。長野県白馬村に始まり、志賀高原でのスキーインストラクター、沖縄石垣島、北海道トマム。高じてオーストラリアのゴールドコーストでツアーガイドなど。現在は野菜作りにはまっている。