最小二乗法について

2024年11月9日 2024年11月9日山崎講師

山崎講師

こんにちは。ゆうせいです。

今日は「最小二乗法」についてお話ししますね。これも少し難しそうに聞こえるかもしれませんが、誰でもわかるように、例えを交えながらわかりやすく説明していきます。

最小二乗法とは何か？

最小二乗法（さいしょうにじょうほう）は、データの点に一番近い「最適な直線」を見つける方法です。具体的には、データのバラバラな点がどのように分布しているかに対して「この点たちをできるだけ近くに寄せて通る直線」を引き、その直線を使って予測をしたりします。

例えば、時間が経つと成績が上がるかもしれない、というデータがあったとします。ここで最小二乗法を使うと、「時間が増えるほど成績も増える」という関係が、具体的にどれくらいの傾きで伸びているかを示す直線が求められます。

例えで考える：散らかった点と直線

例えば、黒板にポンポンといくつかの点が書かれていて、これらの点にできるだけ近い直線を1本引いてみるとします。しかし、全ての点をピッタリと通る直線を引くのは難しい場合がほとんどです。なので、ピッタリ通らなくても、なるべく「全体的に近い位置にある直線」を見つけたいですよね。

ここで使えるのが「最小二乗法」です。この方法は、点と直線の「ずれ（誤差）」が最も小さくなるように計算して、理想的な直線を見つけ出すものです。

最小二乗法の計算方法

最小二乗法で直線を求めるには、次のような計算を行います。

数式で見る最小二乗法

最小二乗法で求める直線の方程式はこうです：

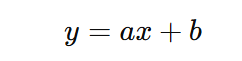
y ：縦軸（結果や予測したい数値）
x ：横軸（時間や測定した数値）
a ：直線の傾き
b ：直線の切片（y軸と交わるところ）

この傾き (a) と切片 (b) を計算するのが最小二乗法の目的です。

傾きと切片を求める数式

傾き ( a ) と切片 ( b ) の計算式は次の通りです：

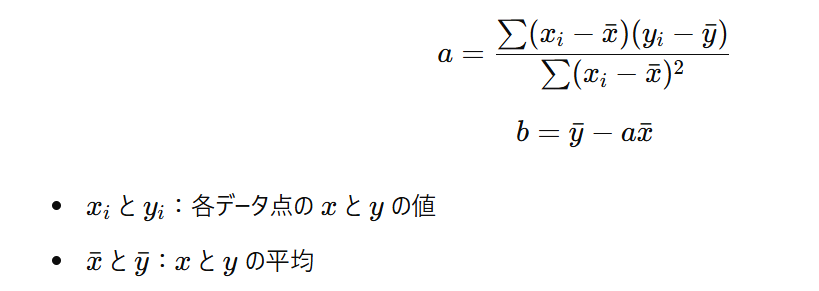
この数式を使うと、「データのばらつき」に最も適した直線の傾き (a) と切片 (b) を求めることができます。

最小二乗法の仕組みをかみ砕く

最小二乗法では、データ点と予測直線の「ずれ」が大きいと、そのずれを小さくしたいと考えます。そのため、各データ点と直線の距離を二乗して合計し、その合計が最も小さくなるような直線を求めるのです。二乗する理由は、プラスとマイナスのずれが相殺されずに、全てのずれを正の数として扱うためです。

例えば、ある点が直線よりも上にずれていれば、そのずれはプラスになります。一方、下にずれていればマイナスになります。こうしたずれを二乗すると、プラスもマイナスもどちらも正の数になるので、全体的なずれがわかりやすくなるのです。

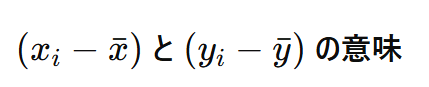
この式の中で出てくる分子の部分は、それぞれ「xやyのデータの各値から平均値を引いたもの」を表しています。

なぜ平均値を引くのか？

平均値を引く理由は、「各データがどれくらい離れているか」を見やすくするためです。平均からの差を見ることで、データが「どの方向（増える方向か減る方向か）」に「どれくらい動いているか」を把握しやすくなります。

たとえば、気温とアイスの売上データがあった場合、気温が平均より高いときに売上も平均より高ければ、気温と売上には「同じ方向に動く関係」があるとわかります。逆に、気温が平均より高いときに売上が平均より低ければ、「逆の方向に動く関係」があるとわかります。

分子部分の意味：

分子の部分は、「xとyがどれだけ一緒に増えたり減ったりするか」を計算しています。

xとyが同じ方向に動くとき（例えば、xが平均より大きいときにyも平均より大きい場合）、分子の値は正の数になります。
xとyが逆の方向に動くとき（例えば、xが平均より大きいときにyは平均より小さい場合）、この部分の値は負の数になります。

このように、xとyがどれくらい「一緒に動いているか」を示しているのが分子の部分です。

分母部分の意味は、「xのデータがどれくらいばらついているか」を表しています。これは「xのばらつき」を表す指標で、もしxがバラバラな値を取っているなら大きな数になりますし、xが同じような値を取っているなら小さな数になります。

この分母の値が大きいと、「xが増えたときのyの変化量」を求める際に影響を受けます。ばらつきが大きいとyの影響も減り、小さいとyへの影響が増えます。これは、xの変動がどれだけyに影響を与えるかを調整する役割をしています。

全体の意味

まとめると、傾きは、「xとyがどれだけ一緒に動いているか（分子）」を「xがどれだけ変動しているか（分母）」で割って、xの変動に対してyがどれくらい反応するかを示しています。この傾きが大きいと、xが増えるとyも大きく増え、小さいとyの増え方も小さくなるのです。

最小二乗法のメリットとデメリット

メリット

データの傾向がわかりやすくなり、予測に役立つ。
グラフを使うことで、どのような関係があるのか視覚的に把握しやすい。
数学的な根拠を持って、データから最適な直線を引ける。

デメリット

全てのデータにぴったり合うわけではないため、外れ値（極端にずれたデータ）があると直線が影響を受けやすい。
線形関係でないデータには適用しづらい（例えば、曲がったデータには最小二乗法ではなく、別の方法が必要）。

まとめと今後の学習

最小二乗法は、データに最も近い直線を引いて「全体の傾向をつかむ」ための便利な方法です。最小二乗法を学ぶことで、データの分析や予測がしやすくなり、数学や統計学の世界がさらに深く理解できるようになりますよ！次は、最小二乗法がどのように実際のデータに応用されるかや、非線形のデータに対応する他の方法について学んでみると良いでしょう。

投稿者プロフィール

山崎講師代表取締役

セイ・コンサルティング・グループ株式会社代表取締役。
岐阜県出身。
2000年創業、2004年会社設立。
IT企業向け人材育成研修歴業界歴20年以上。
すべての無駄を省いた費用対効果の高い「筋肉質」な研修を提供します！
この記事に間違い等ありましたらぜひお知らせください。