「ビュフォンの針の実験」のシミュレーター

2024年11月16日 2024年11月16日山崎講師

山崎講師

こんにちは。ゆうせいです。

今日は「ビュフォンの針の実験」についてお話しします。この実験は、数学や確率の面白さを実感できるだけでなく、円周率（π）を求めるという驚きの応用もあるんです！聞いたことがなくても大丈夫。わかりやすく説明していきますね。

ビュフォンの針の実験とは？

18世紀のフランスの数学者ジョルジュ＝ルイ・ルクレール・ド・ビュフォンが考案したこの実験は、確率を使って円周率（π）を求める方法です。一見、不思議に思えるかもしれませんが、「針を投げて、どれくらいの確率で床の線に触れるか」を調べる実験です。

まず簡単にイメージしてみましょう。

床に等間隔に引かれた平行線があります。
その上に長さが一定の針を何度も投げます。
投げた針が「線に触れる確率」と「円周率（π）」に関係があるんです！

「え、どういうこと？」と思いますよね。具体的に説明していきます。

実験の手順

この実験は次のように進めます。

1. 条件を整える

床に平行な線を引きます。この線の間隔を d とします。そして、針を用意します。この針の長さを l としましょう。

重要なのは、針の長さ l が線の間隔 d 以下であることです。つまり、針の長さが長すぎるとダメということですね。

2. 針を投げる

針を何度も無作為に投げます。無作為というのは、針がどの方向に向くか、どこに落ちるかが全くランダムになるようにすることです。

3. 線に触れるか確認する

針が線に触れるかどうかを記録します。

結果と円周率（π）の関係

針が線に触れる確率 P は次の公式で表されます。

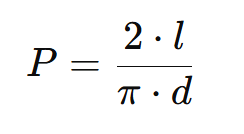
ここで、 π が登場しました！この公式を使うと、円周率を推定することができます。

確率から円周率を求める

確率の公式を変形してみましょう。円周率は次のように求められます。

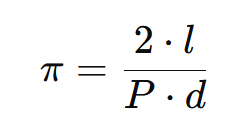
針をたくさん投げて、線に触れる回数を記録すれば確率 P がわかります。これを使って円周率を計算するのです。

例えば、1000回針を投げて、そのうち300回線に触れたとします。この場合、確率 P は

P = 300 / 1000 = 0.3

これを先ほどの公式に代入すると、円周率が計算できるのです！

なぜこんなことができるの？

この仕組みの裏には、幾何学と確率の密接な関係があります。針の角度や位置がランダムである場合、針の先端がどこに落ちるかの確率が幾何学的に解析できるためです。

イメージとしては、針を投げる動作が「ランダムな実験」の代表例となり、その結果が数学的な普遍性を示しているのです。

メリットと限界

メリット

円周率を実験で求めるという驚きの方法。
確率や幾何学の理解が深まる。

限界

精度が高くない。非常に多くの試行回数が必要。
実験条件（針の長さや線の間隔）が乱れると誤差が生じる。

まとめ

ビュフォンの針の実験は、確率や幾何学を体感する素晴らしい方法です。このシンプルな実験から、円周率という壮大な数学の概念に迫れるのは驚きですね。

もし興味が湧いたら、自分で試してみるのもおすすめです。床に線を引いて、針を投げるだけですから簡単ですよ！数学の面白さを、ぜひ体験してみてください。

今後は、この実験の背後にある確率論や幾何学の詳しい理論を学ぶのもいいでしょう！

「ビュフォンの針の実験」のシミュレーターへのリンク

投稿者プロフィール

山崎講師代表取締役

セイ・コンサルティング・グループ株式会社代表取締役。
岐阜県出身。
2000年創業、2004年会社設立。
IT企業向け人材育成研修歴業界歴20年以上。
すべての無駄を省いた費用対効果の高い「筋肉質」な研修を提供します！
この記事に間違い等ありましたらぜひお知らせください。