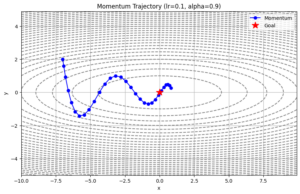
【研修講師向け】「慣性」を味方につける！Momentumを物理の実験のように教えるテクニック

2026年1月26日 2026年1月26日山崎講師

山崎講師

こんにちは。ゆうせいです。

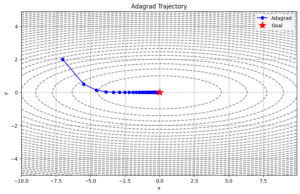
前回は、足元の状況に合わせて慎重さを変える「Adagrad（アダグラッド）」についてお話ししました。今回は、それとは対照的に、勢いよく坂道を駆け下りるアルゴリズム「Momentum（モーメンタム）」について解説します。

研修でこの単元に入ると、受講生からこんな声が上がることがあります。

「SGDと何が違うんですか？」

「数式の $\alpha$ （アルファ）って何の意味があるんですか？」

Momentum は、直訳すると「運動量」です。つまり、ここでの主役は「物理法則」です。

今日は、難解な数式を「坂道を転がるボール」の動きに置き換えて、誰でもイメージできる教え方をご紹介します。

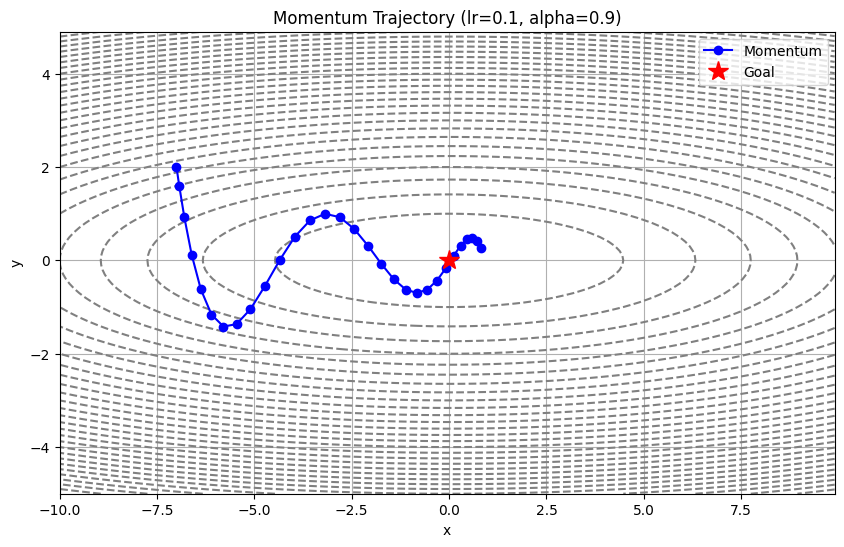
SGDの弱点と「ジグザグ運転」

まずは、基本となるSGD（確率的勾配降下法）の弱点を思い出してもらいましょう。

SGDは、現在の傾斜だけを見て進む方向を決めます。

これを人間に例えると、「足元の傾きしか見ていない、視野の狭い人」です。

谷底に向かう道がジグザグしている場合、SGDはどうなるでしょうか？

右の斜面で「左だ！」と向きを変え、左の斜面で「右だ！」と向きを変える。

あっちへフラフラ、こっちへフラフラ。これを繰り返して、なかなか谷底にたどり着けません。

ここで Momentum の登場です。

「フラフラするなら、重たい荷物を持たせて勢いをつけてしまえばいいじゃない」

これが Momentum の発想です。

ボウリングの球をイメージさせる

生徒さんには、こう問いかけてみてください。

「坂道で、ピンポン玉とボウリングの球を転がします。途中に小さなデコボコがあったとき、どちらがスムーズに進みますか？」

答えはもちろん、ボウリングの球です。

なぜなら、ボウリングの球には「重さ」があり、一度スピードに乗ると、多少のデコボコや横からの力に影響されずに、その「勢い（慣性）」で進み続けようとするからです。

Momentum というアルゴリズムは、パラメータの更新にこの「慣性」を取り入れたものです。

「前回のスピードを記憶しておいて、今回もその勢いを借りて進む」

こうすることで、ジグザグした道でも、過去の勢いが働き、滑らかに谷底へ滑り降りることができるのです。

数式とコードをつなぐ「空気抵抗」の話

では、Momentum の数式を見てみましょう。

先ほどの問題にもあった式です。

$v \leftarrow \alpha v - \eta \frac{\partial L}{\partial W}$

この式を、物理の言葉で翻訳してあげてください。

$v$ ： 現在のスピード（速度）
$- \eta \frac{\partial L}{\partial W}$ ： 今の坂道による加速（SGDと同じ部分）
$\alpha v$ ： ここが Momentum の本体！

$\alpha$ （アルファ）は、プログラムでは momentum という変数名でよく使われ、一般的に $0.9$ などの値が設定されます。

これは「摩擦」や「空気抵抗」と説明すると分かりやすいです。

「 $0.9$ を掛けるということは、前のスピードの $90$ ％を維持するということです。つまり、摩擦で $10$ ％だけ減速するけど、残りの勢いはそのまま使うよ、という意味なんです」

Pythonコードで見る Momentum の正体

それでは、実際のコードを見てみましょう。

「速度」を保存する変数が必要になる点に注目させてください。

以下のコードは、研修でそのまま使えるサンプルです。

import numpy as np

class Momentum:
    def __init__(self, lr=0.01, momentum=0.9):
        self.lr = lr              # 学習率（eta）
        self.momentum = momentum  # 慣性の強さ（alpha）
        self.v = None             # 速度の記憶（初期値はNone）

    def update(self, params, grads):
        # 初回のみ速度 v を初期化（0で埋め尽くされた辞書を作る）
        # 最初は止まっているので速度は0です
        if self.v is None:
            self.v = {}
            for key, val in params.items():
                self.v[key] = np.zeros_like(val)

        for key in params.keys():
            # 【ここがポイント】
            # 新しい速度 = (前の速度 × 0.9) - (今の傾き × 学習率)
            # 勢いを保ちつつ、坂道の傾斜で加速・減速します
            self.v[key] = self.momentum * self.v[key] - self.lr * grads[key]

            # パラメータの位置を更新
            # 現在地から、計算した速度の分だけ移動します
            params[key] += self.v[key]

講師としての解説ポイント

コードを見せながら、SGDとの決定的な違いを伝えてください。

変数 v があるSGDには「現在地」しかありませんが、Momentumには「速度（v）」という概念があります。
self.momentum * self.v[key]ここが「慣性」です。過去の自分がどれくらいのスピードで走っていたかを計算に入れています。もし坂道の傾き（grads）が突然 $0$ （平坦）になっても、この項があるおかげで、ボールはすぐに止まらずに転がり続けます。これが「学習が停滞しにくい」というメリットに繋がります。

Momentum のメリットとデメリット

最後に、この手法の特徴をまとめて、生徒さんの理解を整理しましょう。

メリット

ジグザグを抑える: 慣性が働くので、横方向への細かい振動を無視して、谷底へ一直線に向かいやすくなります。
局所解（ローカルミニマ）に強い: 小さな窪み（ニセのゴール）にハマっても、勢いがあるので「おっとっと」と乗り越えて脱出できることがあります。

デメリット

行き過ぎる（オーバーシュート）: 勢いがつきすぎて、本当のゴール（谷底）を通り過ぎてしまい、行ったり来たりすることがあります。
- 「ボウリングの球は急には止まれないですよね？」と補足してあげてください。

今日のまとめ

いかがでしたか？

Momentum は「重たいボウリングの球」
数式の $\alpha v$ は「前の勢いを維持する力（慣性）」
ジグザグ運転を抑えてスムーズに進むが、勢い余って行き過ぎることもある

「SGDは徒歩、Momentumは自転車」のような乗り物の例えも有効です。

こうしてアルゴリズムに「動きのイメージ」を持たせることで、無機質な数式が生きた知識に変わります。

次回は、今回学んだ「Momentum（慣性）」と、前回学んだ「Adagrad（足元の調整）」を合体させた、現在最強と言われるアルゴリズム「Adam」について解説します。いよいよラスボスの登場です！

それでは、また次の記事でお会いしましょう。

セイ・コンサルティング・グループでは新人エンジニア研修のアシスタント講師を募集しています。

投稿者プロフィール

山崎講師代表取締役

セイ・コンサルティング・グループ株式会社代表取締役。
岐阜県出身。
2000年創業、2004年会社設立。
IT企業向け人材育成研修歴業界歴20年以上。
すべての無駄を省いた費用対効果の高い「筋肉質」な研修を提供します！
この記事に間違い等ありましたらぜひお知らせください。

学生時代は趣味と実益を兼ねてリゾートバイトにいそしむ。長野県白馬村に始まり、志賀高原でのスキーインストラクター、沖縄石垣島、北海道トマム。高じてオーストラリアのゴールドコーストでツアーガイドなど。現在は野菜作りにはまっている。