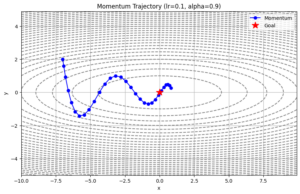
【講師向け】数式で挫折させない！「Adagrad」を直感的に教える『ぬかるみセンサー』の例え話

2026年1月26日 最終更新日時 : 2026年1月26日 山崎講師山崎講師

こんにちは。ゆうせいです。

ディープラーニングの研修をしていて、受講生の皆さんが一番苦戦する場所はどこでしょうか？

「誤差逆伝播法」もなかなかの強敵ですが、実は地味に厄介なのが「最適化アルゴリズム（Optimizer）」の種類ではないでしょうか。

SGD、Momentum、Adagrad、Adam……。

「先生、アルファベットばかりで何が違うのか分かりません！」

「数式の h って何ですか？ 高さですか？」

そんな悲鳴が聞こえてきそうです。

今日は、その中でも特に重要な転換点となる「Adagrad（アダグラッド）」について解説します。

これを理解すると、現代の最強アルゴリズムである「Adam」への理解もスムーズになります。

今回は、難解な数式を「賢いハイキングシューズ」に例えて、直感的に理解してもらう教え方をご紹介します。

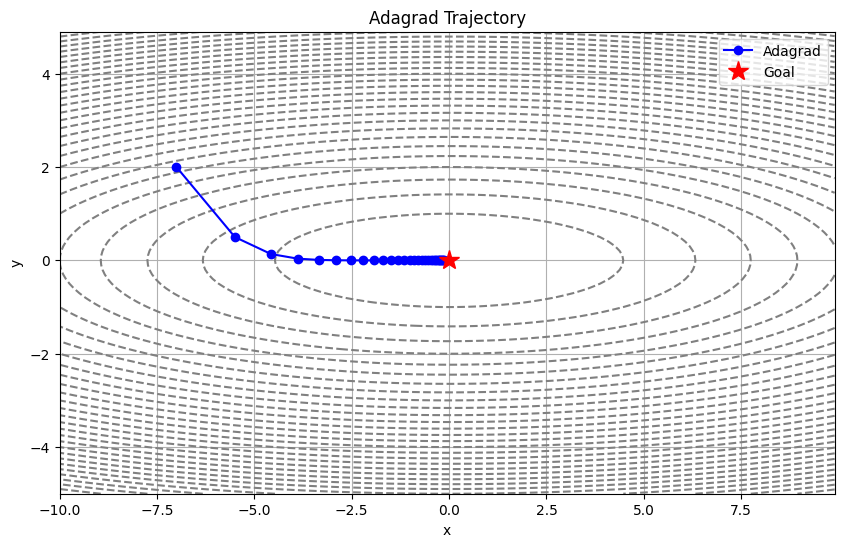
SGDの弱点とAdagradの画期的な点

まず、Adagradが登場する前の世界（SGD）を思い出してもらいましょう。

SGD（確率的勾配降下法）は、谷底を目指して山を降りるハイカーです。

しかし、彼は「常に歩幅が一定」という弱点を持っています。

  • 急な坂道でも、平坦な道でも、同じ歩幅で進む。
  • だから、急な坂では転げ落ちそうになり、平坦な道ではなかなか進まない。

そこで登場したのが Adagrad です。

正式名称は Adaptive Gradient Algorithm。「適応的勾配アルゴリズム」です。

生徒さんにはこう伝えてください。

「Adagrad は、足元を見て歩幅を自動調整してくれる、センサー付きの靴を履いたハイカーです」

重要な変数「 h 」は「足の疲れ」

Adagrad の数式には、必ず h という変数が登場します。

教科書的な説明では「勾配の二乗和」ですが、これでは誰もイメージできません。

ここは「足の疲れ（または、歩いた距離の記憶）」と説明しましょう。

このアルゴリズムは、以下のルールで動きます。

  1. よく動いたパラメータ（たくさん更新された道）は、 h （疲れ）が溜まる。
  2. h が溜まると、ブレーキがかかり、歩幅（学習率）が小さくなる。
  3. 逆に、今まであまり動いていないパラメータは、 h が小さいので、大きく踏み出す。

つまり、「今までたくさん勉強した部分は復習程度に、まだ勉強していない部分はガッツリやる」という、非常に効率的な学習スタイルなんです。

これを専門用語で「学習率減衰」と言いますが、「疲れに合わせてペース配分する」と言えば、高校生でも頷いてくれます。

数式の「ルート」と「割り算」の意味

では、先ほどの画像にあった数式（正解の選択肢）をもう一度見てみましょう。

$$W \leftarrow W - \eta \frac{1}{\sqrt{h}} \frac{\partial L}{\partial W}$$

この式を、日本語に翻訳します。

  • W ： 現在の場所
  • \eta （イータ）： 基本のやる気（学習率）
  • \frac{\partial L}{\partial W} ： 坂道の傾き（勾配）
  • \frac{1}{\sqrt{h}} ： ここが Adagrad の本体！

分母に h があることに注目させてください。

分母が大きくなる（疲れ h が溜まる）と、全体の値（更新量）は小さくなりますよね？

「たくさん動いて h が大きくなると、分母が大きくなって、ブレーキがかかる」

これが数式の意味です。

なぜ \sqrt{} （ルート）をつけるのか？ という鋭い質問が来たら、

「 h は二乗して足しているので、そのままだとブレーキが強すぎて止まってしまうからです。ルートをつけて次元（単位）を元に戻してあげるイメージですよ」

と答えてあげましょう。

Pythonコードで見る Adagrad の正体

それでは、実際のコードを見ながら解説します。

NumPyを使って実装すると、Adagrad の中身は驚くほどシンプルです。

以下は、研修でそのまま使えるサンプルコードです。

import numpy as np

class Adagrad:
    def __init__(self, lr=0.01):
        self.lr = lr        # 基本の学習率（eta）
        self.h = None       # 過去の勾配の記憶（初期値はNone）

    def update(self, params, grads):
        # 初回のみ h を初期化（0で埋め尽くされた辞書を作る）
        if self.h is None:
            self.h = {}
            for key, val in params.items():
                self.h[key] = np.zeros_like(val)

        for key in params.keys():
            # 【ここがポイント1】
            # 勾配を二乗して h に足し込む（過去の情報を蓄積）
            self.h[key] += grads[key] * grads[key]

            # 【ここがポイント2】
            # h のルートで割って、学習率を調整する
            # （1e-7 は 0 で割るのを防ぐための小さなお守り）
            params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7)

講師としての解説ポイント

コードを見せながら、以下の2点を強調してください。

  1. self.h[key] += grads[key] * grads[key]ここが「記憶」を作っている部分です。今の坂道の急さ（grads）を二乗して、これまでの合計（h）に足しています。ずっと足し算をしているので、 h の値は学習が進むにつれてどんどん大きくなります。
  2. params[key] -= ... / (np.sqrt(self.h[key]) + 1e-7)ここが「ブレーキ」の部分です。大きくなった h で割り算をしていますね。ちなみに 1e-7 （0.0000001）を足しているのは、もし h が 0 だった場合、割り算ができずにプログラムがエラー（ZeroDivisionError）で止まってしまうのを防ぐためです。「エアバッグ」みたいなものですね。

Adagrad のメリットと致命的な弱点

最後に、この手法の良い点と悪い点を伝えて、次の学習への意欲を掻き立てましょう。

メリット

パラメータ一つ一つに合わせて、個別に学習率を調整してくれるので、人間が細かく設定しなくても勝手にいい感じに学習が進みます。

デメリット

ここが重要です。

生徒さんに質問してみてください。

「 h は、ずっと足し算され続けます。学習をずーっと続けると、どうなると思いますか？」

答えは、「分母が巨大になりすぎて、更新量がゼロになる（学習が止まる）」です。

ブレーキがかかりすぎて、最終的に一歩も動けなくなってしまうのです。

この弱点を克服するために生まれたのが、過去の記憶を少しずつ忘れる機能を持った 「RMSProp」 や、さらに進化させた 「Adam」 なのです。

今日のまとめ

いかがでしたか？

  1. Adagrad は「足元を見て歩幅を変える賢い靴」
  2. 変数 h は「過去の勾配の二乗和（足の疲れ）」
  3. 疲れが溜まると、割り算でブレーキをかける
  4. でも、ブレーキがかかりすぎて止まってしまうのが玉に瑕

このように順を追って説明すれば、複雑な数式もコードも、意味のあるストーリーとして受講生の記憶に残ります。

次は、この Adagrad の弱点を克服した、現代AIのスタンダード「Adam」について解説する準備をしておきましょう！

それでは、また次の記事でお会いしましょう。

セイ・コンサルティング・グループでは新人エンジニア研修のアシスタント講師を募集しています。

投稿者プロフィール

山崎講師
山崎講師代表取締役
セイ・コンサルティング・グループ株式会社代表取締役。
岐阜県出身。
2000年創業、2004年会社設立。
IT企業向け人材育成研修歴業界歴20年以上。
すべての無駄を省いた費用対効果の高い「筋肉質」な研修を提供します！
この記事に間違い等ありましたらぜひお知らせください。

学生時代は趣味と実益を兼ねてリゾートバイトにいそしむ。長野県白馬村に始まり、志賀高原でのスキーインストラクター、沖縄石垣島、北海道トマム。高じてオーストラリアのゴールドコーストでツアーガイドなど。現在は野菜作りにはまっている。
対象読者
新人エンジニア研修講師
前の記事
【講師向け】SSD・YOLO・Faster R-CNNはどう違う？物体検出の「御三家」を初心者に直感的に解説する方法New!!
2026年1月26日
次の記事
【研修講師向け】「慣性」を味方につける！Momentumを物理の実験のように教えるテクニックNew!!
2026年1月26日