二項分布限定、期待値や分散の簡単な求め方

こんにちは。ゆうせいです。

これまでに「期待値」や「分散」のイメージを掴んでいただきましたね。

でも、もし「コインを100回投げたときは？」と聞かれたら、ひとつずつ計算するのは気が遠くなってしまいます。

そこで登場するのが、二項分布の公式です！

これを使えば、どれほど回数が増えても、まるで魔法のように一瞬で答えが導き出せます。

それでは、一緒にその公式の正体を見ていきましょう。

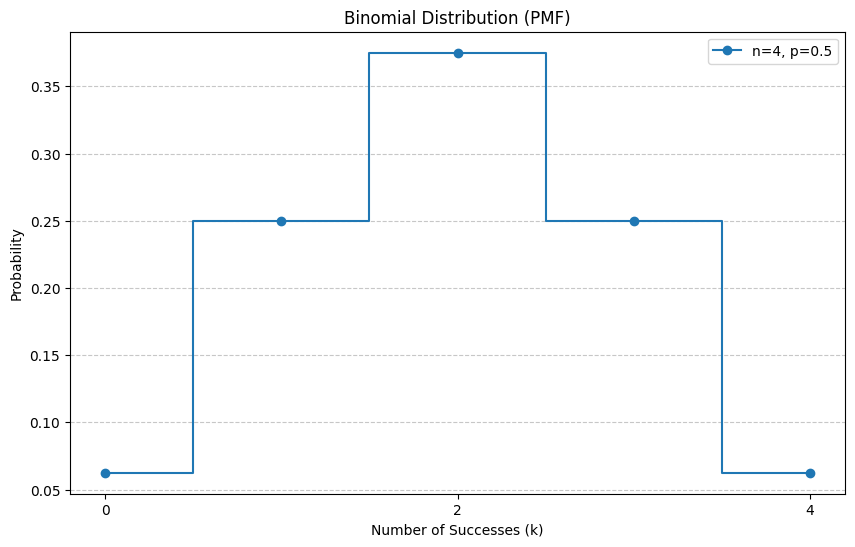
準備：3つの変数を設定しよう

公式を使う前に、まずは必要な情報を整理しましょう。

専門用語が出てきますが、中身はとてもシンプルです！

1. 試行回数 ：全部で何回チャレンジするか。今回は 4 です。
2. 成功確率 ：1回で表が出る確率。コインなので 0.5 です。
3. 失敗確率 ：1回で裏が出る確率。 で計算でき、今回は 0.5 です。

この 、 、 という3つの文字をパズルのように組み合わせるだけで、すべての答えが出てきます！

期待値は で求められる

期待値は、回数と確率を掛け合わせるだけでOKです。

「1回あたり の確率で表が出るなら、 回やれば くらいになるよね」という、とても直感的な式ですね。

期待値

今回の数字を当てはめてみましょう。

いかがですか？あっという間に期待値の 2 が導き出せました。

もし100回投げたなら、 と、一瞬で計算できますね！

分散は という絶妙なバランス

次に、データのバラつきを示す分散です。

分散の公式は、期待値にさらに「失敗する確率」を掛け合わせます。

分散

なぜ を掛けるのでしょうか。

それは、もし成功確率 が1（100パーセント成功）なら、バラつきは 0 になるはずだからです。

成功と失敗、両方の要素が混ざることで「ズレ」が生じる。そのバランスを表現しているのがこの式なのです。

計算してみると……

見事に分散の 1 が出てきました！

標準偏差は で単位を戻す

最後に、現実的なズレの目安である標準偏差です。

これは分散にルートを被せるだけ。

標準偏差

計算は以下の通りです。

これで、すべての主要な指標が公式だけで揃いました。

難しい合計計算をしなくても、 と さえ分かれば、その現象の正体が丸裸になってしまう。これが数学の持つパワーです！

メリットとデメリット

公式を使う際のポイントを整理しておきましょう。

メリット

• 計算ミスが劇的に減る。
• 回数がどれだけ増えても、同じ手間で答えが出せる。
• 複雑な現象を と という2つの要素だけで説明できる。

デメリット

• 公式を暗記しているだけでは、なぜそうなるかの理屈を忘れがちになる。
• 「表か裏か」のように、結果が2つに1つの現象（二項分布）にしか使えない。

ステップアップへの道標

公式を使いこなせるようになったあなたは、もうデータサイエンスの入り口に立っています！

この知識をさらに活かすために、次のステップへ進んでみましょう。

1. を0.5以外（例えば、当たりが10パーセントのくじ引きなど）に変えて計算してみる。
2. 回数 を極端に大きくして、グラフの形がどう変わるか想像してみる。
3. 「正規分布」という言葉を調べ、今回の二項分布とのつながりを探してみる。

公式は暗記するものではなく、道具として使い倒すものです。

皆さんの身の回りにある「確率」を、ぜひこの公式で分析してみてくださいね！

セイ・コンサルティング・グループでは新人エンジニア研修のアシスタント講師を募集しています。

投稿者プロフィール

山崎講師代表取締役

セイ・コンサルティング・グループ株式会社代表取締役。
岐阜県出身。
2000年創業、2004年会社設立。
IT企業向け人材育成研修歴業界歴20年以上。
すべての無駄を省いた費用対効果の高い「筋肉質」な研修を提供します！
この記事に間違い等ありましたらぜひお知らせください。

学生時代は趣味と実益を兼ねてリゾートバイトにいそしむ。長野県白馬村に始まり、志賀高原でのスキーインストラクター、沖縄石垣島、北海道トマム。高じてオーストラリアのゴールドコーストでツアーガイドなど。現在は野菜作りにはまっている。

最新の投稿

• 新人エンジニア研修講師2026年2月7日なぜ統計学に「円周率」が出てくるの？正規分布に隠された真ん丸な秘密
• 新人エンジニア研修講師2026年2月7日もう怖くない！統計学の不思議な文字「ガンマ」をマスターしよう
• 新人エンジニア研修講師2026年2月7日データが語る真実の見つけ方！パラメトリック統計学で推測の達人になろう
• 新人エンジニア研修講師2026年2月7日脳が仕掛ける錯覚の罠？アポフェニアとパレイドリアで「思い込み」を解き放とう