AIが賢くなる秘密の数式?ベイズの定理で「データから正解」を導き出す方法
こんにちは。ゆうせいです。
新人エンジニアのみなさん、AIが「この画像は 80% の確率で猫だ!」と判断するとき、裏側でどんな計算が行われているか知っていますか。
その核心にあるのが、統計学の超重要ルールであるベイズの定理です。
E資格でも頻出のこのテーマについて、今日はパズルを解くような感覚で学んでいきましょう。
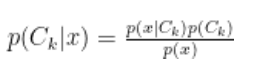
ベイズの定理とは「情報の更新」
ベイズの定理を一言でいうと、「新しいデータを得たときに、元々の予想をどれくらい修正すべきか」を計算する数式です。
高校数学の確率でつまずいた人も大丈夫。
要は、可能性のあるすべてのケースの中で、今起きていることが占める割合を計算しているだけなんです。
数式で書くと、こうなります。
ここで、 はすべてのクラスにおいてそのデータ
が発生する確率の合計です。
言葉で説明すると、「あるクラス に属する確率」を求めるには、そのクラスでの発生確率と、もともとそのクラスが出現する確率を掛け合わせ、それを全体で割ればいい、ということですね。
生成モデルの考え方
問題にもあった生成モデルでは、データ が各クラス
からどのように生成されるかを考えます。
- 事前確率
: データを手に入れる前に、そのクラスがそもそもどれくらい出現しやすいかという確率。
- 尤度(ゆうど)
: そのクラスだと仮定したときに、今回のデータ
が出現するもっともらしさ。
この 2 つを掛け合わせたものが、そのクラスである「勢力」になります。
すべてのクラスの勢力を足し合わせて、知りたいクラスの勢力がどれくらいのシェアを占めているかを計算すれば、それが答えになります!
練習問題:3つのメールフォルダの分類
それでは、ベイズの定理を使って、届いたメールが「仕事」「プライベート」「迷惑メール」のどれに属するかを判定してみましょう。
問題
あるメールに「お疲れ様です」という単語 が含まれていました。
それぞれのフォルダ における出現確率と、フォルダ自体の出現確率が以下のとき、このメールが「仕事」フォルダ
に属する確率を求めてください。
- 事前確率(フォルダの割合)
- 仕事
- プライベート
- 迷惑メール
- 仕事
- 尤度(「お疲れ様です」が含まれる確率)
- 仕事
- プライベート
- 迷惑メール
- 仕事
選択肢
- 0.4
- 0.5
- 0.8
- 0.87
解説と解答
ステップ1:各クラスの「勢力」を計算する
まずは、事前確率と尤度を掛け算します。
- 仕事の勢力:
- プライベートの勢力:
- 迷惑メールの勢力:
ステップ2:全体の合計  を出す
を出す
すべての勢力を足します。
ステップ3:仕事フォルダのシェアを計算する
全体の 0.46 のうち、仕事の 0.40 が占める割合を計算します。
四捨五入すると 0.87 になりますね。
正解は 4 番です!
メリットとデメリット
メリット
- 少ないデータでも推論できる: まったく未知の事態でも、事前の予想(事前確率)を置くことで計算が始められます。
- 根拠が明確: なぜその確率になったのか、計算過程が論理的なので人間に説明しやすいです。
デメリット
- 事前確率に左右される: 最初の予想(事前確率)が的外れだと、結果も大きくズレてしまいます。
- 計算量: 扱うクラスやデータの種類が膨大になると、分母の計算が非常に大変になります。
今後の学習の指針
ベイズの定理の感覚が掴めたら、次は以下のステップに進みましょう。
- ナイーブベイズ分類器: 複数の単語からメールを分類するアルゴリズムを学んでみてください。
- 共役事前分布: 計算を楽にするための数学的なテクニックを覗いてみましょう。
- MCMC法: 複雑すぎて計算できない分母を、シミュレーションで近似する方法を調べてみてください。
確率は「絶対」を扱わないからこそ、現実世界の曖昧な問題を解く強力な武器になります。
セイ・コンサルティング・グループの新人エンジニア研修のメニューへのリンク
投稿者プロフィール

- 代表取締役
-
セイ・コンサルティング・グループ株式会社代表取締役。
岐阜県出身。
2000年創業、2004年会社設立。
IT企業向け人材育成研修歴業界歴20年以上。
すべての無駄を省いた費用対効果の高い「筋肉質」な研修を提供します!
この記事に間違い等ありましたらぜひお知らせください。
学生時代は趣味と実益を兼ねてリゾートバイトにいそしむ。長野県白馬村に始まり、志賀高原でのスキーインストラクター、沖縄石垣島、北海道トマム。高じてオーストラリアのゴールドコーストでツアーガイドなど。現在は野菜作りにはまっている。
最新の投稿
 新人エンジニア研修講師2026年2月28日f(x, y) とf(x; y) って何が違うの? コピー
新人エンジニア研修講師2026年2月28日f(x, y) とf(x; y) って何が違うの? コピー 新人エンジニア研修講師2026年2月28日f(x, y) とf(x; y) って何が違うの?
新人エンジニア研修講師2026年2月28日f(x, y) とf(x; y) って何が違うの? 新人エンジニア研修講師2026年2月28日AIの深層へようこそ!逆伝播バックプロパゲーションの仕組みを完全マスター
新人エンジニア研修講師2026年2月28日AIの深層へようこそ!逆伝播バックプロパゲーションの仕組みを完全マスター 新人エンジニア研修講師2026年2月28日機械学習で必須のscikit-learn関数ベスト10
新人エンジニア研修講師2026年2月28日機械学習で必須のscikit-learn関数ベスト10
