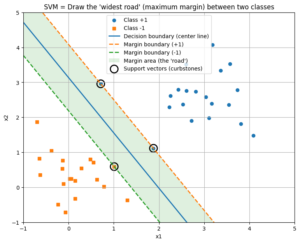
【数学の記号】その2本の棒は「ノルム」！ベクトルの「長さ」を測るメジャー

こんにちは。ゆうせいです。

このような質問をいただきました。

「絶対値記号のような2本の縦棒 は何ですか？」

鋭い質問ですね！

「絶対値の記号（ ）に似ているな」と思ったその感覚、大正解です。

あの2本の縦棒 の正体は、「ノルム（Norm）」と呼ばれるものです。

一言で言うと、「ベクトルの『長さ』や『距離』を表す記号」です。

エンジニアとして数式を読むときに絶対に避けて通れないこの記号について、絶対値との違いを交えてサクッと解説しますね。

1. 絶対値の「兄貴分」だと思えばOK

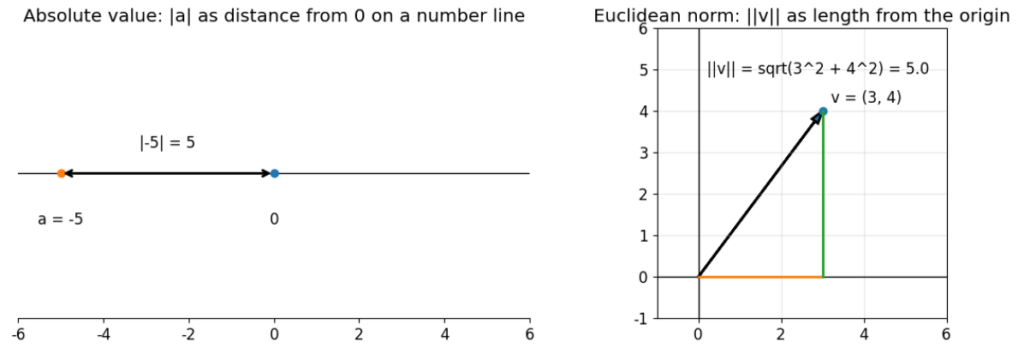
まず、私たちがよく知っている「絶対値」を思い出してください。

• 絶対値 ：数直線上で、「0」からどれくらい離れているか（距離）を表します。例： （マイナス5は、0から5歩離れている）

これに対して、「ノルム」はこうです。

• ノルム ：広い空間（2次元や3次元以上）で、「原点」からどれくらい離れているか（距離・長さ）を表します。

つまり、「数字が1個なら絶対値（棒1本）、数字がセット（ベクトル）になったらノルム（棒2本）」と使い分けているだけなんです。

※教科書によっては、ベクトルでも棒1本 で書くこともありますが、意味は同じです。棒2本の方が「これはベクトルだよ！」と強調されるので、誤解がなくて親切な書き方です。

2. 具体的には「三平方の定理」

では、具体的にどう計算するのでしょうか？

これは中学校で習った「三平方の定理（ピタゴラスの定理）」そのものです。

たとえば、 というベクトル（座標）があったとします。

原点 からこの点までの「直線の長さ」はいくつでしょう？

答えは5です。この「5」という長さのことを、数学語で と書くのです。

3. 今回の式での意味

質問していただいたRBFカーネルの式に出てくるのは、引き算が入ったこの形でしたね。

これは、「データ と、データ の間の直線距離」を表しています。

• ：2つの地点の「ズレ（差のベクトル）」を計算。
• ：そのズレの「長さ」を測る。

つまり、あの数式全体は、

「2つのデータ間の距離（ ）を計算して、それを2乗しなさい」

という指示だったのです。

まとめ

• 棒1本 は、ただの数の大きさ（絶対値）。
• 棒2本 は、ベクトルの長さ（ ノルム ）。
• 正体は、おなじみの 「三平方の定理」 。

これからこの2本線を見たら、

「おっ、ここからここまでのメジャーで測った距離のことだな」

と脳内で翻訳してあげてください。それだけで、数式の景色がガラッと変わって見えますよ！

セイ・コンサルティング・グループの新人エンジニア研修のメニューへのリンク

投稿者プロフィール

山崎講師代表取締役

セイ・コンサルティング・グループ株式会社代表取締役。
岐阜県出身。
2000年創業、2004年会社設立。
IT企業向け人材育成研修歴業界歴20年以上。
すべての無駄を省いた費用対効果の高い「筋肉質」な研修を提供します！
この記事に間違い等ありましたらぜひお知らせください。

学生時代は趣味と実益を兼ねてリゾートバイトにいそしむ。長野県白馬村に始まり、志賀高原でのスキーインストラクター、沖縄石垣島、北海道トマム。高じてオーストラリアのゴールドコーストでツアーガイドなど。現在は野菜作りにはまっている。

最新の投稿

• 山崎講師2026年1月9日【数学の罠】「log」の底は10かeか2か？文脈で見分けるエンジニアのための生存戦略
• 山崎講師2026年1月9日【線形代数】あの「串刺し団子」みたいな記号は何？「Φ（ファイ）」の使い方を徹底解説
• 山崎講師2026年1月9日【数学の記号】その2本の棒は「ノルム」！ベクトルの「長さ」を測るメジャー
• 山崎講師2026年1月9日【カーネル法】無限の空間へワープ！「動径基底関数（RBF）カーネル」の正体を数式で暴く