【機械学習】「SVM」はなぜ最強だったのか？データを分ける「一番太い道路」の引き方
山崎講師こんにちは。ゆうせいです。
前回は、データを赤チームと青チームに分ける境界線、決定境界についてお話ししました。「確率0.5の場所に線を引く」というロジスティック回帰のアプローチでしたね。
しかし、ここで一つ問題があります。
「データを分ける線」というのは、実は無数に引けてしまうのです。
ギリギリ赤チームの近くを通る線でもいいし、青チームすれすれの線でも、一応分類はできます。
では、その無数の線の中で、「もっとも良い線」とはどれなのでしょうか？
この問いに、数学的に美しく、そして最強の答えを出したのが「サポートベクターマシン（SVM）」です。
ディープラーニングが流行する前、機械学習の世界で「王様」と呼ばれていたこのアルゴリズム。今日はその強さの秘密である「マージン最大化」という考え方を、新人エンジニアのみなさんに解説します。
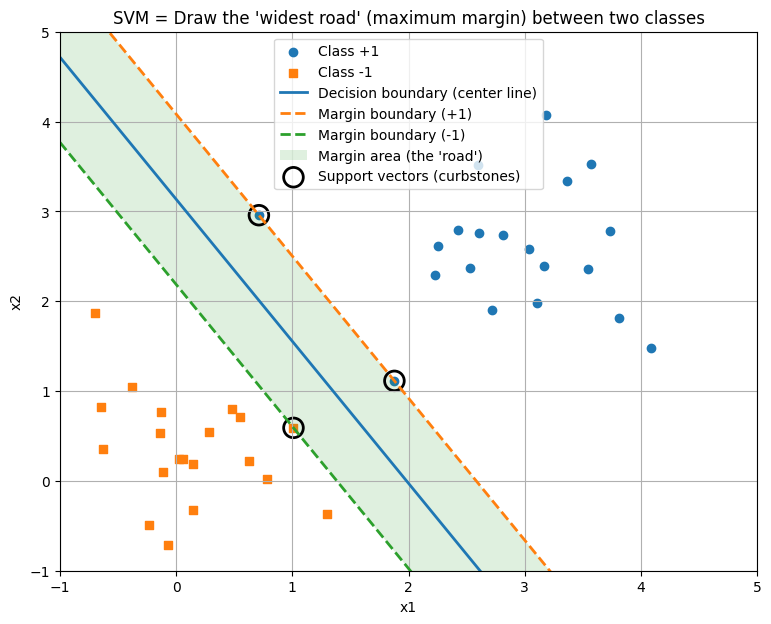
ギリギリを攻めるな！「余裕」を持て
SVMの考え方はとてもシンプルです。
「境界線は、データからできるだけ離れた真ん中に引くべきだ」
というものです。
想像してください。
あなたは赤と青のボールが散らばっている広場に、チームを分けるための「道路」を作ろうとしています。
細いロープを一本置くだけでは不安ですよね？ 風で飛んでしまうかもしれませんし、新しいボールが転がってきたときに、どっちのチームか判定しづらくなります。
そこでSVMはこう考えます。
「赤チームの最前列」と「青チームの最前列」。この両者の間隔を限界まで広げて、「一番太い道路」を通そう！
この「道路の幅」のことを、専門用語で「マージン（Margin）」と呼びます。
- 道路の中心線
決定境界
- 道路の幅
このマージンを最大にするように線を引けば、未知のデータが来たときも、余裕を持って正しく分類できるはずです。これを「マージン最大化」と呼びます。
崖っぷちを歩くより、広い道の真ん中を歩くほうが安全ですよね。SVMは、この「安全性（汎化性能）」を数学的に保証してくれるのです。
名前の由来「サポートベクター」とは？
さて、この手法の名前になっている「サポートベクター（Support Vector）」とは何でしょうか？
直訳すると「支えるベクトル」です。
先ほどの道路の話に戻りましょう。
道路の幅を決めるとき、重要なのはどのボールでしょうか？
チームの後ろの方にいるボールなんて、道路から遠いので関係ありませんよね。
重要なのは、「道路のギリギリ一番近くにいるボールたち」だけです。
この、最前線にいて道路の幅（マージン）を決定づけている重要なデータのことを、「サポートベクター」と呼びます。
これにはすごいメリットがあります。
SVMは、線を引くために「すべてのデータ」を見る必要がないのです。最前列の数個のデータ（サポートベクター）さえ見ていれば、計算ができてしまいます。
だから、データが大量にあっても、計算が効率的で無駄がないのです。
直線で分けられないなら「次元」を変えろ！
SVMにはもう一つ、必殺技があります。それが「カーネル法（Kernel Trick）」です。
世の中には、直線一本ではどうしても分けられないデータがあります。
例えば、紙の上に「赤チームが中心に集まっていて、その周りを青チームがドーナツ状に囲んでいる」状態を想像してください。
どう直線を引いても、きれいに分けることはできませんよね。
そこでSVMは、魔法を使います。
「この紙（2次元）を、空間（3次元）に浮かび上がらせよう！」
机の上にあるデータを、3次元空間にマッピングし直します。
たとえば、中心に近い赤チームだけを「空中に持ち上げる」ような変換をするのです。
するとどうでしょう。
「空中の赤チーム」と「机の上の青チーム」の間に、下敷き（平面）を一枚、スッと差し込むことができますよね？
3次元空間で平面を使って分けたあと、それを元の2次元に戻して見ると、境界線はドーナツ型のきれいな「曲線」になっています。
このように、低次元では分けられないものを、高次元に移動させてスパッと分けるテクニック。これがカーネル法の正体です。
メリットとデメリット
かつて最強と言われたSVMにも、得意不得意があります。
メリット
- 精度が高い：マージンを最大化するため、未知のデータに対する予測精度（汎化性能）が非常に高いです。
- 外れ値に強い：マージンという「遊び」があるおかげで、少しくらい変なデータがあっても境界線が大きくズレません。
- 非線形もいける：カーネル法を使えば、複雑な形の境界線も引けます。
デメリット
- データが巨大すぎると遅い：数万件くらいまでは最強ですが、数百万、数億件のビッグデータになると計算に時間がかかりすぎます（これがディープラーニングに主役を譲った理由の一つです）。
- 確率が出ない：ロジスティック回帰のように「確率は70%です」といった数値は出せません。「白か黒か」の判定結果だけが返ってきます。
まとめ：一番安全な道を選べ
ここまで読んでいただき、ありがとうございます。
SVMがなぜ愛されてきたのか、その理由がわかりましたか？
- ただ線を引くのではなく、「一番太い道路（マージン）」を引く。
- 最前列のデータ「サポートベクター」だけが重要。
- 「カーネル法」で次元を超えてデータを分ける。
新人エンジニアのみなさんが、「データ数はそこまで多くないけど、とにかく高精度に分類したい！」という場面に出くわしたら、迷わずこのSVMを使ってみてください。きっと期待に応えてくれるはずです。
今後の学習の指針
SVMの次は、いよいよ現在のAIの主流である「ニューラルネットワーク（ディープラーニング）」の世界へ足を踏み入れてみましょう。
SVMが「少数の精鋭（サポートベクター）」で戦う手法だとすれば、ニューラルネットワークは「圧倒的な数の力」で戦う手法です。
まずは、その最小単位である「パーセプトロン」について調べてみてください。
それでは、また次回の記事でお会いしましょう！
セイ・コンサルティング・グループの新人エンジニア研修のメニューへのリンク
投稿者プロフィール
