【新人エンジニア研修】対数の微分がなぜ分数になるのか？直感と論理で教える技術

2026年1月13日 2026年1月13日山崎講師

山崎講師

こんにちは。ゆうせいです。

新人エンジニアの研修を担当されているみなさん、毎日の講義お疲れ様です。講義の中で、数学的な概念を説明しなければならない場面に出くわすことはありませんか。

たとえば、アルゴリズムの計算量やデータ分析の基礎を教える際、対数（ログ）が登場します。そこで鋭い新人からこんな質問が飛んでくるかもしれません。

「先生、どうして対数 $\log x$ を微分すると、あんなに形が違う $\frac{1}{x}$ という分数になってしまうんですか？」

この問いに、あなたは一瞬で、そして誰もが納得できるように答えられますか。

公式だから覚えなさい、と片付けるのは簡単です。しかし、それではエンジニアとしての「なぜ？」を掘り下げる力が育ちません。

今日は、この不思議な数式の成り立ちを、数式が苦手な方でも人に教えられるレベルまで噛み砕いて解説します。直感的なイメージと、少しの厳密さを行き来しながら、一緒に正解への道筋を探っていきましょう。

なぜ「カーブ」が「分数」になるのか

まず、この数式の違和感の正体を探ります。

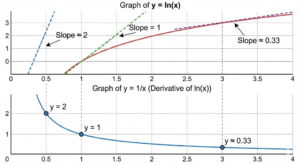
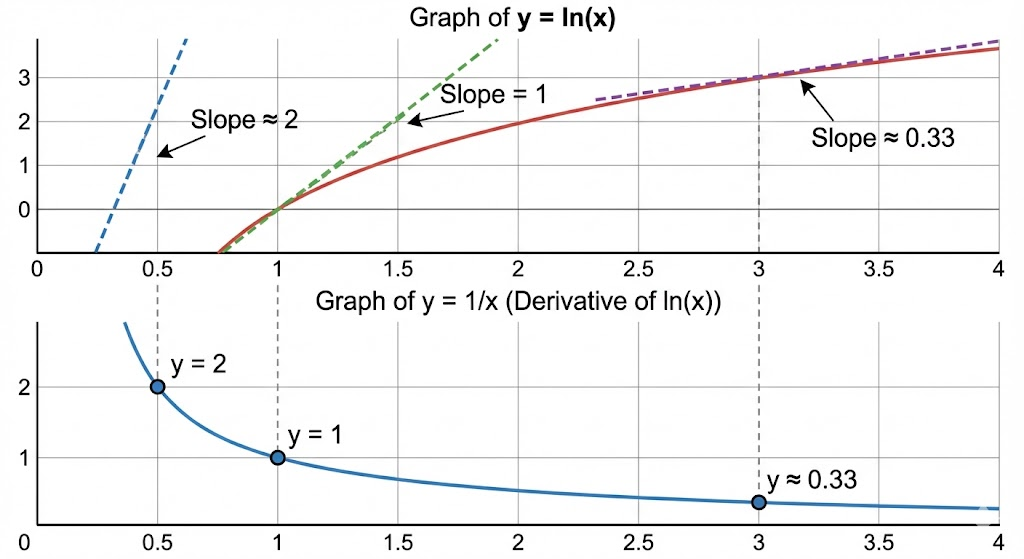
対数のグラフを思い浮かべてみてください。ゆっくりと右上がりに伸びていく、あのなだらかな曲線です。一方で、 $\frac{1}{x}$ という分数のグラフは、反比例の形をしていますね。

形がまったく違うのに、なぜ微分という操作でつながるのでしょうか。

ここで重要なキーワードが「接線の傾き」です。

微分とは、ある一点における変化の割合、つまりグラフの傾きを求めることです。対数グラフの右側、つまり $x$ が大きいところを見てください。グラフはどんどん平坦になっていますよね。

平坦ということは、傾きが小さいということです。

逆に、左側の $x$ が小さいところはどうでしょう。グラフは急激に立ち上がっています。つまり、傾きが大きいのです。

$x$ が大きいとき、傾き（微分結果）は小さい。
$x$ が小さいとき、傾き（微分結果）は大きい。

この関係を見事に表しているのが、分数の $\frac{1}{x}$ なのです。分母が大きくなれば全体は小さくなり、分母が小さくなれば全体は大きくなりますからね。直感的には、このように「勢いが逆転する関係」と捉えると説明しやすくなります。

ネイピア数がつなぐ論理の架け橋

直感的な理解ができたら、次は少しだけ数式の森へ足を踏み入れましょう。ここで登場する主役が「ネイピア数 $e$ 」です。

高校数学で習った微分の定義式を思い出してください。変化の割合の極限をとる、あのアプローチです。

まず、関数 $f(x)$ を $\log x$ と置きます。ここでの対数は、特に断りがない限り自然対数（底が $e$ ）とします。

微分の定義に従って式を作ると、次のようになります。

$f'(x) = \lim_{h \to 0} \frac{\log(x + h) - \log x}{h}$

ここで対数の性質を使います。引き算は真数（ログの中身）の割り算に変形できましたね。

$= \lim_{h \to 0} \frac{1}{h} \log \left( \frac{x + h}{x} \right)$

括弧の中身を少し整理してみましょう。

$= \lim_{h \to 0} \frac{1}{h} \log \left( 1 + \frac{h}{x} \right)$

ここからが魔法のような展開です。少しテクニカルですが、ついてきてくださいね。式を見やすくするために、 $\frac{h}{x}$ を $t$ という別の文字に置き換えます。すると、 $h$ が $0$ に近づくとき、 $t$ も $0$ に近づきます。また、 $\frac{1}{h}$ は $\frac{1}{xt}$ と書き換えられます。

式を書き換えてみましょう。

$= \lim_{t \to 0} \frac{1}{xt} \log(1 + t)$

ここで、対数の前に付いている係数を、対数の中身の指数（右上の乗数）に持ってきます。

$= \lim_{t \to 0} \frac{1}{x} \log(1 + t)^{\frac{1}{t}}$

さあ、注目してください。ログの中にある $(1 + t)^{\frac{1}{t}}$ という部分。これこそが、ネイピア数 $e$ の定義そのものなのです。 $t$ を限りなく $0$ に近づけると、この部分は $e$ になります。

つまり、極限をとるとこうなります。

$= \frac{1}{x} \log e$

自然対数の底は $e$ ですから、 $\log e$ は $1$ です。結果として、きれいな分数だけが残ります。

$= \frac{1}{x}$

いかがでしょうか。単なる記号操作のように見えますが、この変形の裏には「自然な成長の速度」を表すネイピア数の性質が隠れていたのです。

深く理解することのメリットとデメリット

さて、ここまで詳しく解説してきましたが、研修生の全員にこの証明を教えるべきでしょうか。ここで、指導者として知っておくべきメリットとデメリットを整理します。

メリット

一つ目のメリットは、応用力がつくことです。

ただ公式を暗記しているだけでは、底が $e$ 以外の対数（常用対数や二進対数）が出てきたときに手が止まってしまいます。導出過程を知っていれば、係数がどう変化するかを自分で導き出せます。

二つ目のメリットは、数学へのアレルギーを減らせることです。

「なぜ？」が解決したときのスッキリ感は、学習意欲を大きく高めます。特にエンジニアは理屈で納得したい生き物ですから、論理的な背景を知ることで安心感を得られるでしょう。

デメリット

一方で、デメリットもあります。それは、時間がかかることです。

限られた研修期間の中で、微分の定義から解説するのはタイムロスになる可能性があります。

また、数学が極端に苦手な初学者にとっては、 $\lim$ や $e$ の定義が出てきた時点で思考停止してしまうリスクがあります。難しすぎて自信を喪失させてしまっては本末転倒です。

指導の現場でどう活かすか

では、どうすればよいのでしょうか。

おすすめなのは、相手のレベルに合わせて説明の深さを調整することです。

まずは、最初に紹介した「グラフの傾き」の話をしてみてください。「右に行くほど坂が緩やかになるから、値は小さくなるんだよ」という直感的な説明は、誰にでも響きます。

その上で、数学が得意な研修生や、もっと詳しく知りたいという質問が出たときに初めて、ネイピア数を使った証明を披露するのです。

「実はね、ここには自然界の成長法則が隠されているんだよ」

そう前置きをして、ホワイトボードにさらさらと数式を書くことができれば、あなたの講師としての信頼度は間違いなくアップするでしょう。

今後の学習の指針

最後に、この知識を足がかりにして、新人のみなさんにどのような学習を促すべきかをお話しして締めくくります。

対数の微分を理解したら、次は「積分」へと視点を広げてみてください。 $\frac{1}{x}$ を積分すると $\log x$ に戻るという事実は、物理現象や経済の動きを理解する上で非常に強力なツールになります。

また、アルゴリズムの分野では「計算量」の理解に直結します。なぜ二分探索が速いのか、なぜクイックソートが効率的なのか。その背景にある対数の感覚を、数式を通じて養っていってください。

学ぶことは山のようにありますが、一つひとつの「なぜ？」を大切にすることで、必ず力強いエンジニアへと成長できるはずです。

みなさんの講義が、新人エンジニアたちの未来を明るく照らすことを願っています。

それでは、またお会いしましょう。

セイ・コンサルティング・グループでは新人エンジニア研修のアシスタント講師を募集しています。

投稿者プロフィール

山崎講師代表取締役

セイ・コンサルティング・グループ株式会社代表取締役。
岐阜県出身。
2000年創業、2004年会社設立。
IT企業向け人材育成研修歴業界歴20年以上。
すべての無駄を省いた費用対効果の高い「筋肉質」な研修を提供します！
この記事に間違い等ありましたらぜひお知らせください。

学生時代は趣味と実益を兼ねてリゾートバイトにいそしむ。長野県白馬村に始まり、志賀高原でのスキーインストラクター、沖縄石垣島、北海道トマム。高じてオーストラリアのゴールドコーストでツアーガイドなど。現在は野菜作りにはまっている。