線形代数と機械学習の関係を新人エンジニアに解説
山崎講師こんにちは。ゆうせいです。
今日は「線形代数と機械学習の関係」についてお話しします。線形代数と聞くと、行列やベクトルの計算が延々と続く難しい数学というイメージを持つ人が多いですが、実は機械学習を支える大黒柱なんです。
なぜ線形代数が必要なのか？
機械学習では「データを数値として扱う」ことが基本になります。文章や画像、音声のような複雑なものも、最終的には数の集まりとして計算可能な形に変換します。
その「数の集まり」を効率よく扱うのに使われるのがベクトルや行列、つまり線形代数の道具なんです。
例えるなら、線形代数は「データを整理して計算するための箱とルール」。データサイエンスという工場を動かすための基盤部分、と考えてください。
機械学習で出てくる具体例
- データの表現
- 画像はピクセル値を並べた行列
- テキストは単語ごとの数値ベクトル
- ユーザーと商品の関係は行列
- モデルの学習
ニューラルネットワークでは入力に「行列の掛け算」が大量に登場します。
例えば、中間層を通す処理は次のような形です。
y = Wx + b
ここでW は重み行列x は入力ベクトルb はバイアスベクトルy は出力ベクトルこれは線形代数そのものです。 - 次元削減（特徴抽出）
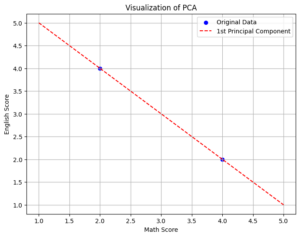
PCA（主成分分析）やSVD（特異値分解）といった手法は、データを小さい次元に圧縮するために線形代数の分解法を使います。
たとえば「100次元のデータを2次元に落とす」といった処理は、線形代数の計算によって可能になります。 - 類似度の計算
先ほど学んだ「コサイン類似度」も内積を使って計算します。これも線形代数の一部ですね。
メリットとデメリット
メリットは「抽象的なデータ処理をシンプルに表現できる」ことです。
逆にデメリットは「初学者には抽象的すぎる」こと。数式がデータ処理やモデルの学習の裏でどう動いているのかをイメージするのが難しいかもしれません。
例えで理解
線形代数を「交通インフラ」に例えてみましょう。
- ベクトル：車1台
- 行列：道路網（車をある場所から別の場所に移動させる仕組み）
- 行列演算：多くの車を効率よく移動させる信号や道路設計
機械学習という都市を動かすには、交通インフラ（線形代数）が不可欠なんです。
まとめ
- データはベクトルや行列で表現される
- 学習の計算はほぼすべて線形代数
- 特徴抽出や次元削減も線形代数
- 類似度計算も内積などの線形代数
つまり「線形代数なしで機械学習は動かない」と言っても過言ではありません。
次のステップとしては「行列の掛け算」と「固有値・固有ベクトル」から勉強を始めると、機械学習の数学的基盤がどんどん見えてきますよ！
さて、あなたが今扱っているデータを「ベクトルや行列」として表すと、どんな姿になりそうでしょうか？
セイ・コンサルティング・グループの新人エンジニア研修のメニューへのリンク
投稿者プロフィール
- 代表取締役
-
セイ・コンサルティング・グループ株式会社代表取締役。
岐阜県出身。
2000年創業、2004年会社設立。
IT企業向け人材育成研修歴業界歴20年以上。
すべての無駄を省いた費用対効果の高い「筋肉質」な研修を提供します！
この記事に間違い等ありましたらぜひお知らせください。
