2桁の平方数の覚え方
平方数、つまりある数を自分自身で掛け合わせた結果として得られる数について学ぶことは、数学の基礎を固める上で非常に重要です。特に、2桁の平方数を覚えることは、計算のスピードを上げたり、数学の問題を効率的に解くための役立つスキルです。でも、2桁の数は少し多くて覚えるのが難しいかもしれませんね。そこで、簡単に覚えるための方法をいくつか紹介します。
1. 数字の特徴を利用する
まず、2桁の平方数にはいくつかの特徴があります。これらの特徴を知ることで、数字をより覚えやすくすることができます。
1-1. 桁数に注目する
2桁の平方数は、100から最大で961まで存在します。これは10の2乗(100)から31の2乗(961)までの範囲に収まります。つまり、平方数の結果は100以上1,000未満の数になるということです。このことを頭に入れておくと、平方数を計算するときの結果の範囲を予測しやすくなります。
2. 数のパターンを活用する
平方数は計算結果に特定のパターンがあるため、これを利用して覚えましょう。
2-1. 終わりの数字に注目する
例えば、次のような規則があります:
- 数字が5で終わる数(15, 25など)の平方数は、常に25で終わります。
- 数字が0で終わる数(10, 20など)の平方数は、常に00で終わります。
これにより、例えば「25の平方数は625」というように、覚えやすくなります。
3. 具体的な覚え方
それでは、いくつかの2桁の平方数を覚えるためのコツを紹介します。
3-1. 語呂合わせを使う
語呂合わせは、数字を言葉に置き換えることで覚えやすくする方法です。例えば、
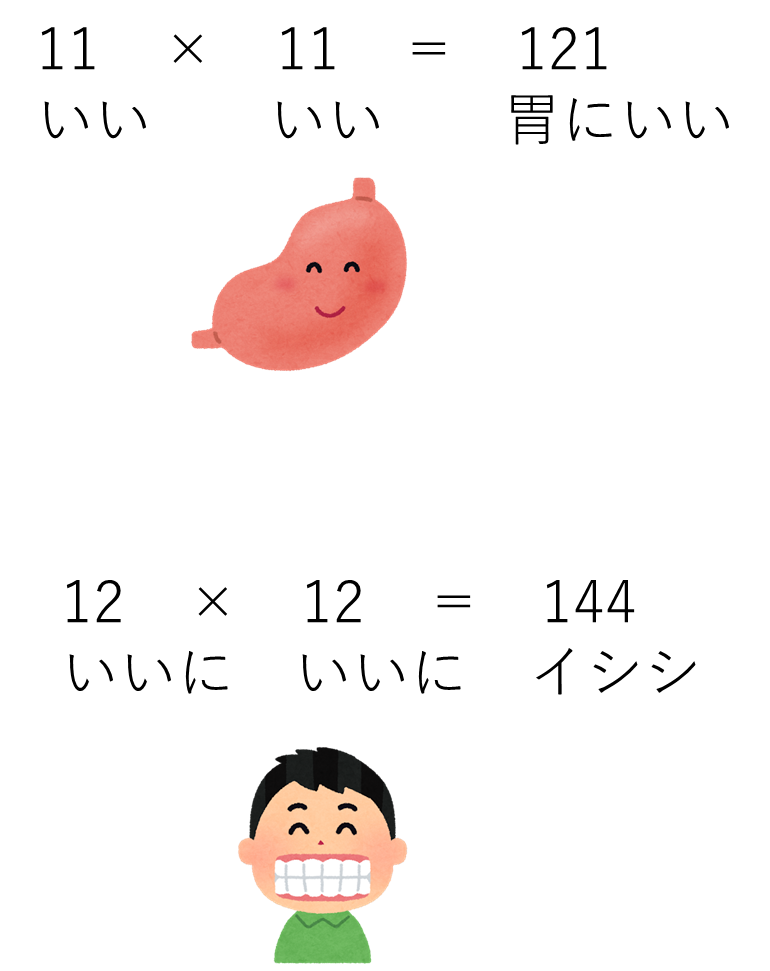




このように、数字をリズミカルな言葉に変えることで、記憶に残りやすくなります。
3-2. パターンを見つける
例えば、10の平方数 = 100、20の平方数 = 400、30の平方数 = 900 のように、10ごとの数の平方数は100の単位で増えていくことを覚えると、次の数も予測しやすくなります。
3-3. 繰り返し書く
最後に、繰り返し書くことも効果的です。10から31までの数を何度も書いて覚えることで、体が覚えていきます。書くことで、目で見て、手で書いて、頭で考えるという三重の刺激を受けるため、記憶に残りやすくなります。
今後の学習の指針
2桁の平方数を覚えることは、計算力を高めるための第一歩です。次に進むべき学習としては、平方数の性質をより深く理解したり、平方根の計算を学んだりすると良いでしょう。また、他の数の乗数や平方数の応用問題に取り組むことで、数学の力をさらに強化できます。繰り返し学習し、自分に合った覚え方を見つけることが大切です。これからも楽しみながら数学を学んでいきましょう!
投稿者プロフィール

- 代表取締役
-
セイ・コンサルティング・グループ株式会社代表取締役。
岐阜県出身。
2000年創業、2004年会社設立。
IT企業向け人材育成研修歴業界歴20年以上。
すべての無駄を省いた費用対効果の高い「筋肉質」な研修を提供します!
この記事に間違い等ありましたらぜひお知らせください。
学生時代は趣味と実益を兼ねてリゾートバイトにいそしむ。長野県白馬村に始まり、志賀高原でのスキーインストラクター、沖縄石垣島、北海道トマム。高じてオーストラリアのゴールドコーストでツアーガイドなど。現在は野菜作りにはまっている。

