信頼区間とは?
信頼区間(しんらいくかん)は、統計学における非常に重要な概念の一つです。簡単に言えば、「あるデータから推定された母集団の真の値が、ある範囲内にあるだろう」ということを示すものです。信頼区間は通常、データの平均や割合、相関係数などの推定値に対して用いられます。
例えば、あるクラスの生徒のテストの平均点を調査したとしましょう。その調査結果から、クラス全体の平均点が60点であると推定されたとします。しかし、これだけでは推定にどれくらいの不確かさがあるのかがわかりません。ここで信頼区間が役立ちます。
信頼区間は、「この範囲に真の平均点が存在する可能性が高い」と示してくれるわけです。例えば、「95%の信頼度で、真の平均点は55点から65点の間にある」といった形で表現されます。
信頼区間の構成要素
信頼区間には以下の3つの要素が含まれています:
- 点推定値(Point Estimate)
これは、データから計算された特定の値です。先ほどの例では、60点が点推定値にあたります。 - 信頼度(Confidence Level)
通常は百分率で表され、母集団の真の値が信頼区間内に含まれる確率を示します。95%や99%がよく使われる値です。95%の信頼度とは、「同じ調査を100回行ったとすると、そのうち95回は真の値がこの区間に入るだろう」という意味です。 - 誤差範囲(Margin of Error)
点推定値の周りにどれだけの誤差があるかを示します。誤差が大きいほど信頼区間も広くなります。
具体的な計算方法
信頼区間の計算にはいくつかの方法がありますが、ここでは代表的な例として「平均値の信頼区間」を考えます。
平均値の信頼区間の計算
- 点推定値の計算
まず、データの平均値を計算します。これが点推定値です。 - 標準誤差の計算
標準誤差(Standard Error)は、標準偏差(Standard Deviation)をサンプルサイズの平方根で割ったものです。これにより、平均値のばらつきの大きさを把握できます。

信頼区間の幅の計算
信頼区間の幅は、標準誤差に信頼度に対応する値(通常はz値やt値)を掛けたものです。95%の信頼度では、z値は約1.96です。
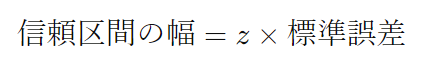
信頼区間の計算
最後に、点推定値から信頼区間の幅を引いたものが下限、加えたものが上限となります。

例
例えば、ある学校の10人の生徒のテストの点数が以下の通りだったとします:
55, 60, 65, 70, 75, 80, 85, 90, 95, 100
このデータの平均点は75点、標準偏差は14.87点とします。この場合の標準誤差は約4.70となります。95%の信頼度で信頼区間を計算すると、信頼区間の幅は約9.21点になります。したがって、信頼区間は以下のようになります。
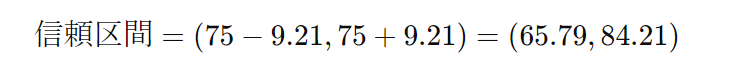
この結果は、「95%の信頼度で、この学校の全生徒の平均点は65.79点から84.21点の間にある」と解釈できます。
信頼区間の意味と注意点
信頼区間は非常に有用なツールですが、正しく理解して使うことが重要です。信頼区間が示すのは「確実な範囲」ではなく、「ある程度の確率で真の値が含まれる範囲」です。また、信頼区間が狭い方が良いとされがちですが、データのばらつきが大きい場合やサンプルサイズが小さい場合、信頼区間は広くなりがちです。
また、信頼区間は「母集団の真の値」が区間内に含まれるかどうかを示すものではありません。95%の信頼区間があるということは、5%の確率でその区間外に真の値が存在する可能性があることを意味します。
二項分布と正規分布の近似
100枚のコインを同時に投げるとき、表が出る枚数の予言を行うために、95%の信頼区間を計算します。この問題では二項分布を使用しますが、コインの枚数が多いので、正規分布に近似して計算する方法を採用します。
コインを投げたとき、表が出る確率を p=0.5とします。表が出る枚数 Xは、試行回数 n=100の二項分布に従います。二項分布は次のように表されます。
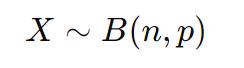
しかし、今回は nが大きいので、正規分布を用いて近似できます。正規分布では、平均 μ と標準偏差 σ が次のように計算されます。
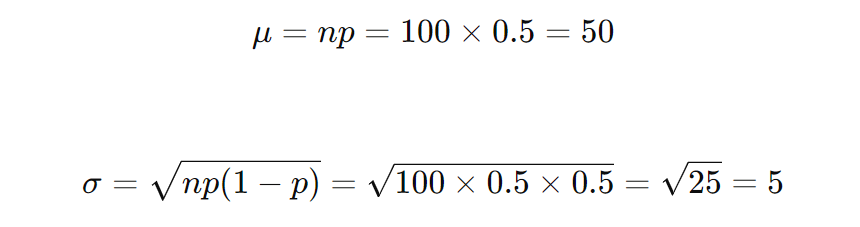
95%信頼区間の計算
95%の信頼区間は、標準正規分布 Zにおいて ±1.9σの範囲内にデータが収まる確率を意味します。この範囲を使用して、信頼区間を計算します。
信頼区間の範囲は以下の式で求められます。
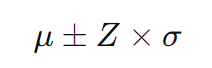
具体的には、
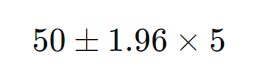
これを計算すると、信頼区間の範囲は次のようになります。
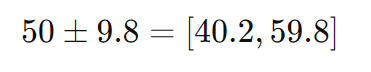
コインの枚数は整数なので、この範囲を四捨五入します。よって、95%の信頼区間は以下の範囲になります。
重回帰分析における信頼区間
重回帰分析(じゅうかいきゃくせき、Multiple Regression Analysis)は、複数の独立変数が従属変数に与える影響を分析する手法です。この分析の結果として得られるのが、各独立変数の回帰係数です。これらの回帰係数は、各変数が従属変数にどのように影響するかを示す重要な値です。しかし、この係数自体は「推定値」にすぎないため、実際の母集団における真の値がどれくらいの範囲にあるのかを知る必要があります。
ここで役立つのが信頼区間です。重回帰分析では、各回帰係数に対して信頼区間を設定し、その範囲内に真の回帰係数が存在する確率が高いことを示します。
信頼区間の意味
重回帰分析の結果として得られる信頼区間は、次のような質問に答えるのに役立ちます:
- 「この独立変数が従属変数に与える影響は、どの程度確実だろうか?」
- 「推定された回帰係数が、真の母集団における係数にどれだけ近いのか?」
例えば、ある独立変数 Xが従属変数 Yに与える影響を分析したとき、回帰係数が1.5であり、その信頼区間が[1.0, 2.0]だったとします。これは、「95%の確率で、Xの真の影響力は1.0から2.0の間にある」と解釈できます。
信頼区間の計算方法
重回帰分析における信頼区間は、次のステップで計算されます:
- 点推定値(回帰係数)の計算
重回帰分析の結果として得られる回帰係数が点推定値になります。 - 標準誤差の計算
各回帰係数に対応する標準誤差を計算します。標準誤差は、推定された回帰係数の不確実性の指標です。 - 信頼区間の幅の計算
先ほどの例と同様に、信頼区間の幅は標準誤差に信頼度に対応する値(通常はt値)を掛けたものです。 - 信頼区間の計算
回帰係数から信頼区間の幅を引いたものが下限、加えたものが上限となります。

信頼区間の解釈
信頼区間は、回帰分析の結果を正しく解釈するために非常に重要です。以下のポイントを押さえておくと良いでしょう:
- 信頼区間が0を含む場合
特定の独立変数の信頼区間が0を含む場合、その変数が従属変数に対して有意な影響を与えていない可能性があります。これは、独立変数が従属変数に影響を与えない(回帰係数が0)場合を示すからです。 - 信頼区間が狭い場合
信頼区間が狭い場合、その回帰係数の推定が精度高く行われていることを意味します。つまり、真の回帰係数が推定値に非常に近い可能性が高いということです。 - 信頼区間が広い場合
一方で、信頼区間が広い場合は、推定された回帰係数に対する不確実性が大きいことを示します。この場合、追加のデータを収集したり、モデルを改良する必要があるかもしれません。
具体的な例
例えば、以下のような重回帰分析の結果が得られたとします:
| 変数名 | 回帰係数 | 標準誤差 | 信頼区間(95%) |
|---|---|---|---|
| X1 | 1.5 | 0.25 | [1.0, 2.0] |
| X2 | -0.8 | 0.5 | [-1.8, 0.2] |
この例では、X1の信頼区間は[1.0, 2.0]なので、1.5という推定値は比較的精度が高く、X1が従属変数に対して正の影響を与えることがわかります。一方で、X2 の信頼区間は[-1.8, 0.2]であり、0を含んでいるため、X2が従属変数に与える影響は不確実です。これは、X2の効果があまり有意でないことを示唆しています。
信頼区間を活用するために
重回帰分析における信頼区間は、結果の信頼性を評価するための重要な指標です。これを正しく解釈することで、モデルの精度や変数の有意性についてより深い洞察を得ることができます。
今後は、重回帰分析の仮説検定やモデルの選択基準など、より高度なテーマに進むと、信頼区間の重要性がさらに理解できるようになるでしょう。また、実際にデータを使って分析を行い、得られた信頼区間の解釈を練習することもお勧めします。
まとめと今後の学習の指針
今後は、信頼区間を用いた他の確率的な予測方法や、異なる試行回数の場合の変化についても学んでみてください。
投稿者プロフィール

- 代表取締役
-
セイ・コンサルティング・グループ株式会社代表取締役。
岐阜県出身。
2000年創業、2004年会社設立。
IT企業向け人材育成研修歴業界歴20年以上。
すべての無駄を省いた費用対効果の高い「筋肉質」な研修を提供します!
この記事に間違い等ありましたらぜひお知らせください。
学生時代は趣味と実益を兼ねてリゾートバイトにいそしむ。長野県白馬村に始まり、志賀高原でのスキーインストラクター、沖縄石垣島、北海道トマム。高じてオーストラリアのゴールドコーストでツアーガイドなど。現在は野菜作りにはまっている。

