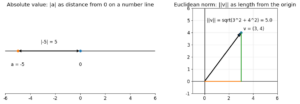
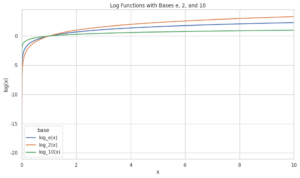
【線形代数】あの「串刺し団子」みたいな記号は何？「Φ（ファイ）」の使い方を徹底解説

2026年1月9日 2026年1月9日山崎講師

山崎講師

こんにちは。ゆうせいです。

数学の教科書を開くと、アルファベットに混じって「ギリシャ文字」がたくさん出てきますよね。

$\alpha$ （アルファ）や $\beta$ （ベータ）くらいならまだ可愛いものですが、読み方すら自信がない記号が出てくると、そこで思考が停止してしまいませんか？

今回解説するのは、丸に縦棒が突き刺さったような記号、「 $\phi$ （ファイ）」です。

「これ、物理だと磁束とかで見たことあるけど、線形代数だと何なの？」

「空集合の記号と似てるけど、同じもの？」

そんな疑問を持っている新人エンジニアのみなさんに、線形代数や機械学習の文脈でこの記号がどう使われているのか、その正体をやさしく解説します。

実はこの記号、文脈によって「変身」するカメレオンのようなやつなんです。

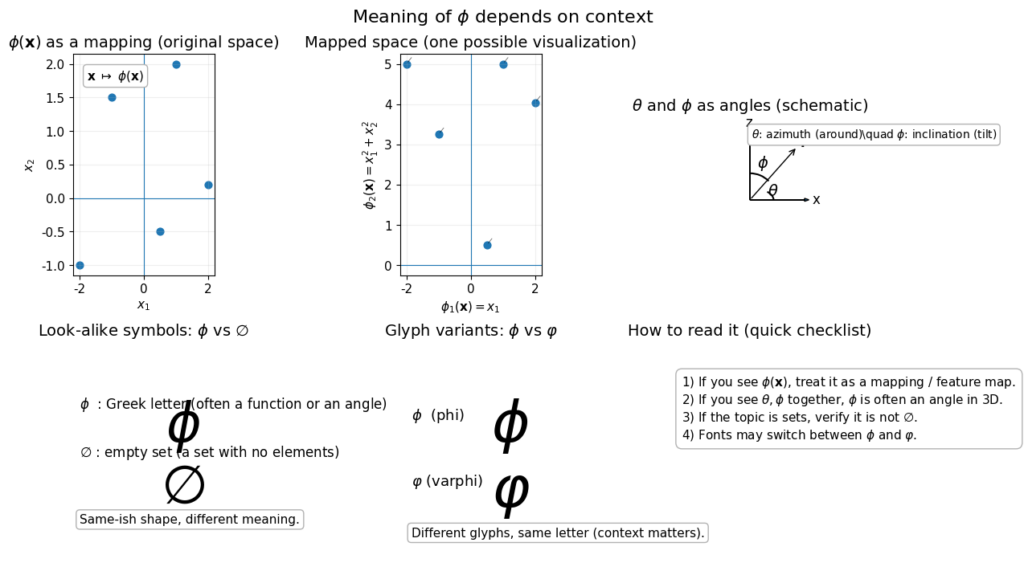
1. 最も多い使われ方：変身させる「関数（写像）」

線形代数の本や、機械学習の論文で $\phi(x)$ という形で出てきたら、十中八九これです。

$\phi$ は、「ベクトルを別の形に変身させる装置（関数・写像）」を表す記号としてよく使われます。

なぜ「f」じゃないの？

数学で関数といえば $f(x)$ が定番ですよね。

でも、線形代数では「ある空間から、別の空間へ移動させる」というニュアンスを強調したいときに、あえてギリシャ文字を使う習慣があります。

前回の記事で解説した「カーネル法」を思い出してください。

2次元のデータを、無限次元の空間へワープさせる「特徴写像」がありましたよね？

あのとき、データを変換する関数のことを $\phi(\mathbf{x})$ と書きました。

$f(x)$ ：数値を計算して答えを出すイメージ。
$\phi(\mathbf{x})$ ：空間ごと移動させる、構造を変えるイメージ。

エンジニアとしては、

「おっ、 $\phi$ が出てきたな。データを別の次元や別の空間にマッピング（変換）しようとしているんだな」

と読み取ればOKです。

2. 角度を表す「ファイ」

次は、幾何学的な意味での使い方です。

ベクトルといえば「向き」と「大きさ」ですよね。この「向き（角度）」を表すときにも $\phi$ が登場します。

「えっ、角度って $\theta$ （シータ）じゃないの？」

と思いましたか？その通りです。基本はシータを使います。

しかし、3次元空間（ $x, y, z$ ）になると、角度が1つでは足りません。

そこで、2つ目の角度として $\phi$ が助っ人に呼ばれるのです。

$\theta$ （シータ）：横方向の回転（経度のようなもの）
$\phi$ （ファイ）：縦方向の傾き（緯度のようなもの）

ロボットアームの制御や、3Dグラフィックスのカメラ位置を計算するときには、この「シータとファイのコンビ」が頻繁に登場します。

3. 注意！「空集合」とは別物です

ここで、新人エンジニアが一番ハマりやすい罠についてお話しします。

数学には、「中身が何もない空っぽの集合」を表す「空集合（くうしゅうごう）」という概念があります。

この記号、 $\emptyset$ （丸に斜め線）と書くのですが、手書きだと $\phi$ （丸に縦線）とそっくりなんです！

$\phi$ （ファイ）：ギリシャ文字。関数や角度に使われる。縦線または少し斜め。
$\emptyset$ （空集合）：ノルウェー語などのアルファベットが由来。数字の0に斜線を引いた形。

これらはまったくの別物です。

プログラミングで言うなら、「関数（Function）」と「Null（値なし）」くらい違います。

線形代数の文脈で「変換」の話をしているのか、集合論の文脈で「要素なし」の話をしているのか、前後の文脈から見極める必要があります。

メリットとデメリット

このように、文脈によって意味が変わる記号を使うことには、良い点と悪い点があります。

メリット

役割分担ができる：普通の関数 $f$ と、空間を変える写像 $\phi$ を使い分けることで、数式の意味（ニュアンス）を伝えやすくなります。
慣習として通じやすい：物理学や工学の長い歴史の中で「角度やポテンシャルといえばファイ」という共通認識があるため、専門家同士では話が早いです。

デメリット

初見殺しである：「ファイ＝これ！」という決まった定義がないため、教科書の最初のページ（定義集）を確認しないと、何を指しているのかわからないことがあります。
フォントの罠：パソコンのフォントによって、 $\phi$ （丸に縦棒）だったり、 $\varphi$ （一筆書きのような丸い形）だったりと、見た目が変わることがあります。これらは同じ文字の「書体の違い」に過ぎませんが、初心者を混乱させる原因になります。

まとめ：文脈を読む探偵になろう

ここまで読んでいただき、ありがとうございます。

謎の記号 $\phi$ の正体、少し見えてきましたか？

関数（写像）：データを別の空間へ飛ばす装置。
角度： 3次元空間での2つ目の角度。
空集合：形は似ているけど赤の他人。

線形代数、特に機械学習の分野で $\phi$ が出てきたら、まずは「特徴写像（データを変換する関数）」ではないかと疑ってみてください。9割方、その読みで正解です。

数式の中のギリシャ文字は、ただの「記号」ではなく、その変数の「役割」を表す名札のようなものです。

怖がらずに、「今回はどんな役回りで登場したのかな？」と探ってみてくださいね。

今後の学習の指針

さて、データを変換する $\phi$ の話が出たところで、次は「固有値（Eigenvalue）」と「固有ベクトル（Eigenvector）」について学んでみるのはいかがでしょうか。

「ある変換 $\phi$ をしても、向きが変わらない特別なベクトルがある」

という、線形代数の中でもトップクラスに面白く、そして重要な概念です。

これを理解すると、Googleの検索アルゴリズムの仕組みなんかもわかるようになりますよ。

それでは、また次回の記事でお会いしましょう！

セイ・コンサルティング・グループの新人エンジニア研修のメニューへのリンク

投稿者プロフィール

山崎講師代表取締役

セイ・コンサルティング・グループ株式会社代表取締役。
岐阜県出身。
2000年創業、2004年会社設立。
IT企業向け人材育成研修歴業界歴20年以上。
すべての無駄を省いた費用対効果の高い「筋肉質」な研修を提供します！
この記事に間違い等ありましたらぜひお知らせください。

学生時代は趣味と実益を兼ねてリゾートバイトにいそしむ。長野県白馬村に始まり、志賀高原でのスキーインストラクター、沖縄石垣島、北海道トマム。高じてオーストラリアのゴールドコーストでツアーガイドなど。現在は野菜作りにはまっている。