【機械学習の国境線】白黒つける「決定境界」とは？ロジスティック回帰が引く“運命のライン”
山崎講師こんにちは。ゆうせいです。
テストの結果が返ってくるとき、「60点以上が合格」と言われたら、59点と60点の間には天と地ほどの差がありますよね。
たった1点の違いで、「合格者」になるか「不合格者」になるかが決まってしまう。
機械学習の分類問題（例えば、スパムメールかどうかを判定するAI）でも、これと同じことが起きています。
データの世界には、AチームとBチームを分ける「見えない壁」が存在しているのです。
その壁の名前こそが、今回解説する「決定境界（Decision Boundary）」です。
前回、ロジスティック回帰が「実は直線を引いている」という話をしましたよね。
今日は、その直線が具体的にどのような役割を果たし、データの運命をどう分けているのかを解説します。
これを知れば、AIがどのような基準で「判定」を下しているのかが、手にとるようにわかるようになりますよ。
決定境界とは「運命の分かれ道」
決定境界とは、一言で言えば「データを分類するための境界線」のことです。
イメージしてください。
地面にたくさんの「赤いボール」と「青いボール」が散らばっています。
あなたは長い棒を一本持っていて、それを地面に置くことで、赤と青をきれいに分けたいと思います。
「この棒より右側は全部『赤』！」
「左側は全部『青』！」
このように宣言したとき、あなたが置いたその棒こそが「決定境界」です。
新しいボールが転がってきたとき、そのボールが棒の右にあるか左にあるかだけで、
「君は赤チームだね」
「君は青チームだね」
と瞬時に判定できるようになります。
ロジスティック回帰における決定境界
では、前回学んだロジスティック回帰では、この線はどこに引かれるのでしょうか？
答えはズバリ、「確率が50%（0.5）になる場所」です。
数式で見る「国境」の場所
ロジスティック回帰では、確率 
ここで、前回の「ロジット（対数オッズ）」を思い出してみましょう。
確率 
オッズ
オッズは「1倍」になります。勝ちと負けが五分五分の状態ですね。
では、このオッズ（1）の対数（ロジット）をとると？
ロジット
そうです、「0」になります！
対数の世界で「0」は真ん中を意味します。
そして、ロジットは 
つまり、決定境界の方程式はこうなります。
なんと！ 中学校で習った「一次方程式（ 
ロジスティック回帰は、確率というフワッとしたものを計算していますが、最終的に白黒つけるためのラインは、「
次元が変われば「線」も変わる
「決定境界」という名前ですが、いつも「線」とは限りません。データの複雑さ（次元）によって、その姿を変えます。
- 1次元（変数が1つ）の場合：テストの点数（
）だけで合否を決める場合。決定境界は数直線上の「点」（例：60点の位置）になります。
- 2次元（変数が2つ）の場合：身長と体重でサイズを決める場合。決定境界は平面上の「直線」になります。私たちが一番イメージしやすいのはこれです。
- 3次元以上（変数がたくさん）の場合：年齢、年収、住所…と変数が3つ以上ある場合。決定境界は空間を分ける「平面」、あるいはもっと高次元の「超平面（Hyperplane）」になります。
エンジニアとしては、「変数の数が増えても、結局は空間をスパッと切断する壁があるんだな」とイメージできればOKです。
線形 vs 非線形：ぐにゃぐにゃした境界線
ここまでは「真っ直ぐな線（線形）」の話をしてきましたが、世の中には直線では分けられないデータもたくさんあります。
例えば、赤チームが真ん中に固まっていて、その周りを青チームがドーナツ状に取り囲んでいる場合。
これを一本の直線で分けるのは無理ですよね？
こういうときは、決定境界をぐにゃぐにゃと曲げる必要があります。これを「非線形（ひせんけい）の決定境界」と呼びます。
- ロジスティック回帰（基本）：直線の境界しか引けません。
- サポートベクターマシン（カーネル法）やニューラルネットワーク：ぐにゃぐにゃした曲線の境界を引くことができます。
ディープラーニングがすごいと言われる理由は、この「決定境界を自由自在に折り曲げて、どんな複雑な分布でもきれいに切り分けることができる」からなんです。
注意点：複雑ならいいってものじゃない？
「じゃあ、複雑な線が引けるモデル最強じゃん！」と思いますよね？
ここに「過学習（Overfitting）」という落とし穴があります。
決定境界をぐにゃぐにゃにしすぎて、たまたま紛れ込んでいたノイズ（外れ値）まで丁寧に分けようとすると、境界線がいびつな形になってしまいます。
すると、新しいデータが来たときに、かえって間違った判定をしてしまうのです。
「シンプルイズベスト」な直線（ロジスティック回帰）の方が、結果的に安定して高スコアを出すこともよくあるんですよ。
まとめ：AIは「線引き」をしているだけ
ここまで読んでいただき、ありがとうございます。
決定境界の正体、見えましたか？
- 決定境界とは、データを分類する「壁」。
- ロジスティック回帰の場合、その壁は 「
」 というシンプルな形になる。
- 確率 0.5 の場所が、まさにその壁の位置である。
- 複雑に曲がった境界線を作ることもできるが、やりすぎ（過学習）には注意。
結局のところ、多くのAIモデルがやっていることは、
「データをきれいに分けるためには、どこに線を引けばいいの？」
というお絵かき問題を、必死に計算して解いているだけなのです。
今後の学習の指針
さて、線を引くとなると、「どの位置に引くのが一番いいのか？」という疑問が湧いてきませんか？
ギリギリを攻めるのか、余裕を持って真ん中に引くのか。
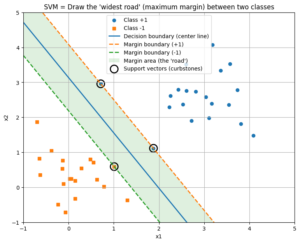
この「線の引き方の美学」を追求したのが、「サポートベクターマシン（SVM）」という手法です。キーワードは「マージン最大化」。
「一番太い道路を通す」というカッコいい考え方なので、ぜひ次はこれを調べてみてください。
それでは、また次回の記事でお会いしましょう！
セイ・コンサルティング・グループの新人エンジニア研修のメニューへのリンク
投稿者プロフィール
