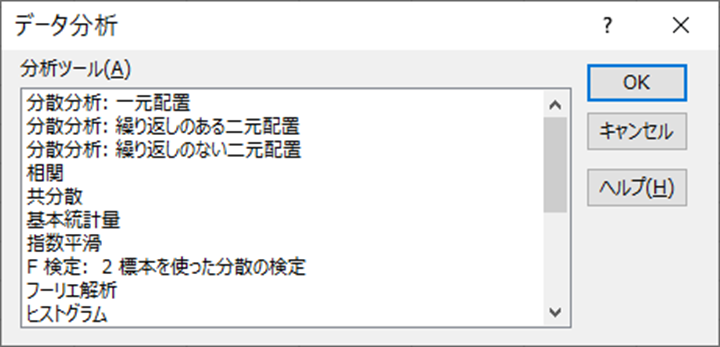
エクセルの「データ分析」アドオンで利用できる主要な機能

2024年10月30日 最終更新日時 : 2024年10月30日 山崎講師山崎講師

エクセルの「データ分析」アドオンで利用できる主要な機能について、それぞれの特徴や活用例を解説します。データ分析ツールは、統計的分析を初心者にもわかりやすく実施できる便利なツールです。具体的な機能の一つひとつについて、使い方や理解を深めるための説明をしていきます。

分散分析（ANOVA）：一元配置

「分散分析：一元配置」は、複数のグループ間での平均値の差が統計的に有意かどうかを検定する方法です。たとえば、複数の授業で異なる指導法を用いた場合に、成績に差があるかを調べる際に使います。

  • 用途例：複数の実験グループ間での効果の違いを調べたいとき
  • メリット：複数グループ間での比較が可能
  • デメリット：二つのグループ間のみに適しているわけではなく、どのグループで差があるかは特定できない

分散分析：繰り返しのある二元配置

「分散分析：繰り返しのある二元配置」は、2つの要因の影響を同時に評価し、それぞれがデータにどのように影響しているかを調べる手法です。「繰り返し」とは、同じ条件下で複数回実験が行われることを意味します。

  • 用途例：例えば、「異なる肥料」と「異なる温度条件」が植物の成長に与える影響を調べるとき
  • メリット：要因の相互作用も評価可能
  • デメリット：実験の計画とデータ収集が複雑

分散分析：繰り返しのない二元配置

「分散分析：繰り返しのない二元配置」は、二つの要因がデータに与える影響を同時に評価するが、繰り返しがない場合に用いる手法です。要因間の相互作用や独立の影響を調べることが可能です。

  • 用途例：異なる教科と指導法の組み合わせが学力に与える影響を調べるとき
  • メリット：複数要因の影響を同時に分析できる
  • デメリット：繰り返しデータがないため、データの変動をうまく捉えられないことがある

相関

「相関」は、2つの変数がどの程度互いに関係しているかを示す指標です。相関係数は-1から1の範囲で、1に近いほど強い正の関係、-1に近いほど強い負の関係を示します。

  • 用途例：気温とアイスクリームの売上の関係を分析
  • メリット：関係性の強さと方向を簡単に把握
  • デメリット：因果関係ではなく、相関関係のみを示す

共分散

「共分散」は、2つの変数がどの程度同じ方向に動くかを示す指標です。正の値なら同じ方向に動き、負の値なら逆方向に動く傾向があることを表します。

  • 用途例：株式のリターン同士の動きを分析し、ポートフォリオのリスクを評価
  • メリット：相関の方向性が分かる
  • デメリット：数値が大きすぎたり小さすぎたりして比較が難しい

基本統計量

「基本統計量」は、平均、分散、標準偏差、最大値、最小値など、データの基礎的な情報をまとめて計算する機能です。

  • 用途例：顧客の年齢分布などの基本情報を得たいとき
  • メリット：データの概要を迅速に把握可能
  • デメリット：データの全体像のみで詳細な分析には向かない

指数平滑

「指数平滑」は、過去のデータを基に将来の値を予測するための方法で、特に売上予測などの時系列データで利用されます。

  • 用途例：売上データから次月の売上を予測
  • メリット：最近のデータを重視した予測が可能
  • デメリット：トレンドが変わると予測精度が低下する

F検定: 2標本を使った分散の検定

「F検定」は、2つのグループの分散が等しいかどうかを調べるための手法です。分散の差が有意であれば、異なる集団とみなされます。

  • 用途例：薬の効果に関する実験で、治療群と対照群のデータのばらつきが異なるか確認
  • メリット：分散の等しさを検定可能
  • デメリット：正規分布を仮定するため、データの分布に依存する

フーリエ解析

「フーリエ解析」は、波のような周期的なデータを周波数成分に分解する手法です。音声データの分析や振動解析で使用されます。

  • 用途例：音楽信号の解析や、振動データの解析
  • メリット：複雑な波形を分解し、各周波数成分を明確にできる
  • デメリット：データが周期的でない場合には適用が難しい

ヒストグラム

「ヒストグラム」は、データの分布を視覚化するための棒グラフで、データがどの範囲にどれだけ分布しているかを確認できます。

  • 用途例：学生のテストの点数分布を可視化
  • メリット：データの分布が一目でわかる
  • デメリット：棒の幅によって印象が変わる

移動平均

「移動平均」は、時系列データの変動を平滑化し、トレンドを把握しやすくする手法です。株価や売上データでよく使われます。

  • 用途例：株価のトレンドを分析
  • メリット：短期的なノイズを除去し、長期的な傾向を把握しやすい
  • デメリット：遅れが生じ、迅速な変化には対応できない

乱数発生

「乱数発生」は、特定の範囲でランダムな数値を生成する機能で、シミュレーションやモンテカルロ法に利用されます。

  • 用途例：シミュレーション実験
  • メリット：再現性のある乱数生成が可能
  • デメリット：ランダム性が真のランダムとは異なる場合がある

順位と百分位数

「順位と百分位数」は、データの順位や、全体の中での位置（百分率）を計算する機能です。成績の位置づけに使用されます。

  • 用途例：テストのスコアを上位何パーセントか評価
  • メリット：個々のデータの相対的な位置がわかる
  • デメリット：データ数が少ないと精度が低下する

回帰分析

「回帰分析」は、変数間の関係をモデル化し、予測を行うための手法です。売上と広告費の関係などで活用されます。

  • 用途例：広告費を基に売上を予測
  • メリット：因果関係の推定が可能
  • デメリット：関係が線形でない場合に適用が難しい

サンプリング

**「

サンプリング」**は、大量のデータから代表的なサンプルを抽出する方法で、アンケート調査や実験で使用されます。

  • 用途例：顧客全体の満足度を少数のサンプルから評価
  • メリット：効率よく代表性のあるデータを得られる
  • デメリット：サンプルの偏りがあると全体の結果に影響

t検定：一対の標本による平均の検定

「t検定（ペア）」は、同じ対象が2つの条件でどれほど異なるかを調べる方法です。前後の効果を比較する際に適しています。

  • 用途例：新しい指導法を前後で評価
  • メリット：同じ個体での差を測定可能
  • デメリット：データが対になっていることが前提

t検定：等分散を仮定した2標本による検定

「t検定（等分散）」は、2つの独立した集団の平均の差があるかを調べます。分散が等しい場合に適用されます。

  • 用途例：2つのグループの平均的なパフォーマンスの差を検証
  • メリット：簡単にグループ間の比較ができる
  • デメリット：分散が等しくない場合、誤差が生じる

t検定：分散が等しくないと仮定した2標本による検定

「t検定（分散不等）」は、2つの独立した集団の平均の差があるかを調べるが、分散が異なる場合に適用します。

  • 用途例：異なる条件で行われた実験結果の比較
  • メリット：分散の違いを考慮した検定が可能
  • デメリット：標本数が少ないと精度が落ちる

z検定：2標本による平均の検定

「z検定」は、2つの集団の平均に差があるかを検定する方法で、データ数が多い場合に使用されます。

  • 用途例：異なる学校の平均点の差を検証
  • メリット：大きなデータセットで信頼性の高い結果が得られる
  • デメリット：サンプル数が少ない場合には不向き

これらのツールを使うことで、エクセルで統計分析が容易になります。次のステップとしては、実際にデータを入力しながら、各機能の結果を検証してみることをおすすめします。

投稿者プロフィール

山崎講師
山崎講師代表取締役
セイ・コンサルティング・グループ株式会社代表取締役。
岐阜県出身。
2000年創業、2004年会社設立。
IT企業向け人材育成研修歴業界歴20年以上。
すべての無駄を省いた費用対効果の高い「筋肉質」な研修を提供します！
この記事に間違い等ありましたらぜひお知らせください。
対象読者
全ての社員
前の記事
フレーミングと営業トークとは？ 〜IT営業を例に〜
2024年10月27日
次の記事
ログインなしでMiroを使うための手順と注意点
2024年10月30日