初心者にもわかる！グラフ理論とは何か？】

2025年7月31日 2025年7月31日山崎講師

山崎講師

こんにちは。ゆうせいです。
今回は「グラフ理論（Graph Theory）」について、数学が苦手な方でも理解できるように、丁寧に噛み砕いて解説します！

ざっくり言うと？

グラフ理論とは、「点」と「線」を使ってモノとモノの関係を表す数学の分野です。

これを使うと、人間関係、道路網、インターネット、SNS、配送経路、分子構造など、
「モノ同士のつながり」をモデル化・分析できます。

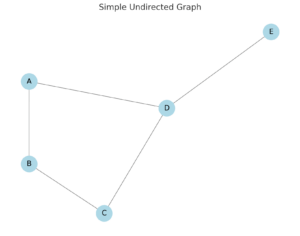
図で見るとわかりやすい！

点（ノード、頂点）：人、都市、ウェブページなど
線（エッジ、辺）：関係、道、リンクなど

次のような形になります：

A --- B --- C
 \         /
  \       /
   \     /
     D

このような構造をグラフ（graph）と呼びます！

グラフ理論で扱う基本用語

用語	意味
頂点（vertex）	点、ノード（人や場所など）
辺（edge）	頂点同士のつながり、リンク、線など
有向グラフ	辺に方向がある（例：A → B）
無向グラフ	辺に方向がない（例：A — B）
重み（weight）	各辺に付けられた値（距離、コストなど）
次数（degree）	各頂点につながっている辺の数

たとえ話で理解しよう！

例①：友だち関係（SNS）

各人が「頂点」
友だち登録が「辺」

→ 誰と誰がつながっているかをグラフで表すと、コミュニティの構造が見えてきます！

例②：道路ネットワーク

都市が「頂点」
道路が「辺」
距離が「重み」

→ 最短経路を探すアルゴリズム（ナビ）に応用！

どんなことができるの？

応用シーン	内容例
最短経路探索	地図アプリ、配達ルートの最適化
ネットワーク分析	SNSの影響力分析、ウイルスの感染経路解析
クラスタリング	コミュニティ検出、話題のグループ分け
巡回セールスマン問題	最も効率的に都市を回るルートを求める
電気回路・交通・通信網	インフラ設計やリスク管理など多分野で活用されている

有名な問題例

● オイラー路問題（橋を一筆書きできるか？）

18世紀、ケーニヒスベルクの7つの橋を「一度だけ渡ってすべての橋を通ることは可能か？」
→ グラフ理論の原点！

● ダイクストラ法

最短経路を求めるアルゴリズム。今のGoogleマップにも応用されています。

数学的にはどう表される？

グラフは以下のように定義されます：

$G = (V, E)$

$V$：頂点の集合（Vertices）
$E$：辺の集合（Edges）

場合によっては「重み」も含めて $G = (V, E, w)$ と書かれることもあります

まとめ

グラフ理論とは？	点と線で「関係性」を表す数学モデル
扱うもの	頂点、辺、重み、有向／無向など
できること	最短経路、ネットワーク解析、構造分析など

今後の学習のヒント

グラフ理論をさらに深く学ぶためには、以下のトピックがオススメです！

有向グラフとDAG（有向非巡回グラフ）
探索アルゴリズム（DFS、BFS）
最短経路（ダイクストラ法、ベルマンフォード法）
グラフ構造と行列（隣接行列、ラプラシアン行列）
現代応用：知識グラフ、グラフニューラルネットワーク（GNN）

興味のあるテーマがあれば、ぜひ教えてください！一緒に学びましょう！

生成AI研修のおすすめメニュー

投稿者プロフィール

山崎講師代表取締役

セイ・コンサルティング・グループ株式会社代表取締役。
岐阜県出身。
2000年創業、2004年会社設立。
IT企業向け人材育成研修歴業界歴20年以上。
すべての無駄を省いた費用対効果の高い「筋肉質」な研修を提供します！
この記事に間違い等ありましたらぜひお知らせください。