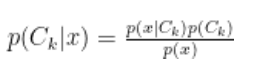新入社員
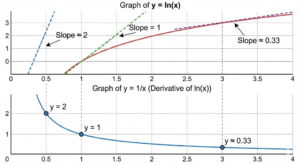
【新人エンジニア研修】対数の微分がなぜ分数になるのか?直感と論理で教える技術
こんにちは。ゆうせいです。 新人エンジニアの研修を担当されているみなさん、毎日の講義お疲れ様です。講義の中で、数学的な概念を説明しなければならない場面に出くわすことはありませんか。 たとえば、アルゴリズムの計算量やデータ […]
「感情」が記憶のカギ?海馬と扁桃体をハックして技術を定着させる脳科学的アプローチ
こんにちは。ゆうせいです。 新しいプログラミング言語や技術書を読んでいるとき、どうしても内容が頭に入ってこないことはありませんか? 「自分は記憶力が悪いんだ」と諦めるのはまだ早いです。実は、脳の仕組みをうまく利用できてい […]
暗記が苦手でも大丈夫!エンジニアが知るべき「脳と記憶」の仕組み
こんにちは。ゆうせいです。 一生懸命勉強したプログラミング言語の構文なのに、翌日にはすっかり忘れてしまって落ち込むことはありませんか?一方で、子供の頃に覚えた自転車の乗り方は、何年乗っていなくても忘れませんよね。 なぜこ […]
データ分析の第一歩!コイン投げから学ぶベルヌーイ分布と二項分布の仕組み
こんにちは。ゆうせいです。 新人エンジニアのみなさん、データ分析や機械学習という言葉を聞いて、なんだか難しそうだと身構えていませんか。数式がたくさん出てくると、どうしても頭が痛くなってしまうかもしれませんね。 でも、安心 […]
生成モデル、識別モデル、識別関数の違い
AIの世界へようこそ! 機械学習を学び始めると、「モデル」という言葉が何度も出てきますよね。 特にE資格でも重要なのが、データをどう扱うかというスタンスの違いである「生成モデル」「識別モデル」「識別関数」の3つです。 こ […]
AIが賢くなる秘密の数式?ベイズの定理で「データから正解」を導き出す方法
こんにちは。ゆうせいです。 新人エンジニアのみなさん、AIが「この画像は 80% の確率で猫だ!」と判断するとき、裏側でどんな計算が行われているか知っていますか。 その核心にあるのが、統計学の超重要ルールであるベイズの定 […]
【NumPy応用】乱数を操る!choiceとshuffleを使いこなして脱・初心者を目指そう
こんにちは。ゆうせいです。 前回の記事では、NumPyの乱数生成の基本である「3つの神器(rand, randn, randint)」と、再現性を保つための「シード値」についてお話ししました。 「サイコロを振る」ような単 […]
【完全攻略】Axis=0と1の呪いを解く!「縦か横か」迷わなくなる直感的イメージ法
こんにちは。ゆうせいです。 Pythonでデータ分析を始めて、pandasやNumPyを使い始めた新人エンジニアのみなさん。必ず一度は頭を抱える「ある問題」がありますよね。 そう、「Axis(アクシス)問題」です。 df […]
【初心者必見】合成関数の微分とは?「外側×内側」のルールを新人エンジニア向けに完全解説
こんにちは。ゆうせいです。 新人エンジニアのみなさん、ディープラーニングや機械学習の参考書を読んでいて、突然現れる複雑な数式に頭を抱えていませんか。とくに「誤差逆伝播法」のようなカッコいい名前の技術を学ぼうとすると、必ず […]
【初心者向け】最小二乗法とは?数式の意味から求め方まで新人エンジニアのために徹底解説
こんにちは。ゆうせいです。 新人エンジニアのみなさん、データの分析や機械学習の勉強を始めたときに、最初にぶつかる壁は何でしょうか。そう、数式ですよね。とくに、回帰分析などの基礎として登場する最小二乗法という言葉を聞いて、 […]
高校数学で挫折した「log(ログ)」が、AI開発の救世主だった話
こんにちは。ゆうせいです。 「サイン、コサイン、何になる?」なんて言葉がありますが、それ以上に「これ、人生でいつ使うの?」と思われがちなのが、高校数学で習う「対数(log、ログ)」ではないでしょうか。 この記号を見ただけ […]
確率と尤度の違いを「時間の矢」で攻略!未来の予測と過去の推理
こんにちは。ゆうせいです。 新人エンジニアのみなさん、統計学や機械学習の勉強をしていて「尤度(ゆうど)」という言葉に出会ったことはありませんか? 「確率はなんとなくわかるけれど、尤度ってなんだろう?」「確率と同じじゃない […]
20代エンジニア必見!年金は死ぬまでもらえる?マクロ経済スライドの仕組みを徹底解説
こんにちは。ゆうせいです。 新人エンジニア研修の講師をしていると、技術の話だけでなく、将来のお金の話について相談されることがよくあります。みなさんは、給与明細を見るたびに引かれている厚生年金保険料を見て、こんなことを思っ […]
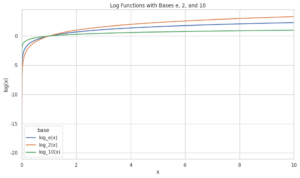
【数学の罠】「log」の底は10かeか2か?文脈で見分けるエンジニアのための生存戦略
こんにちは。ゆうせいです。 「数式に って書いてあるけど、これ、底(てい)はいくつなの?」 この悩み、エンジニアなら一度は必ず通る道です。 教科書やウェブサイトによって、底が省略されているときの正解が「2」だったり「10 […]
【線形代数】あの「串刺し団子」みたいな記号は何?「Φ(ファイ)」の使い方を徹底解説
こんにちは。ゆうせいです。 数学の教科書を開くと、アルファベットに混じって「ギリシャ文字」がたくさん出てきますよね。 (アルファ)や (ベータ)くらいならまだ可愛いものですが、読み方すら自信がない記号が出てくると、そこで […]
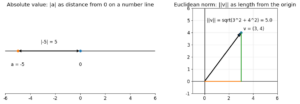
【数学の記号】その2本の棒は「ノルム」!ベクトルの「長さ」を測るメジャー
こんにちは。ゆうせいです。 このような質問をいただきました。 「絶対値記号のような2本の縦棒 は何ですか?」 鋭い質問ですね! 「絶対値の記号( )に似ているな」と思ったその感覚、大正解です。 あの2本の縦棒 の正体は、 […]
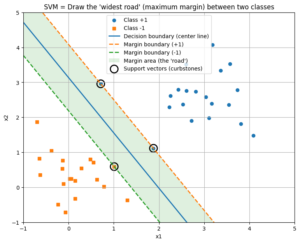
【機械学習】「SVM」はなぜ最強だったのか?データを分ける「一番太い道路」の引き方
こんにちは。ゆうせいです。 前回は、データを赤チームと青チームに分ける境界線、決定境界についてお話ししました。「確率0.5の場所に線を引く」というロジスティック回帰のアプローチでしたね。 しかし、ここで一つ問題があります […]
【機械学習の国境線】白黒つける「決定境界」とは?ロジスティック回帰が引く“運命のライン”
こんにちは。ゆうせいです。 テストの結果が返ってくるとき、「60点以上が合格」と言われたら、59点と60点の間には天と地ほどの差がありますよね。 たった1点の違いで、「合格者」になるか「不合格者」になるかが決まってしまう […]
【統計学の探偵】犯人は誰だ?「最尤推定」を新人エンジニアに直感的に解説
これまでの流れで、確率、オッズ、そしてロジスティック回帰の式の正体について解説してきました。 ここで新人エンジニアのみなさんに一つ、大きな疑問が生まれているはずです。 「式の形(モデル)はわかったけど、その中の具体的な数 […]
【ロジスティック回帰】「オッズ」の正体とは?確率を勝利の倍率に変換する数式ツアー
こんにちは。ゆうせいです。 みなさんは、競馬やスポーツベッティングなどの「ギャンブル」に興味はありますか? そこで必ず耳にする言葉がありますよね。そう、「オッズ」です。 「単勝オッズ 3.0倍!」 この言葉を聞くと、「勝 […]
AIの学習効率が劇的アップ!「誤差逆伝播法」は責任追求の伝言ゲーム
こんにちは。ゆうせいです。 前回は、AIがゴール(正解)に向かってパラメータを修正していく「勾配降下法」について学びました。 山を下るように、少しずつ誤差を減らしていくんでしたね。 しかし、ここで大きな問題があります。 […]
AIの学習は「山下り」!?勾配降下法で正解への最短ルートを探せ
こんにちは。ゆうせいです。 前回は、AIのテスト採点係である「損失関数」について学びました。 AIがどれくらい間違っているか、その誤差を「スコア」として算出する方法でしたね。 でも、ちょっと待ってください。 「あなたのス […]
AIはどうやって反省する?「損失関数」で誤差を数値化する仕組み
こんにちは。ゆうせいです。 前回は、AIに人間のような表現力を与える「活性化関数」についてお話ししました。 シグモイド関数を使って、データを確率(0から1の数字)に変換できるようになったわけです。 さて、ここで一つ質問で […]
AIの表現力が爆発!「活性化関数」とシグモイド関数の役割とは?
こんにちは。ゆうせいです。 前回は、AIの計算力を支える「行列の積」についてお話ししました。 データをまとめて計算する、いわば「工場のベルトコンベア」のような役割でしたね。 しかし、実はこのベルトコンベア(行列計算)を並 […]
機械学習の鬼門「行列の積」を攻略!データを一括処理する魔法の箱
こんにちは。ゆうせいです。 前回は、データ同士の相性を測る「内積」について解説しました。 「掛けて、足す」。このシンプルな計算が機械学習の基礎でしたね。 さて、今回はその内積をさらにパワーアップさせた「行列の積」について […]
機械学習の要「内積」を攻略!データ同士の「相性」を測る計算式
こんにちは。ゆうせいです。 前回は、データの大きさを1に揃える「単位ベクトル」についてお話ししました。 今回は、その単位ベクトルと切っても切れない関係にある、そして機械学習で最も頻繁に使われる計算の一つ、「内積(ないせき […]
機械学習の基礎!単位ベクトルとは?計算効率を上げる魔法の数字「1」の秘密
こんにちは。ゆうせいです。 みなさん、機械学習の勉強は進んでいますか。 エンジニアとしてデビューしたばかりの頃、「数学なんてライブラリがやってくれるから不要だろう」なんて思っていませんでしたか。実は私もそうでした。 でも […]
【新人エンジニア必見】線形代数の歴史を旅しよう!行列は誰がなぜ作ったの?
こんにちは。ゆうせいです。 みなさんは、数学と聞いてどんなイメージを持ちますか?もしかすると、学生時代の苦い思い出が蘇って、思わずブラウザを閉じようとした方もいるかもしれませんね。ちょっと待ってください! 実は、みなさん […]
【数学史】線形代数は何のために生まれた?元祖は「ツルとカメ」の計算だった
こんにちは。ゆうせいです。 前回は、線形代数が「まっすぐな世界を記号で解く」学問だというお話をしました。 では、そもそも昔の数学者たちは、なぜこんな面倒なルールを作り出したのでしょうか。学生を苦しめるため? いえいえ、違 […]
【数学コラム】線形代数ってなに?「まっすぐ」な世界を「記号」で解く物語
こんにちは。ゆうせいです。 エンジニアとして機械学習やデータ分析の勉強を始めると、必ず立ちはだかる大きな壁があります。 そう、 線形代数 です。 名前からして、なんだか堅苦しくて難しそうですよね。「線」はわかるけど、「形 […]